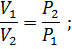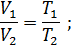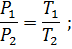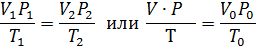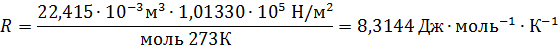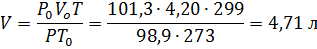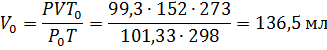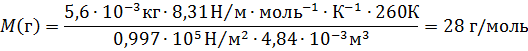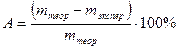Законы газового состояния. Определение молярных масс газообразных веществ



Три параметра – объем V, давление P и температура T (T=273+t) – определяют физическое состояние газа. Давление 1,013∙10 5 Па (760 мм рт. ст.) и температура 273 К или 0 о С называют нормальными условиями состояния газа, что в буквенных обозначениях этих величин указывается индексом: Po, To, to. Объем газа при н.у. – Vo.
Закон Бойля – Мариотта. При постоянной температуре объем данной массы газа изменяется обратно пропорционально давлению:
Закон Гей-Люссака. При постоянном давлении объем данной массы газа меняется прямо пропорционально абсолютной температуре
При постоянном объеме:
Уравнение Менделеева – Клапейрона. Объединение законов Бойля, Мариотта и Гей-Люссака дает уравнение состояния газа
если одно из состояний является нормальным. Для любого газа количеством вещества 1 моль величина 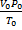
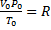
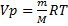
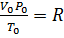
Если объем газа измерен в литрах, а давление газа в мегапаскалях (МПа=10 6 Па), то R=0,083л∙МПа∙моль -1 ∙К -1 . В расчетах обычно используют числа, имеющие три значащие цифры, что дает вполне достаточную точность: 22,4910 -3 м 3 , 22,4 л, 273 К, 8,31 Дж∙моль -1 ∙К -1 .
Согласно закону Авогадро, в равных объемах любых газов, взятых при одной и той же температуре и одинаковом давлении, содержится одинаковое число молекул.
Иными словами, одно и то же число молекул любого газа занимает при одинаковых условиях один и тот же объем. Вместе с тем 1 моль любого газа содержит одинаковое число молекул. Следовательно, при одинаковых условиях 1 моль любого газа занимает один и тот же объем. Этот объем называется мольным объемом газа и при нормальных условиях (0 0 С, давление 101,325 кПа) равен 22,4 л.
Пример 1.Определить объём, занимаемый 5,25 г азота при 26 0 С и давлении 98,9 кПа (742 мм рт.ст.).
Решение. Зная мольный объём и мольную массу (28,0 г/моль) азота, находим объём, который будут занимать 5,25 г азота при нормальных условиях:
28,0 г азота занимают объём 22,4л
5,25 г азота занимают объём VO ,
откуда VO = 5,25∙22,4/ 28,0 = 4,20 л
Затем приводим полученный объём к указанным в задаче условиям:
Пример 2.При25 0 С и давлении 99,3 кПа (745 мм рт.ст.) некоторое количество газа занимает объём 152 мл. Найти, какой объём займет это же количество газа при 0 0 С и давлении101,33 кПа.
Решение. Подставляя данные задачи в последнее уравнение, получаем:
Пример 3.Некоторый газ массой 5,6 г занимает объём 4,84 л притемпературе 17 0 С и давлении 0,997∙10 5 Па. Чему равна относительная молекулярная масса этого газа?
Решение. Из уравнения Менделеева-Клайперона 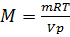
Так как числовое значение молярной массы, выраженной в г/моль, равно относительной молекулярной массе, т.е.
Источник
Методы определения молекулярных масс газообразных веществ
1. Метод измерения относительной плотности газа по газу
Относительной плотностью газа по газу называется отношение масс равных объемов газов, взятых при одинаковой температуре и давлении. Пусть mA и mB – массы равных объемов газов А и В. Тогда плотность газа А по газу В будет определяться следующим соотношением:
Молекулярная масса может быть определена, исходя из плотности газа по любому газу. На практике плотности газов обычно определяют либо по водороду, либо по воздуху. Соответственно,

где 29 – средняя молекулярная масса воздуха. Рассмотренный метод может быть применен и для определения молекулярных масс паров жидкостей.
2. Определение молекулярных масс по уравнению состояния идеального газа
Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона) имеет следующий вид:
где m — масса газа (г или кг), М – его молярная масса (г/моль или кг/моль), р – давление (Па или кПа), V – объем (м 3 или л), Т – абсолютная темепература (К), R – универсальная газовая постоянная (8,314 Дж/моль×К).
Поскольку при не слишком низких температурах и невысоких давлениях реальные газы удовлетворительно следуют данному уравнению, последнее можно использовать для определения молярных, а следовательно, и молекулярных масс газов. Для этого достаточно измерить при определенной температуре и давлении объем и массу газа, а затем рассчитать М по формуле
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Способы определения молярной массы газов
Существует ряд методов определения молекулярной массы газов при определенных внешних параметрах: давлении (Р), объеме (V) и температуре (Т).
1. По закону Авогадро и следствиям из него
Закон Авогадро: в равных объемах различных газов при одинаковых температуре и давлении содержится одинаковое число молекул.
Следствие 1: один моль любого вещества содержит количество структурных единиц данного вещества, равное постоянной Авогадро (Na = 6,02∙10 23 моль -1 ).
Следствие 2: при нормальных условиях (н.у.) (Р = 10 5 Па, Т = 273 К) один моль любого газа занимает объем 22,4 л. Эта величина получила название молярный объем (VM).
Зная массу m (г) какого-либо объема газа при н.у. и его объем V0 (л), можно рассчитать его молекулярную массу.
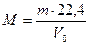 . . | (2.3.1) |
Следствие 3: массы равных объемов двух газов, взятых при одинаковых давлении и температуре, относятся друг к другу, как их молярные массы:
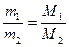 . . | (2.3.2) |
Отношение массы определенного объема первого газа к массе такого же объема второго газа (взятого при тех же условиях) называется относительной плотностью первого газа по второму (D). Тогда:
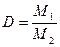 . . | (2.3.3) |
Обычно плотность газа определяют по отношению к водороду (DH2) или воздуху ( 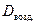
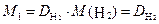 · 2, · 2, | (2.3.4) |
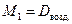 М возд.= М возд.= 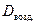 ·29. ·29. | (2.3.5) |
С учётом вышеуказанных условий для расчёта количества вещества используют следующие соотношения:
n 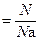 , , | (2.3.6) |
где N – количество структурных единиц в системе;
n 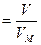 , , | (2.3.7) |
2. По уравнению Клапейрона – Менделеева
Если условия, в которых находится газ, отличны от нормальных, то параметры газа определяют по уравнению Клапейрона – Менделеева:
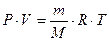 , , | (2.3.8) |
тогда молекулярную массу газа рассчитывают по формуле: 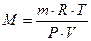 . . | (2.3.9) |
Единицы измерения величин в данном уравнении зависят от того, в каких единицах выражена масса (табл.1.2.1).
Источник
Определение молекулярной массы газообразных веществ



Цель работы: экспериментально определить молекулярную массу оксида углерода (IV).
Определение молярной массы газа может быть выполнено несколькими способами.
Чаще всего его определяют исходя из абсолютной и относительной плотности газов.
Абсолютной плотностью газа 
М = 22,4 ∙
Для приведения объёма, газа к нормальным условиям используют уравнение газового состояния
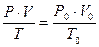
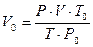
где V – объёма газа, измеренный при реальных условиях, т.е. при атмосферном давлении P и температуре Т.
Относительной плотностью D первого газа по второму называют отношение плотностей этих газов
D = 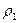
где 
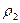
Это отношение можно заменить отношение масс газов, содержащихся в одинаковых объёмах при одинаковой температуре
D = 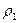
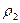
где m1 — масса первого газа,
По закону Авогадро в одинаковых объёмах любых газов при одних и тех же условиях содержится равное число молекул. Следовательно, их массы относятся друг к другу как их молярные массы
Так как m1 / m2 – плотность первого газа по второму, то
Молярную массу газа можно вычислить также, пользуясь уравнением Менделеева – Клайперона
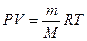
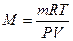
где P – давление, Па;
М – молярная масса, кг/моль;
R — молярная газовая постоянная, равная 8,314 Дж/(моль∙К);
Т – абсолютная температура, К.
Экспериментальная часть
Определение молекулярной массы оксида углерода (IV).
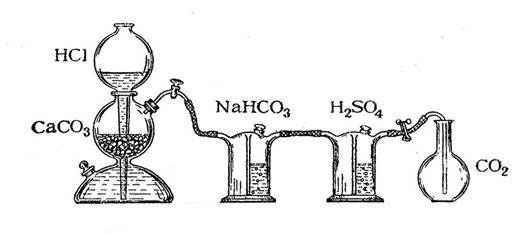
Определение молекулярной массы оксида углерода (IV) проводится в приборе, изображённом на рис.1. Оксид углерода (IV) получается в аппарате Киппа действием 10%-ой соляной кислоты на мрамор:
Оксид углерода (IV) подвергают очистке, пропуская последовательно через растворы NaHCO3 и H2SO4.
Рисунок 1. Аппарат Кипа
Взвесить колбу с пробкой на технохимических весах с точностью до 0,01г. Данные записать. Наполнить колбу оксидом углерода (IV), опустив газоотводную трубку до дна колбы. Закрыть колбу пробкой (пробка должна входить на ту же глубину, что при взвешивании колбы) и вновь взвесить. Чтобы быть уверенным в том, что воздух из колбы полностью вытеснен, и она целиком наполнена оксидом углерода (IV), надо, взвесив колбу, ещё раз на несколько минут опустить в неё газоотводную трубку, опустить и вновь взвесить колбу, повторяя эту операцию до получения постоянной массы колбы. Массу колбы с оксидом углерода (IV) записать. Определить объём колбы, наполнив её водой до пробки, затем измерить объём воды мерным цилиндром и записать результаты. Отметить и записать показания термометра и барометра во время опыта.
Форма записи наблюдений и обработка результатов.
| 1. | Масса колбы (с пробкой) с воздухом – m1, г |
| 2. | Масса колбы (с пробкой) с оксидом углерода (IV) – m2, г |
| 3. | Объём колбы – V, мл |
| 4. | Температура – t, 0 С |
| 5. | Давление – Р1, мм рт.ст. |
По полученным данным вычислить молекулярную массу оксида углерода (IV) с помощью уравнения Менделеева – Клапейрона, исходя из относительной плотности оксида углерода (IV) по водороду, если известно, что масса 1л Н2 при н.у. 0,09г.
В конце опыта вычислить относительную ошибку в процентах:
Вопросы и задачи.
1. Как следует формулировать закон Авогадро? Что показывает число Авогадро?
2. Что называется относительной плотностью газа?
3. Как можно вычислить молекулярную массу вещества, зная плотность его паров по воздуху?
4. Какова плотность по воздуху азота N2, хлора Сl2 и оксида углерода (II) СО?
5. Что тяжелее: сухой углекислый газ или равный объём того же газа, содержащего водяные пары?
6. Масса 1 л газа при нормальных условиях 1,43 г. Чему равна молекулярная масса газа?
7. Вычислить молекулярную массу газа, если относительную плотность его по воздуху равна 0,966.
8. Плотность газа по воздуху 1,17. Определить молекулярную массу газа.
9. Вычислить относительную плотность по воздуху газов: NH3, CH4, N2.
10. Вычислить относительную плотность по воздуху газов: N2O, NO, F2.

11. Вычислить какой объём (н.у.) займут 3,5 г азота; 640 г кислорода; 110 г углекислого газа; 70 г оксида углерода?
12. Какие объёмы занимают при н.у. следующие количества газов: 1 г водорода; 1 г кислорода и 1 г углекислого газа?
13. Сколько молекул содержится в 1 мл водорода при н.у.?
14. Плотность газа по водороду 17. Какова масса 1 л этого газа при н.у.? Какова его плотность по воздуху?
15. Плотность газа по воздуху 1,52. Какой объём займут при н.у. 5,5 г этого газа?
16. Какой объём займут 2∙10 23 молекул хлора при 27 0 С и 600 мм рт. ст.
17. Масса 87 мл пара при 62 0 С и 758 мм рт. ст. равна 0,24 г. Вычислить молекулярную массу вещества.
18. Вычислить массу 1 м 3 воздуха при 17 0 С и 624 мм рт. ст.
19. Вычислить объём, который займёт при 17 0 С и 1 атм. 1кг воздуха.
20. Из опыта найдено, что газ, собранный над водой, при 25 0 С имеет объём 600 мл при атмосферном давлении 97,325 кПа. Вычислить, чему равен объём сухого газа при нормальных условиях.
21. В стальном баллоне ёмкостью 20 л находится кислород под давлением в 12 кПа при температуре 17 0 С. Вычислите массу кислорода в баллоне.
22. Вычислите молекулярную массу газа тремя различным способами, если известно, что массы 1 л воздуха и водорода при н.у., соответственно равны 1,29 и 0,09 г, а масса 1 л газообразного вещества при тех же условиях равна: а) 3,57 г; б) 0,76 г; в) 3,17 г; г)2,058 г; д) 4,82 г; е) 1,965 г; ж) 1,25 г; з) 2,86 г.
Источник