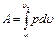Способы изменения состояния газа

Energy
education

сайт для тех, кто хочет изучать энергетику

Термодинамика и тепломассообмен

Идеальный газ

Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

4. Процессы изменения состояния идеальных газов

К основным термодинамическим процессам относят следующие четыре процесса:

• изохорный – при постоянном объеме ($v = const$);
• изобарный – при постоянном давлении ($р = const$);
• изотермический – при постоянной температуре ($Т = const$);
• адиабатный – без теплообмена с внешней средой ($\mathrmq = 0$).

В реальных условиях указанные ограничения практически не выполняются. В связи с этим в технической термодинамике существует понятие политропного процесса как общего случая термодинамического процесса. Предполагается, что политропный процесс обратим и теплоемкость рабочего тела (идеального газа) $с_n$ в ходе данного процесса не изменяется ($c_n=const$). Уравнение политропного процесса имеет вид:

где $n=\frac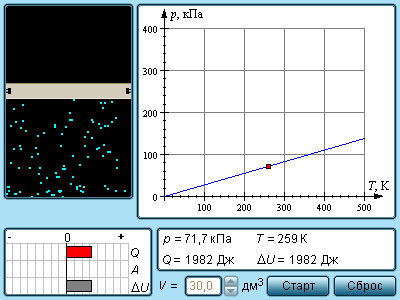$ – постоянная величина, называемая показателем политропы. Политропных процессов существует бесчисленное множество, т.к. $–∞ Изохорный процесс.

Изобарный процесс – термодинамический процесс, происходящий в системе при постоянном давлении. Параметры состояния идеального газа на изобаре связаны соотношением:

Отсюда следует, что чем выше температура газа, тем больше его удельный объем (т.е. тем меньше плотность). При этом величина v на изобаре при повышении температуры растет тем быстрее, чем меньше давление.

Работа расширения системы в изобарном процессе определяется следующим образом:

Для идеального газа работа расширения системы в изобарном процессе может быть представлена также в следующем виде:

Количество теплоты, сообщаемой системе при нагреве (или отдаваемой системой при охлаждении) в изобарном процессе, определяется следующим образом:

$$\mathrmq=\mathrmh+\mathrml’=\mathrmh-v \mathrmp=\mathrmh=c_p \mathrmT,$$

Изменение энтропии в изобарном процессе, т.е. разность энтропий, соответствующих состояниям 1 и 2, определяется из соотношения:

Изотермический процесс – процесс изменения состояния термодинамической системы при постоянной температуре.

Для идеального газа давления и объемы в любых точках на изотерме связаны уравнением Бойля—Мариотта, т.е. зависимость объема от давления на изотерме для идеального газа имеет характер гиперболы:

Работа расширения системы в изотермическом процессе между точками изотермы 1 и 2 определяется с помощью общего соотношения:

Количество теплоты , подводимой к системе (или отдаваемой системой) в изотермическом процессе, определяется из известного соотношения:

Количество работы, совершаемой идеальным газом в изотермическом процессе, равно количеству теплоты, подведенной к этому газу:

Изменение энтропии в изотермическом процессе, т.е. разность энтропий, соответствующих состояниям 1 и 2, вычисляется следующим способом:

Адиабатный процесс – такой термодинамический процесс, в котором к системе не подводится и от системы не отводится теплота. Термодинамическую систему, в которой протекает адиабатный процесс, можно представить себе в виде некоторого объема, ограниченного оболочкой, снабженной идеальной теплоизоляцией, абсолютно не пропускающей теплоту. В реальных условиях процесс является адиабатным в тех случаях, когда система снабжена хорошей теплоизоляцией или когда процесс расширения (сжатия) газа происходит настолько быстро, что не успевает произойти скольконибудь заметный теплообмен газа с окружающей средой.

Поскольку для обратимого процесса $\mathrmq=T \mathrms$, получаем, что в обратимом адиабатном процессе $\mathrms=0$, т.е. энтропия системы сохраняется постоянной. Иными словами, обратимый адиабатный процесс является в то же время изоэнтропным процессом.

Для любого состояния системы в изоэнтропном процессе справедливо соотношение Пуассона:

Если показатель изоэнтропы $k$ изменяется с изменением состояния системы и известен характер зависимости $k$ на изоэнтропе, то для расчета величины $p_2$ по известным $p_1$, $v_1$ и $v_2$ следует вычислить интеграл, стоящий в правой части по известным значениям $k$.

Для идеального газа показатель изоэнтропы $k$ можно определить:

Так как для идеального газа $c_p=c_v+µR$, тогда:

Как известно, теплоемкости идеального газа слабо изменяются с температурой, поэтому и величину $k$ с высокой степенью точности можно считать практически не зависящей от температуры. Известно, что мольная изохорная теплоемкость $μс_v$ идеального газа равна примерно $13$ кДж/(кмоль·К) для одноатомного идеального газа, $21$ кДж/(кмоль·К) для двухатомного и $29$ кДж/(кмоль·К) для трех- и многоатомного газа. Поскольку $µR≈8.3$ кДж/(кмоль·К), то получаем следующие примерные значения показателя изоэнтропы $k$ идеального газа: одноатомный $k=1.67$, двухатомный $k=1.40$, трех- и многоатомный $k=1.29$. Для воздуха показатель изоэнтропы в идеально-газовом состоянии равен примерно $1.40$.

Для изоэнтропного процесса в идеальном газе можно получить соотношения, связывающие между собой значения $p$, $Т$ и $v$:

Работа расширения системы в изоэнтропном процессе определяется следующим образом:

Таким образом, в адиабатном процессе работа расширения системы совершается за счет убыли внутренней энергии системы. Это и понятно – ведь в адиабатном процессе к системе нет притока теплоты извне и единственный источник энергии для совершения работы – внутренняя энергия самой системы.

В случае идеального газа уравнения для расчета работы расширения могут быть представлены также в иной форме:

Следует подчеркнуть, что уравнение выше пригодно для расчета в том случае, если в интервале параметров между точками 1 и 2 показатель изоэнтропы $k$ сохраняется постоянным.

Политропные процессы. Политропными называют термодинамические процессы, удовлетворяющие уравнению:

при произвольном, постоянном для данного процесса значении $n$.

Понятие о политропных процессах было введено в термодинамике по аналогии с понятием об адиабатных процессах. Уравнение политропного процесса по внешнему виду сходно с уравнением адиабаты, однако существенная разница между этими уравнениями состоит в том, что если показатель изоэнтропы (адиабаты) $k$ является в общем случае величиной переменной, то уже само понятие политропного процесса основано на предположении о том, что показатель политропы n является постоянной величиной. В политропном процессе к системе может подводиться (или отводиться от нее) теплота.

Понятие о политропных процессах широко используется главным образом при изучении процессов сжатия и расширения в газовых двигателях, зачастую политропные процессы оказываются удобными для аппроксимации действительных газовых процессов в двигателях. Реальные процессы сжатия в газовых двигателях и компрессорах часто не являются ни адиабатными, ни изотермическими, а занимают промежуточное положение между этими двумя видами процессов. Поэтому обычно встречаемые на практике значения показателя n политропного процесса лежат в интервале от $1$ до $k$.

Если политропный процесс осуществляется в идеальном газе, то нетрудно получить зависимости между начальными и конечными параметрами процесса:

Работа расширения системы в политропном процессе между точками 1 и 2 определяется с помощью уравнения:

Это уравнение можно преобразовать в вид:

Количество теплоты , подводимой к системе (или отводимой от нее) в политропном процессе можно определить с помощью уравнения первого закона термодинамики:

Тогда теплоемкость идеального газа в политропном процессе:

Изменение энтропии системы в политропном процессе, т.е. разность энтропий, соответствующих точкам 1 и 2 на политропе, определяется из соотношения:

Для того чтобы определить значение показателя политропы для того или иного конкретного газового процесса, надо располагать экспериментальными данными для этого процесса.

Администратор сайта: Колосов Михаил
email:
Copyright © 2011-2021. All rights reserved.

Источник

Процессы изменения состояния идеальных газов

Исследования термодинамических процессов, происходящих под влияни­ем тех или иных причин, проводятся по двум направлениям:

1) устанавливают закономерность изменения состояния газа;

2) выявляют особенности превращения энергии.

При изучении изменения состояния газа: 1 — выводят уравнение про­цесса и устанавливают соотношения между параметрами состояния газа; 2 — определяют количество теплоты, подводимой к газу, изменение его внутренней энергии и внешнюю работу, совершаемую газом.

Часто встречаются такие процессы изменения состояния газов, ко­торые протекают в условиях, ограничивающих характер изменения их состояния, на­пример процессы, происходящие:

1) при постоянном объеме рабочего тела (изохорный);

2) при постоянном давлении рабочего тела (изобарный);

3) при постоянной температуре рабочего тела (изотермический);

4) при отсутствии теплообмена между рабочим телом и внешней средой (адиабатный).

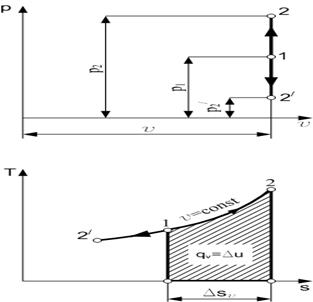
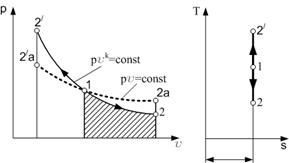
Изохорный процесс

Примером изохорного процесса может быть нагревание или охлажде­ние газа в за­крытом сосуде. Уравнение процесса будет иметь вид v = const. Если точка 1 ха­рактеризует на­чальное состояние газа, то при нагревании ко­нечное состояние газа, в соответствии с законом Шарля, будет характеризо­ваться точкой 2, рас­положенной выше точки 1, а при охлаждении — точкой 2′, распо­ложенной ниже точки 1 (рис. 1.2).

Рис. 1.2. Изохорный процесс измене­ния состояния газа в p-v- и T-s-диаграммах

Если v = const, то dv = 0, и тогда А_v оп­ределяется так:

(1.9)

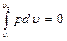
Это значит, что в изохорных процессах теплота, сообщаемая газу, идет только на увеличение его внутренней энергии, а отвод теплоты возможен только за счет уменьшения внутренней энер­гии, то есть

(1.10)

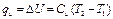
При наличии М, кг, или V, м 3 , газа

(1.11)

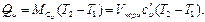
Изменение энтропии в изохорном процессе определяют по равенству

(1.12)

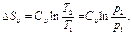
В T-s-диаграмме это уравнение изображается логарифмической кривой, на­правленной выпуклостью к оси абсцисс (рис. 1.2.). В про­цессе 1-2 энтропия воз­растает, следовательно, теплота сообщается газу и он нагревается, а в про­цессе 1-2′ картина противоположная. Площадь под кривой процесса графически изоб­ражает количество теплоты q_v.

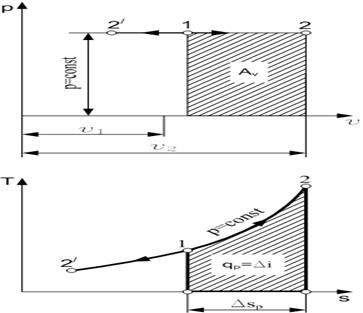
Изобарный процесс

Уравнение изобарного процесса в p-v-коор­динатах р = const, а его график в p-v-диаграмме — это горизонтальная прямая линия (рис. 1.3).

Если точка 1 характеризует начальное состояние газа, процесс изобарного расширения будет представлен линией 1-2, а изобарно­го сжатия — линией 1-2′.

В соответствии с законом Гей-Люссака для процесса 1-2 можно написать

(1.13)

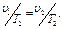
Изменение внутренней энергии идеального газа в изобарных про­цессах определяют по формуле (1.13), а внешнюю работу газа — по об­щей формуле для работы расширения газа

(1.14)

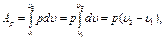
или 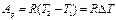(1.15)

Если допустить, что в изобарном процессе 1 кг газа нагревается на 1 гра­дус, то Ар = R.

Отсюда видно, что газовая постоянная R представ­ляет собой ра­боту, производимую в изобарном процессе 1 кг газа при его нагревании на 1 градус.

Теплота, сообщаемая газу в изобарном процессе, может быть вы­ражена через теплоемкость c_v уравнением

или (1.16)

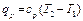
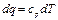
При наличии М, кг, или V, м 3 , газа

(1.17)

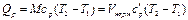
Рис. 1.3. Изобарный процесс измене­ния состояния газа в p-v- и T-s-диаграммах

Изменение энтропии для процесса р = const определя­ется по равенству

(1.18)

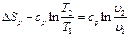
В T-s-диаграмме это урав­нение изображается логариф­мической кривой, направлен­ной выпуклостью к оси абс­цисс (рис. 1.3). В процессе 1-2 энтропия возрастает, т. е. теплота сообщается газу. Количество подведенной теп­лоты графически изображает­ся площадью под кривой процесса.

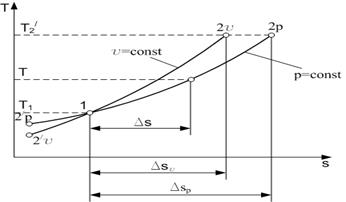
Из сопоставления уравне­ний (1.10) и (1.13) следует, что для одинакового интервала изменения температур (от Т₁ до Т₂) ∆s_p > ∆s_v, так как с_р > с_v.

Это означает, что в T-s-диаграмме изохора всегда круче изобары (рис. 1.4).

В соответствии с уравнением первого закона термодинамики 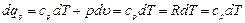(1.19)

Сокращая на AT обе части равенства, получим уравнение Майера

Рис. 1.4. Изохорный и изобарный процессы в T-s-диаграмме.

Если уравнение первого закона термодинамики для процесса р = const написать в виде

(1.21)

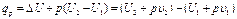
то получим 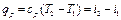(1.22)

и 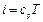(1.23)

Формула (1.23) показывает, что теплота, сообщаемая идеальному газу в изобарном процессе, увеличивает его энтальпию. В диффе­ренциальной форме уравнение для идеального газа принимает вид

(1.24)

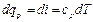
Это уравнение можно получить также исходя из математического определения энтальпии i.

Действительно, поскольку i = U + pv или di = dU + d ( pv ),

то, заменяя pv = RT, получим

(1.25)

(1.26)

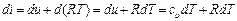
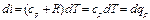
Уравнение (1.24) показывает, что di представляет собой элемен­тарное ко­личе­ство теплоты, сообщаемой телу при нагревании в изо­барном процессе, по­этому ве­личину i назвали энтальпией (от греческого слова enthalpo — нагрева­ние).

В тепло­технических расчетах всег­да необходимо знать изменение энталь­пии, поэтому на­чало ее отсчета не имеет значения. Вообще же его принимают при 0 К или 0 °С.

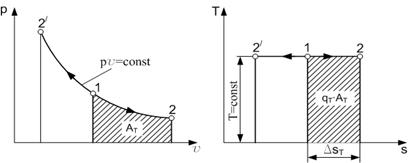
Изотермический процесс

Уравнение этого процесса для идеаль­ного газа выражает закон Бойля-Мариотта (pv = const). График изо­термического процесса в pv-диаграмме, как показывает его уравнение, будет изображаться равнобокой гиперболой, назы­ваемой изотермой. В T-s-диаграмме изотерма является прямой, параллельной оси абсцисс (рис. 1.5).

Процесс расширения 1-2 в T-s-диаграмме изображается прямой, идущей вправо, поскольку расширение газа при постоянной его тем­пературе возможно лишь при подводе теплоты к газу.

Рис. 1.5. Изотермический процесс из­менения состояния газа T-s-диаграммах.

Работа процесса А_т может быть определена из общего выражения для ра­боты газа при его расширении

Заменяя по уравнению состояния газа р = RT/v, находим

(1.27)

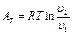
Количество теплоты q_т в T-s-диаграмме изображается площадью прямо­угольника с высотой Т и основанием ∆s_т, т. е. q _т = T∆s_т, где изменение энтропии ∆s_т можно найти из уравнений (1.28) и (1.29) при подстановке Т₁ = Т₂, что дает:

(1.28)

(1.29)

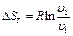
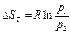
Тогда 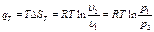(1.30)

Так как изменение внутренней энергии ∆ U в изотермическом про­цессе идеального газа равно нулю, то А_т = q_т .

Адиабатный процесс

Адиабат­ными, как уже отмечалось, назы­ваются процессы изменения сос­тоя­ния, происходящие без подвода и отвода теплоты от газа, т. е. когда dq = 0. При этом и q = 0. Однако не всякий процесс, для которого q = 0, будет адиаба­тичен. Есть процессы, на одной стадии кото­рых теплота подводится, а на дру­гой в том же количестве отводит­ся.

Рис. 1.6. Адиабатный процесс изме­нения состояния газа

в p-v- и T-s-диаграммах.

Таким образом, необходимым и достаточным условием адиабат­ного про­цесса является аналитическое выражение dq = 0, означающее, что в процессе совершенно отсутствует теплообмен. При dq = 0 и Tds = 0, т. е. ds = 0, а это значит, что для обратимых адиабатных процессов s = const. Об­ратимый адиа­батный процесс является в то же время изоэнтропным и в T-s-диа­грамме обра­тимая адиабата будет графически изображаться прямой линией, параллель­ной оси Т. Площадь под кривой процесса будет отсутствовать, т. е. q = 0 (рис. 1.6).

Политропный процесс

Политропными называют процессы, в которых теплоемкость имеет лю­бое, но постоянное на протяжении всего процесса значение. Следо­вательно, в лю­бом по­литропном процессе распределение теплоты между значениями, харак­теризующими изменение внутренней энергии и ра­боту газа, остается не­измен­ным, т. е. отношение dU / dq = c_vdT / cdT = c_v / c = const, где с — постоянная для дан­ного процесса теплоем­кость газа. Уравнение для политропного процес­са изме­нения состоя­ния газа получают из уравнения первого закона тер­мо­ди­намики:

. (1.31)

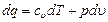
Уравнение политропного или обобщающего процесса изменения состоя­ния газа

. (1.32)

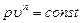
Величина n = (с — с_р)/(с — с _v ) называется показателем политро­пы. В том, что политропный процесс действительно является обобщаю­щим, нетрудно убедиться, представив все рассмотренные ранее процес­сы как частные случаи процесса pv n = const. Например, для изобар­ного процесса уравнение политропы преобразуется в уравнение р = const при n = 0; для изотермы идеального газа n = 1 (pv = const при Т = const); для адиабатного процесса n = k (pv k = const) и, наконец, для изохорного процесса n = ± ∞.

3. Контрольные вопросы по первой теме

1. Что изучают в дисциплине «Теплотехника и энергетические машины»?

2. Что изучают в технической термодинамике?

3. Что такое термодинамическая система?

4. Перечислить основные термодинамические параметры.

5. Взаимосвязь плотности и удельного объема.

6. Назвать единицы измерения температуры.

7. Формула, показывающая взаимосвязь температуры в градусах Цельсия и градусах Кельвина.

8. Из чего состоит энергия рабочего тела, как ее вычисляют?

9. Назвать нормальные физические условия.

10. Написать уравнение Менделеева-Клапейрона для произвольной массы m.

11. Понятие об удельной теплоемкости, единицы ее измерения.

12. Как вычислить количество теплоты, подведенной к телу при изменении его температуры?

13. Понятие об идеальном газе и причинах его использования.

14. Что такое парциальное давление газа в смеси?

15. Математическое выражение закона Дальтона.

16. Какие процессы называют равновесными?

17. Какие процессы называют обратимыми?

18. Перечислить основные термодинамические процессы изменения состояния газа.

19. Что такое изохорный процесс измене­ния состояния газа, как выглядят графики для него в p-v- и T-s-диаграммах?

20. Что такое изобарный процесс измене­ния состояния газа, как выглядят графики для него в p-v- и T-s-диаграммах?

21. Что такое изотермический процесс измене­ния состояния газа, как выглядят графики для него в p-v- и T-s-диаграммах?

22. Что такое адиабатный процесс измене­ния состояния газа, как выглядят графики для него в p-v- и T-s-диаграммах?

23. Что такое политропный процесс измене­ния состояния газа, какая формула его описывает?

24. Что такое энтальпия?

25. Написать уравнение Майера. Что оно показывает?

26. Физический смысл универсальной газовой постоянной R .

Источник