Способы дополнения проекционных чертежей

СПОСОБЫ ДОПОЛНЕНИЯ ПРОЕКЦИОННОГО ЧЕРТЕЖА

Проекции с числовыми (высотными) отметками

Данный способ основан на том, что положение точки в пространстве по отношению к плоскости проекций будет вполне определено, если наряду с проекцией точки будет задана также высота точки, т. е. ее расстояние от плоскости проекций (рис. 1.4). Число, стоящее в скобках рядом с обозначением проекции точки, задает расстояние в единицах приведенного в правом нижнем углу масштаба от данной точки до плоскости проекций. Если число положительное, это значит, что точка находится перед плоскостью проекций, если отрицательное, то точка за плоскостью проекций.

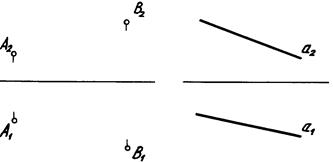
1.2.2. Векторные чертежи (способ Е. С. Федорова)

Академик Е. С. Федоров (1853 – 1919) предложил изображать высоты точек при помощи параллельных отрезков на плоскости проекций, начало которых находится в проекциях соответствующих точек (рис. 1.5). Такие отрезки называются высотными. По направлению отрезка можно судить о том, где находится данная точка, перед плоскостью или за ней. Например, точка А находится перед плоскостью проекций, В – за плоскостью проекций.

Аксонометрические проекции

Аксонометрическое изображение объекта приобретает обратимость за счет отнесения последнего к некоторой прямоугольной системе координат и дальнейшего проецирования этого объекта на плоскость проекций вместе с системой координат.

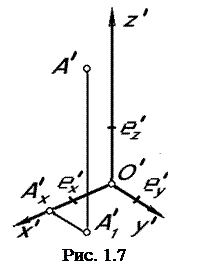
Рассмотрим на примере способ построения аксонометрических проекций (рис. 1.6).

В пространстве имеется объект – точка А. Свяжем жестко эту точку с тремя взаимно перпендикулярными осями декартовой системы координат Oxyz, которую в данном случае называют натуральной системой координат.В качестве единицы измерения, общей для всех трех осей, примем отрезок e, который называется натуральным масштабом.

Для определения положения точки в пространстве строят координатную ломанную линиюOA_xA₁A. Измеряя отрезки этой ломанной натуральным масштабом отрезком e, получаем натуральные координаты точкиA(A_x,A_y,A_z).

Спроецируем теперь точкуА вместе с осями координат Oxyz по направлению S на некоторую плоскость проекций П’, которую называют аксонометрическойплоскостьюпроекций. Проекции геометрических элементов на плоскость П’ называют аксонометрическими:

A’–аксонометрическая проекция точкиА;

O’x’y’z’ –аксонометрическая система координат;

O’A’_xA’₁A’ –аксонометрическая координатная ломаная линия;

A’₁ —вторичная проекция точкиА;

В общем случае проекции e’_x ,e’_y ,e’_z натурального масштаба e различны, т. е. для каждой оси получается свой аксонометрический масштаб.

Для определения точки А на аксонометрической проекции недостаточно иметь только ее аксонометрическую проекциюA’.Нужно также иметь ее вторичную проекцию A’₁, причем прямая A’₁ A’должна быть параллельна аксонометрической оси z’ (рис. 1.7).

Имея точки A’и A’₁, можно провести через точку A’₁ прямую, параллельную y’, в пересечении которой с осью x’ получим точку A’_x, и проекция аксонометрической координатной ломаной O’A’_x A’₁ A’ будет определена.

Если измерить аксонометрические координатные отрезки O’A’_x, O’A’_y, O’A_z натуральным масштабом е, то получим аксонометрические координаты точки А:

,

которые, в общем случае, отличаются от натуральных координат.

Если измерить отрезки аксонометрической координатной ломаной O’A’_xA’₁A’аксонометрическими масштабами e’_x ,e’_y ,e’_z, то получим натуральные координаты точки А:

,

т. к. при параллельном проецировании натуральные координатные отрезки и натуральные масштабы по осям искажаются одинаково по каждой оси.

Таким образом, аксонометрическая проекция, являясь однокартинным изображением объекта, обладает свойством обратимости, т. к. позволяет определить положение объекта (в нашем случае точки А) относительно натуральной системы координат Oxyz.

Комплексный чертеж

Проецирование объекта на две или более плоскости проекций позволяет однозначно определить положение его точек в пространстве. Получаемый при этом чертеж объекта называют комплексным чертежом в ортогональных проекциях или комплексным чертежом.

Принцип построения комплексного чертежа состоит в том, что объект проецируется ортогонально на две взаимно перпендикулярные плоскости проекций. Одна из плоскостей проекций П₁ располагается горизонтально и называется горизонтальной плоскостью проекций (рис. 1.8). Плоскость П₂ располагается вертикально, ее называют фронтальной плоскостью проекций. Плоскости П₁ и П₂ бесконечны и непрозрачны. Линия пересечения плоскостей проекций называется осью проекцийи обозначаетсяx₁₂. Плоскости проекций делят пространство на четыре двухгранных угла – четверти, нумерация которых приведена на рис. 1.8.

При ортогональном проецировании считают, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций.

При построении проекций необходимо помнить, что ортогональной проекцией точки на плоскость проекций является основание перпендикуляра, опущенного из данной точки на эту плоскость проекций.

Спроецируем ортогонально на плоскости проекций П₁ и П₂ какую-нибудь точку А, тогда получим:

А₁ –горизонтальную проекцию точки А на плоскости П₁;

А₂ – фронтальную проекцию точки А на плоскости П₂.

Множество проекций точек пространства на каждой из плоскостей проекций называется полем проекций.

Чтобы получить плоский чертеж, поле проекций на П₁ поворачивается на 90 ° до совмещения с полем проекций на П₂ (рис. 1.9). Убрав искусственные границы плоскостей П₁ и П₂ (эти плоскости безграничны, на рис. 1.9 границы даны для наглядности), получаем комплексный чертеж точки А (рис. 1.10), где:

А₁ А₂ – линия проекционной связи – прямая, перпендикулярная оси проекций x₁₂;

|А₁ А_х| – глубина точкиА – расстояние от нее до фронтальной плоскости проекций П₂;

|А₂ А_х| – высота точкиА – расстояние от нее до горизонтальной плоскости проекций П₁.

Полученный комплексный чертеж обладает свойством обратимости, т. е. по нему можно определить или, как говорят, реконструировать оригинал. Применительно к нашему случаю (рис. 1.10) надо восстановить перпендикуляр к плоскости чертежа в его точке А₂ и от плоскости чертежа отложить глубину |А₁ А_х| искомой точки, тогда конец перпендикуляра определит положение точки А.

Рассмотренный принцип образования комплексного чертежа получил со времен Гаспара Монжа широкое распространение в учебной литературе. Однако в технической практике нет необходимости в определении положения изображаемого оригинала относительно неподвижной системы плоскостей проекций. Поэтому при разработке комплексного чертежа можно отказаться от фиксации плоскостей проекций и получить безосный комплексный чертеж (рис. 1.11.)

Источник

Способы дополнения однокартинного чертежа

Способ с числовыми отметками.Суть способазаключается в том, что недостающая в плоскости проекций пространственная координата отмечается на чертеже числом. Этот способ широко применяется в топографии, при пост-роении профиля дорог, в том числе железнодорожного пути.

Способ академика Федорова. Принципиальное отличие от предыдущего способа состоит в том, что числовые отметки заменяются масштабными отрезками. Способ в основном применяется в кристаллографии.

Способ составления аксонометрических проекции применяют в строительных и машиностроительных чертежах в основном для наглядного изображения предмета.

Способ составления комплексного чертежа наиболее широко применяется при составлении строительных и машиностроительных чер-
тежей.

2. ТОЧКА, ПРЯМАЯ И ПЛОСКОСТЬ НА КОМПЛЕКСНОМ

ЧЕРТЕЖЕ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Прежде чем перейти к изображению геометрических элементов на комп-лексном чертеже, рассмотрим положение некоторой точки А в пространственной системе координат – X, Y, Z (рис. 2.1).

Спроецируем ортогонально точку А на три взаимоперпендикулярные плоскости проекций П₁,П₂,П₃ и получим проекции этой точки: А₁ – горизонтальная; А₂ – фронтальная,
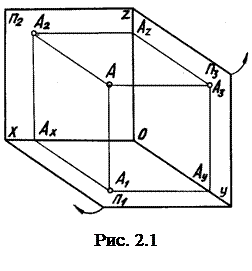
А₃ – профильная. Координаты А_x, A_y, A_z определяют положение этой точки в пространстве. Такое наглядное изображение точки, находящейся в пространстве, дает представление о расположении точки относительно плоскостей проекций П₁, П₂, П₃. Однако в этом случае искажаются действительные размеры в системе координат и, самое главное, затрудняется чтение чертежа при изображении сложных предметов. Французский геометр Г. Монж предложил перейти от такого изображения предмета к комплексному чертежу. Комплексный чертеж – это ортогональное изображение предмета на две или более взаимоперпендикулярные плоскости проекций, совмещенные с плоскостью чертежа. Это совмещение происходит следующим образом: плоскости П₁ и П₃ поворачиваются относительно осей X и Z до положения,
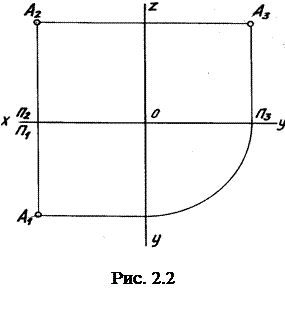
когда они составляют одну плоскость с П₂ (рис. 2.2).

На таком комплексном чертеже точка будет изображаться своими проекциями. Чтобы точка на чертеже была задана, достаточно иметь две ее проекции. Размеры представляются на комплексном чертеже в натуральную величину. Предмет можно изучать спереди, сверху, слева, но при этом необходимо иметь навыки пространственного представления на таком чертеже.

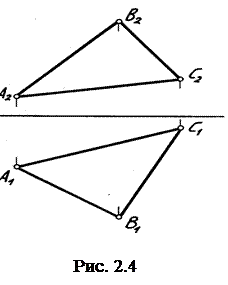
Прямая на комплексном чертеже может быть задана двумя точками или своими проекциями. Минимальное количество проекций прямой на чертеже – две (рис. 2.3).

Плоскость на комплексном чертеже может быть задана тремя точками, точкой и прямой, двумя пересекающимися прямыми, двумя параллельными прямыми, плоской геометрической фигурой (треугольник, окружность и т. д.) и др. Плоскость на комплексном чертеже определяют две ее проекции (рис. 2.4).

3. ПРЯМЫЕ И ПЛОСКОСТИ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Источник

Способы проекций

Рассмотрим некоторые способы дополнения проекционного изо­бражения, позволяющие сделать его «обратимым», то есть однозначно определяющим проецируемый предмет.

Способ проекций с числовыми отметками

Этот способ лежит в основе построения чертежей планов местно­сти и некоторых инженерных сооружений (плотин, дорог, дамб и т.п.).

Способ заключается в том, что положение любой точки в пространстве определяется ее прямоугольной проекцией на некоторую горизонталь­ную плоскость, принятую за плоскость нулевого уровня (рис. 5). Рядом с проекциями точек (а, Ь, с) указывают их отметку. Она указывает рас­стояние от точки до плоскости проекций.

Способ векторных проекций

Академик Е.С. Федоров предложил изображать высоты точек при помощи параллельных отрезков на плоскости проекций. Начало этих от­резков находится в проекциях соответствующих точек (рис. 6). Направ­ление всех высотных отрезков произвольно.

Если точки расположены выше горизонтальной плоскости, высот­ные отрезки, а также числовые отметки считаются положительными, ес­ли ниже — отрицательными. Положительные и отрицательные высотные отрезки в «федоровских проекциях» отличаются противоположным на­правлением. Такие чертежи применяют в геологии, горном деле, топо­графии.

Метод прямоугольных проекций (метод Монжа)

Чертеж в системе прямоугольных проекций образуется при про­ецировании предмета не на одну, а на две или три взаимно перпендику­лярные плоскости проекций. Этот способ является частным случаем па­раллельного проецирования.

Направление проецирования I перпендику­лярно плоскости проекций. Из точки опускается перпендикуляр на плос­кость проекций. Основание перпендикуляра является прямоугольной (ортогональной) проекцией точки.

Осуществлять проецирование на две взаимно перпендикулярные плоскости впервые предложил Гаспар Монж.

Такое проецирование обеспечивает обратимость чертежа. Обратимость чертежа — однозначное определение положения точки в пространстве по ее про­екциям.

Одну из плоскостей принято распола­гать горизонтально — ее называют горизон­тальной плоскостью проекций H (от греч. hori­zon — разграничивающий), другую — ей пер­пендикулярно. Такую вертикальную плоскость называют фронтальной плоскостью проекций V (от лат. — vertical is — отвесный). Эти плоско­сти проекций пересекаются по линии, которая называется осью проекций х (рис. 7).

Чтобы получить проекции точки на плоскости, опускаем из точки А в простран­стве перпендикуляры (проецирующие лучи) до встречи с плоскостями Н и V.

Для полного выявления наружных и внутренних форм деталей и их соединений и для ряда других задач бывает необходимо три и более изображения. Введем в систему плоскостей Н и V третью плоскость. Распо­лагаем ее перпендикулярно этим плоскостям.

Новая плоскость называется профильной плоскостью проекций и обозначается буквой W. Она пересекает плоскости H и V по осям y и z. Точку пересечения всех осей называют началом координат и обозначают буквой O (от ла­тинского слова «origo» — начало). Оси x, у, z взаимно перпендикулярны.

Три взаимно-перпендикулярные плоскости делят пространство на восемь частей, восемь октантов (рис. 8) (от лат. octo — восемь).

В нашей стране принята европейская система расположения про­екций. Ось x направлена от начала координат влево, у — вперед (к нам), z — вверх (x — ось широт, у — ось глубин, z — ось высот). Обратные направ­ления координатных осей считаются отрицательными.

Источник