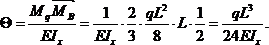Определение перемещений с помощью способа Верещагина

В 1925 г. А. Н. Верещагин предложил простой графоаналитический прием вычисления интеграла Мора в случаях, когда эпюра M z 1 (или M z ) ограничена прямыми линиями. По существу это прием графоаналитического вычисления определенного интеграла от произведения двух функций f ( x ) и φ ( x ), из которых одна, например φ ( x ), линейная, т. е. имеет вид

.

Рассмотрим участок балки, в пределах которого эпюра изгибающих моментов от единичной нагрузки ограничена одной прямой линией M z 1 = kx + b , а изгибающий момент от заданной нагрузки изменяется по некоторому произвольному закону M z . Тогда в пределах этого участка

.

Второй интеграл представляет собой площадь ω эпюры M z на рассматриваемом участке, а первый — статический момент этой площади относительно оси y и поэтому равен произведению площади ω на координату ее центра тяжести x c . Таким образом,

.

Здесь kx c + b — ордината y c эпюры M z 1 под центром тяжести площади ω . Следовательно,

.

Произведение ω y c будет положительным, когда ω и y c расположены по одну сторону от оси эпюры, и отрицательным, если они находятся по разные стороны от этой оси.

Итак, по способу Верещагина операция интегрирования заменяется перемножением площади ω одной эпюры на ординату y c второй (обязательно линейной) эпюры, взятой под центром тяжести площади ω .

Важно всегда помнить, что такое «перемножением» эпюр возможно лишь на участке, ограниченном одной прямой той эпюры, с которой берется ордината y c . Поэтому при вычислении перемещений сечений балок способом Верещагина интеграл Мора по всей длине балки надо заменить суммой интегралов по участкам, в пределах которых эпюра моментов от единичной нагрузки не имеет изломов. Тогда

.

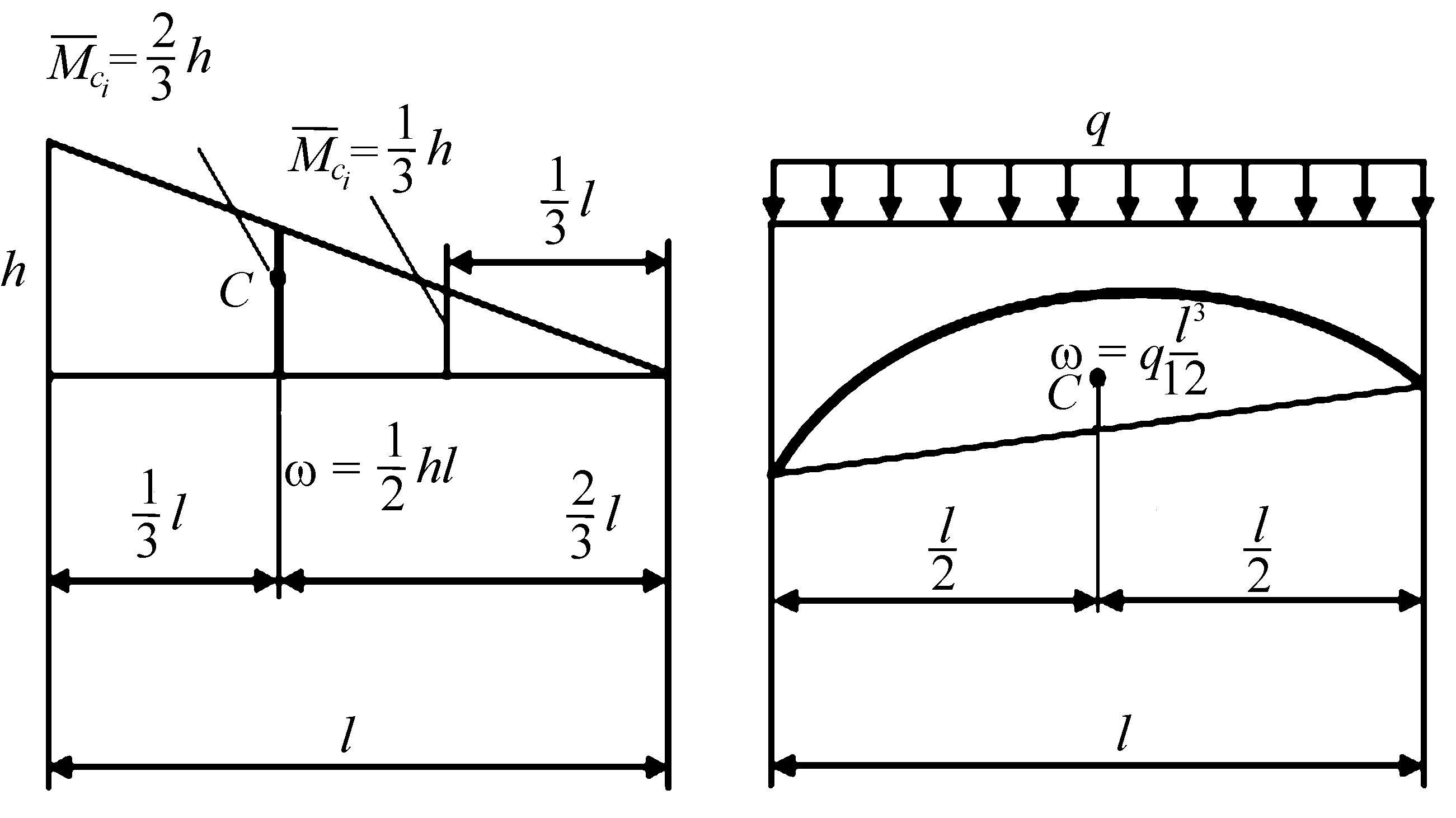
Для успешного применения способа Верещагина необходимо иметь формулы, по которым могут быть вычислены площади ω и координаты x c их центров тяжести. Приведенные в табл. 8.1 данные отвечают только наиболее простым случаям нагружения балки. Однако более сложные эпюры изгибающих моментов допустимо разбивать на простейшие фигуры, площади ω i , и координаты y ci которых известны, а затем находить произведение ω y c для такой сложной эпюры суммированием произведений площадей ω i ее частей на соответствующие им координаты y ci . Объясняется это тем, что разложение множимой эпюры на части равносильно представлению функции M z ( x ) в интеграле (8.46) в виде суммы интегралов. В некоторых случаях упрощает расчеты построение расслоенных эпюр, т. е. от каждой из внешних сил и пар в отдельности.

Если обе эпюры M z и M z 1 линейные, конечный результат их перемножения не зависит от того, умножается ли площадь первой эпюры на ординату второй или, наоборот, площадь второй на ординату первой.

Для практического вычисления перемещений по способу Верещагина надо:

1) построить эпюру изгибающих моментов от заданной нагрузки (основная эпюра);

2) снять с балки заданную нагрузку (но сохранить опоры) и приложить в сечение, перемещение которого ищется, в направлении этого перемещения единичную силу, когда ищется прогиб, или единичную пару, если искомым является угол поворота;

3) построить эпюру изгибающих моментов от единичной нагрузи (единичная эпюра);

4) разбить эпюры от заданных нагрузок на отдельные площади ω i и вычислить ординаты y Ci единичной эпюры под центрами тяжести этих площадей;

5) составить произведение ω i y Ci и просуммировать их.

Источник

7.4. Определение перемещений способом Верещагина

Для конструкций, состоящих из прямолинейных стержней с постоянным поперечным участком на i—м участке, интегралы Мора удобно вычислять по формуле Верещагина:

. (7.14)

Рассматриваемый подход представляет собою графоаналитический способ. В формуле (7.14) – площадь эпюры грузового силового фактора;– значение ординаты единичного силового фактора под центром тяжести площади;– число площадей. Перемещения по способу Верещагина определяют следующим образом.

1. Строят эпюру изгибающих моментов для заданной системы от внешней нагрузки.

2. Составляют схему единичного загружения и строят эпюру изгибающих моментов от единичной нагрузки .

3. Разбивают эпюры и наn одинаковых участков так, чтобы выполнялись следующие условия:

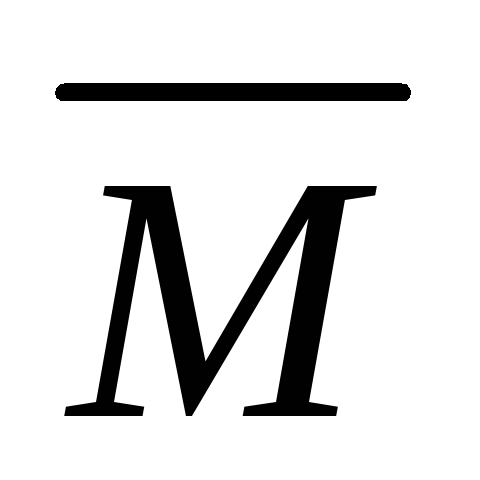
a) под каждым участком эпюры лежал линейный (без изломов и скачков) участок эпюры ;

б) можно было применить известные формулы для вычисления площадей _i участков эпюры и положение центров тяжести этих площадей;

в) изгибная жесткость EJ_х на каждом участке была постоянной.

4. Вычисляют площади _i и ординаты эпюры, расположенных под центрами тяжести площадей_i.

5. Применяют формулу Верещагина, суммируя произведения . Эту операцию называют перемножением эпюр и . Действительное направление искомого перемещения определяется так же, как в методе Мора.

Для того чтобы пользоваться формулой Верещагина, надо знать площадь  и положение центра тяжести для характерных фигур. На рис. 7.5 приводятся необходимые справочные данные.

7.5. Примеры определения перемещений методом Мора и способом Верещагина Пример

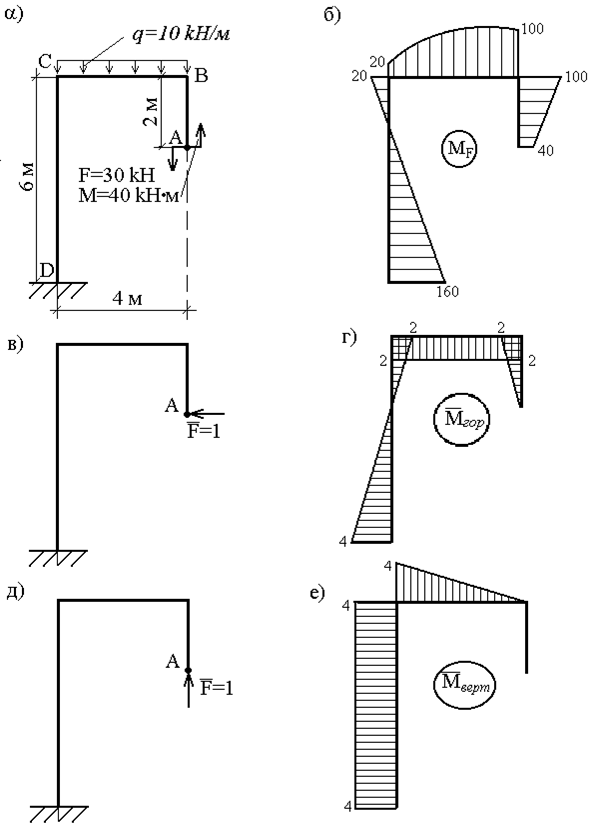
Для заданной стальной балки (рис.7.6, а) подобрать стандартный двутавр из условия прочности. Определить прогиб и угол поворота сечения С, [] = 160 МПа, Е = 210 5 МПа.

Решение

1. Составить уравнения поперечных сил Q_y и изгибающих моментов М_F от внешней нагрузки и построить их эпюры.

Для консольных балок эпюры Q и М можно строить без определения реакций в заделке, если анализ на участках проводить со стороны свободного конца балки в направлении защемления. Выделим балки и участки балки (см. рис. 7.6, а), запишем выражения внутренних усилий и найдем их значения на границах участков.

2. Подобрать двутавровое сечение из условия прочности по _max.

Определяем требуемый момент сопротивления изгибу:

.

Подбираем по ГОСТ 8239–72 двутавр № 27а, у которого W_х = 407,0 см 3 , момент инерции J_х = 5500 см 4 .

3. Определить прогиб сечения С методом Мора.

Составляем схему единичного нагружения, прикладывая к заданной балке безразмерную силу, равную единице в точке С (рис.7.6, г). Разбиваем схему единичного нагружения на такие же участки, что и на схеме грузового нагружения (см. рис. 7.6, а). Записываем для каждого участка выражения изгибающих моментов от единичной нагрузки .

Записываем интегралы Мора на каждом участке и, суммируя результаты, вычисляем прогиб сечения С.

Источник

Правило (способ, метод) Верещагина

Недостатком метода Мора является необходимость получать значения внутренних силовых факторов, входящих в подинтегральные выражения формул (2.18) и (2.19), в общем виде, как функций от z, что становится достаточно трудоемким уже при двух – трех участках разбиения в балках и особенно – в рамах.

Оказывается, что от этого недостатка можно уйти, если непосредственное интегрирование в формулах Мора заменить так называемым перемножением эпюр. Такая замена возможна в тех случаях, когда хотя бы одна из перемножаемых эпюр является прямолинейной. Этому условию соответствуют все системы, состоящие из прямолинейных стержней. Действительно, в таких системах эпюра, построенная от обобщенной единичной силы, всегда будет прямолинейной.

Способ вычисления интеграла Мора путем замены непосредственного интегрирования перемножением соответствующих эпюр называется способом (или правилом) Верещагина и заключается в следующем: чтобы перемножить две эпюры, из которых хотя бы одна является прямолинейной, нужно площадь одной эпюры (если есть криволинейная эпюра, то обязательно ее площадь) умножить на ординату другой эпюры, расположенную под центром тяжести первой.

Докажем справедливость этого правила. Рассмотрим две эпюры (рис.28). Пусть одна из них (Mn) является грузовой и имеет криволинейное очертание, а вторая 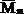соответствует единичной нагрузке и является линейной.

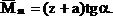
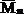
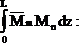
Из рис.28 следует, что Подставим значения в выражение

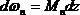
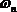
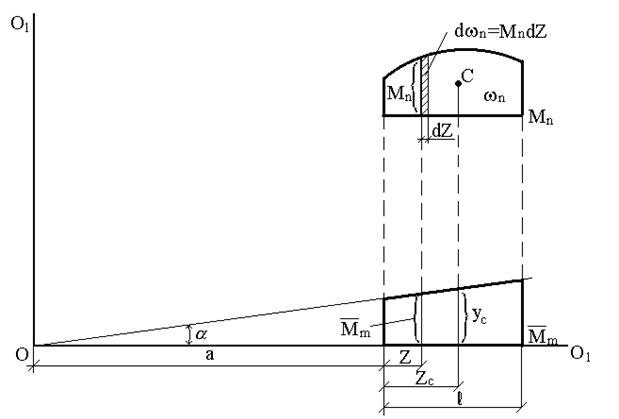
где — дифференциал площади эпюры Mn.

Рис. 28

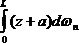
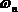
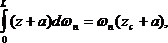
Интеграл представляет собой статический момент площади относительно оси О – О1, при этом:

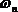
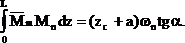
где zc – абсцисса центра тяжести площади , тогда:

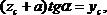
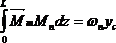
Учитывая, что получим:
(2.20)
Выражение (2.20) определяет результат перемножения двух эпюр, а не перемещения. Чтобы получить перемещение, этот результат нужно разделить на жесткость, соответствующую внутренним силовым факторам, стоящим под знаком интеграла.

Основные варианты перемножения эпюр

Очевидно, что разнообразие приложенных нагрузок и геометрических схем конструкций приводит к различным, с точки зрения геометрии, перемножаемым эпюрам. Для реализации правила Верещагина нужно знать площади геометрических фигур и координаты их центров тяжести. На рис.29 представлены некоторые основные варианты, возникающие в практических расчетах.

Для перемножения эпюр сложной формы их необходимо разбивать на простейшие. Например, для перемножения двух эпюр, имеющих вид трапеции, нужно одну из них разбить на треугольник и прямоугольник, умножить площадь каждого из них на ординату второй эпюры, расположенную под соответствующим центром тяжести, и результаты сложить. Аналогично поступают и для умножения криволинейной трапеции на любую линейную эпюру.

Если указанные выше действия проделать в общем виде, то получим для таких сложных случаев формулы, удобные для использования в практических расчетах (рис.30). Так, результат перемножения двух трапеций (рис.30,а):

(2.21)

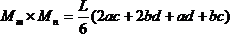
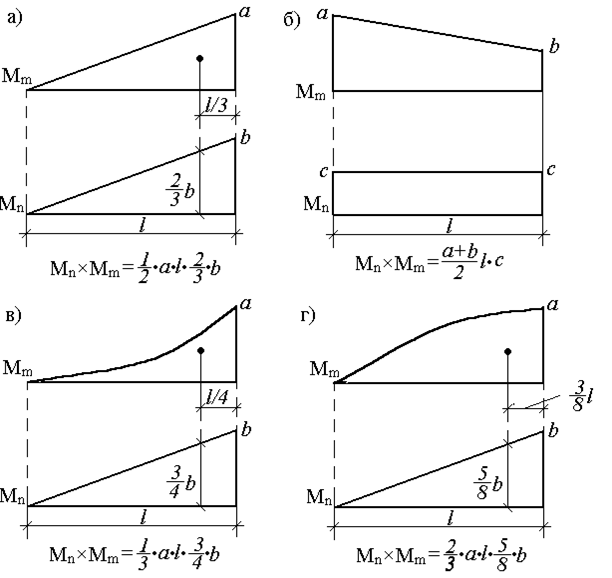
Рис. 29

По формуле (2.21) можно перемножить и эпюры, имеющих вид «перекрученных» трапеций (рис.30,б), но при этом произведение ординат, расположенных по разные стороны от осей эпюр, учитывается со знаком минус.

Если одна из перемножаемых эпюр очерчена по квадратной параболе (что соответствует нагружению равномерно распределенной нагрузкой), то для перемножения со второй (обязательно линейной) эпюрой ее рассматривают как сумму (рис.30,в) или разность (рис.30,г) трапециидальной и параболической эпюр. Результат перемножения в обоих случаях определяется формулой:
(2.22)

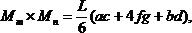
но значение f при этом определяется по-разному (рис. 30, в, г).

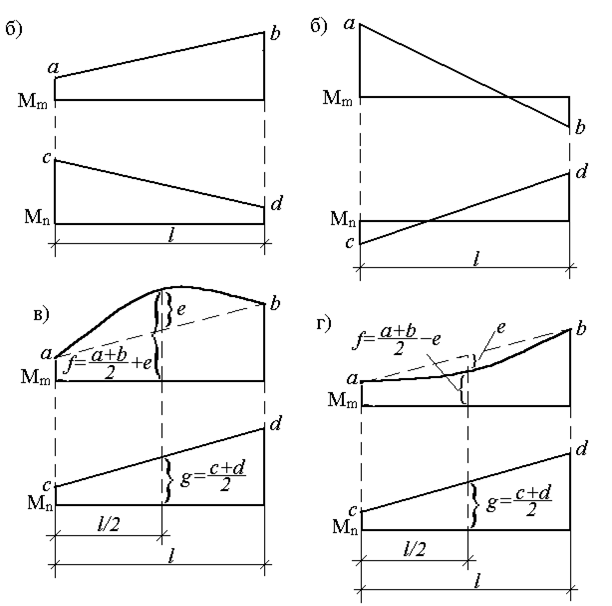
Рис. 30

Возможны случаи, когда ни одна из перемножаемых эпюр не является прямолинейной, но хотя бы одна из них ограничена ломаными прямыми линиями. Для перемножения таких эпюр их предварительно разбивают на участки, в пределах каждого из которых по крайней мере одна эпюра являетя прямолинейной.
Рассмотрим использование правила Верещагина на конкретных примерах.

Пример 15. Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.31,а), способом Верещагина.

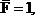
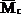
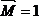
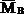
Последовательность расчета способом Верещагина – такая же, как и в методе Мора, поэтому рассмотрим три состояния балки: грузовое – при действии распределенной нагрузки q; ему соответствует эпюра Mq (рис.31,б), и два единичных состояния — при действии силы приложенной в точке С (эпюра , рис.31,в), и момента , приложенного в точке В (эпюра , рис.31,г).

Прогиб балки в середине пролета:

.

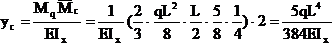
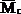
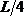
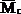
Аналогичный результат был получен ранее методом Мора (см. пример 13). Следует обратить внимание на тот факт, что перемножение эпюр выполнялось для половины балки, а затем, в силу симметрии, результат удваивался. Если же площадь всей эпюры Mq умножить на расположенную под ее центром тяжести ординату эпюры (на рис.31,в), то величина перемещения будет совершенно иной и неправильной так как эпюра ограничена ломаной линией. На недопустимость такого подхода уже указывалось выше.

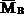
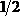
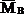
А при вычислении угла поворота сечения в точке В можно площадь эпюры Mq умножить на расположенную под ее центром тяжести ординату эпюры (, рис.31,г), так как эпюра ограничена прямой линией:

Этот результат также совпадает с результатом, полученным ранее методом Мора (см. пример 13).

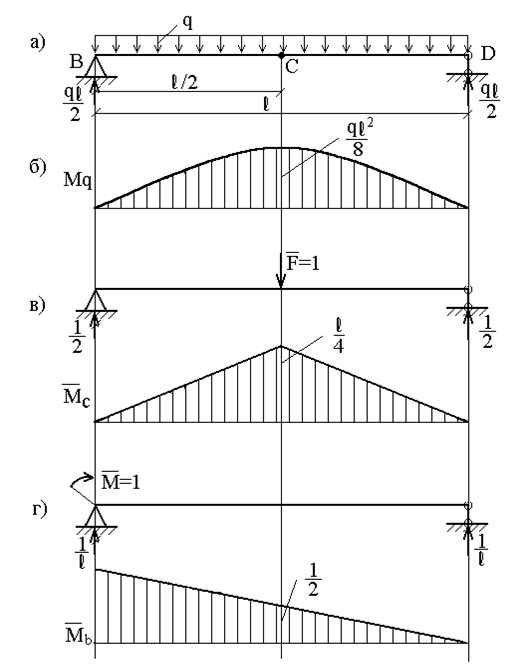
Рис. 31

Пример 16. Определить горизонтальное и вертикальное перемещения точки А в раме (рис.32,а).

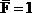
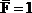
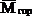
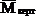
Как и в предыдущем примере, для решения задачи необходимо рассмотреть три состояния рамы: грузовое и два единичных. Эпюра моментов MF, соответствующая первому состоянию, представлена на рис.32,б. Для вычисления горизонтального перемещения прикладываем в точке А по направлению искомого перемещения (т.е. горизонтально) силу , а для вычисления вертикального перемещения силу прикладываем вертикально (рис.32,в,д). Соответствующие эпюры и показаны на рис.32,г,е.

Горизонтальное перемещение точки А:

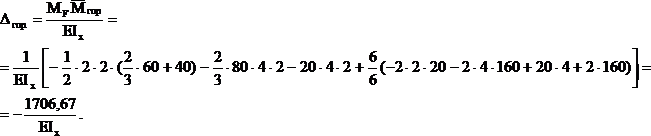
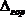
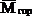
При вычислении на участке АВ трапеция (эпюра MF) разбита на треугольник и прямоугольник, после чего треугольник с эпюры «умножен» на каждую из этих фигур. На участке ВС криволинейная трапеция разделена на криволинейный треугольник и прямоугольник, а для перемножения эпюр на участке СД использована формула (2.21).

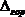
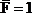
Знак » — «, полученный при вычислении , означает, что точка А перемещается по горизонтали не влево (в этом направлении приложена сила ), а вправо.
Вертикальное перемещение точки А:

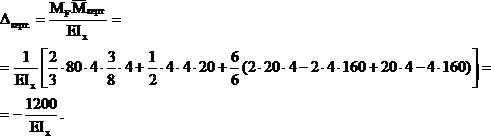
Здесь знак » — » означает, что точка А перемещается вниз, а не вверх.

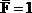
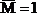
Отметим, что единичные эпюры моментов, построенные от силы , имеют размерность длины, а единичные эпюры моментов построенные от момента , являются безразмерными.

Пример 17. Определить вертикальное перемещение точки А плоско-пространственной системы (рис.33,а).

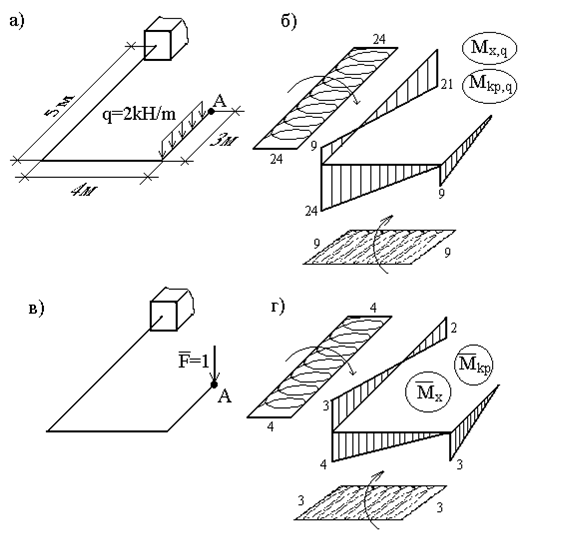
Рис.23

Как известно (см. гл.1), в поперечных сечениях стержней плоско-пространственной системы возникают три внутренних силовых фактора: поперечная сила Qy, изгибающий момент Mx и крутящий момент Mкр. Так как влияние поперечной силы на величину перемещения незначительно (см. пример 14, рис.27), то при вычислении перемещения методом Мора и Верещагина из шести слагаемых остаются только два.

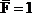
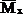
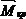
Для решения задачи построим эпюры изгибающих моментов Mx,q и крутящих моментов Мкр,q от внешней нагрузки (рис.33,б), а затем в точке А приложим силу по направлению искомого перемещения, т.е. вертикального (рис.33,в), и построим единичные эпюры изгибающих моментов и крутящих моментов (рис.33,г). Стрелками на эпюрах крутящих моментов показаны направления закручивания соответствующих участков плоско-пространственной системы.

Вертикальное перемещение точки А:

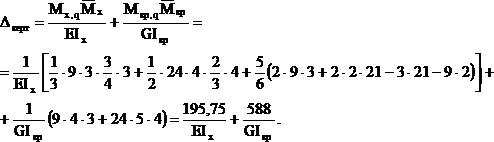
При перемножении эпюр крутящих моментов произведение берется со знаком «+», если стрелки, указывающие направление кручения, сонаправленны, и со знаком » — » – в противном случае.

Источник