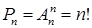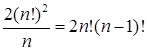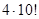Сколькими способами можно обить 6 стульев если имеется 4 вида ткани

Сколькими способами можно обить 6 стульев, если имеется 4 вида ткани?

Математика | 10 — 11 классы

Сколькими способами можно обить 6 стульев, если имеется 4 вида ткани.

Считать, что все стулья одинаковые.

Если стулья одинаковые, то ОДНИМ.

В трех одинаковых рядах 24 стула?

В трех одинаковых рядах 24 стула.

Сколько стульев в каждом ряду?

Сколько стульев в двух таких рядах?

Составить в виде таблицы.

Имеется 3 различных стула и 5 видов различных накидок на стулья?

Имеется 3 различных стула и 5 видов различных накидок на стулья.

Тогда количество способов, которыми можно покрыть эти стулья, равно.

Имеется 3 различных стула и 5 видов различных накидок на стулья?

Имеется 3 различных стула и 5 видов различных накидок на стулья.

Тогда количество способов, которыми можно покрыть эти стулья, равно ….

Ткань 210см на 210см?

Ткань 210см на 210см.

Стул 40см, запас 10см.

Сколько стульев можно обтянуть?

Имеется ткань двух цветов : голубая и зелёная — и требуется обить диван, кресло и стул?

Имеется ткань двух цветов : голубая и зелёная — и требуется обить диван, кресло и стул.

Сколько существует вариантов обивки этой мебели?

Выпишите все эти варианты.

Сколькими способами можно обить 6 стульев если имеется 6 вида ткани и все стулья должны быть разного цвета?

Сколькими способами можно обить 6 стульев если имеется 6 вида ткани и все стулья должны быть разного цвета.

3 одинаковых средах 24 стула Сколько стульев в каждом ряду Сколько стульев 2 таких средах?

3 одинаковых средах 24 стула Сколько стульев в каждом ряду Сколько стульев 2 таких средах.

Добавить данные и решить задачу Купили по одинаковой цене А стульев для библиотеки и В стульев для столовой?

Добавить данные и решить задачу Купили по одинаковой цене А стульев для библиотеки и В стульев для столовой.

За все стулья заплатили С рублей.

Сколько стоили стулья для столовой и сколько для библиотеки?

В трех одинаковых рядах 24 стула?

В трех одинаковых рядах 24 стула.

Сколько стульев в каждом ряду?

Сколько стульев в двух таких рядах?

3 одинаковых стула стоят 630 р?

3 одинаковых стула стоят 630 р.

Сколько стоит один стул.

На этой странице сайта вы найдете ответы на вопрос Сколькими способами можно обить 6 стульев, если имеется 4 вида ткани?, относящийся к категории Математика. Сложность вопроса соответствует базовым знаниям учеников 10 — 11 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

3 — е задание. Ответ 24 см, 32 см, 52см.

1)выражение : 82 + 18 ; 7 + 29 значения выражения : 100 ; 36 2)выражение : 35 — 12 ; 90 — 15 значение выражения : 23 ; 75 3)выражение : 56 : 7 ; 63 : 9 значение выражения : 8 ; 7 4) выражение : 9 * 1 ; 7 * 3 значение выражения : 9 ; 21.

1) 20 + 14 = 34 кг — во втором ящике 2) 20 + 34 = 54 кг — в двух ящиках вместе 3) 54 : 6 = 9 кг яблок — в одном ящике.

Вот, на фотографии все видно.

5 насосов понадобится на 21 акулу.

1) 2136 + 1000 = 3136 3136 / 16 = 196 2) 15 * 5 = 75 55350 / 75 = 738.

(1, 05 + ( — 1 1 / 20)) + 1 : 1 1 / 29 = (1, 05 — 1, 05) + 1 : 30 / 29 = 0 + 29 / 30 = 29 / 30 ответ : 29 / 30.

Изначально в 1 ящике было 5x мандаринов, а во втором x мандаринов, когда из 1 ящика взяли 25 кг, а во второй положили 15кг, то в 1 ящике стало 5x — 25 мандаринов , а во втором x + 15 мандаринов, т. К. в обоих ящиках стало поровну, то получаем следую..

Площадь треугольника по формуле Герона : a = 36 см, b = 25 см, c = 29 см р — полупериметр треугольника p = 45 SΔ = 360 см² формула площади треугольника, если известна сторона и высота проведенная к этой стороне : 1. см 2. см 3. см.

Источник

07. Перестановки

Рассмотрим частный случай, когда k=n. Соответствующее этому случаю размещение называется перестановкой.

Перестановками из n элементов называются такие комбинации, каждая из которых содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Поясним это на следующем примере. Из этих трёх элементов: a, b и c. можно составить шесть перестановок: abc, acb, bac, bca, cab, cba. Все приведённые перестановки отличаются друг от друга только порядком их расположения.

Число перестановок n различных элементов обозначают символом Pn и равно

Пример 5.1. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?

Решение. Будем считать выделенные книги за одну книгу. Тогда уже для шести книг существует P6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой P4=4!=24 способами. По принципу умножения имеем

P6P4 = 720×24 = 17280.

Пример 5.2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в изображении числа встречается один раз?

Решение. Рассматриваемое число может быть представлено как некоторая перестановка из цифр 0, 1, 2, 3, в которой первая цифра отлична от нуля. Так как число перестановок из четырех цифр равно P4=4! и из них 3! перестановок начинаются с нуля, то искомое количество равно

4! – 3! = 3×3! = 3×1×2×3 = 18.

Пример 5.3. Сколькими способами можно посадить за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом?

Решение. Естественно предположить, что как мужчины, так и женщины различимы. Предположим также, что места за столом также различимы. Пронумеруем их. Если женщины займут чётные места n! способами, то мужчины будут занимать нечётные места тоже n! способами и наоборот. По правилу умножения получаем .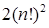

Если места за столом неразличимы, то стол можно поворачивать на одно место, то при этом расположение сидящих не изменится (такая ситуация имеет место, например, на карусели). Поскольку имеется n способов расположения стола относительно сидящих, то предыдущий результат нужно разделить на n.

Вопрос. Сколькими способами можно посадить за круглый стол n супружеских пар, если супруги должны сидеть рядом?

5.1. Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 различных цветов и все стулья должны быть разного цвета.

Ответ: .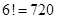

5.2. Дачник выделил на своём участке семь грядок для выращивания овощей, т. к. хочет иметь свои помидоры, огурцы, перец, лук, чеснок, салат и кабачки. Каждый вид должен иметь отдельную грядку. Сколькими способами он может расположить грядки для посадки?

Ответ: .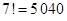

5.3. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?

Ответ: .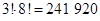

5.4. В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?

Ответ:

5.5. Сколькими способами можно упорядочить множество <1,2,3,…,2n>так, чтобы каждое чётное число стояло на чётном месте?

Ответ: .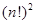

5.6. Четыре мальчика и четыре девочки рассаживаются в ряд на восемь подряд расположенных мест, причем мальчики садятся на четные места, а девочки – на нечетные. Сколькими способами они могут это сделать?

Ответ: .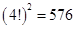

5.7. Сколькими способами можно посадить за круглый стол трех мужчин и трех женщин так, чтобы никакие два лица одного пола не сидели рядом?

Ответ: .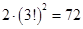

5.8. На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите эту же задачу, если Б должен выступить сразу после А.

Источник

Сколькими способами можно осуществить обивку стульев?

Имеется пять различных стульев и семь рулонов обивочной ткани различных цветов. Сколькими способами можно осуществить обивку стульев?

Добавлено через 38 минут
помогите пожалуйста очень срочно нужно.

Сколькими способами можно разместить 8 человек за столом, у которого стоит 8 стульев?
Сколькома способами можно разместить 8 человек за столом, у которого стоит 8 стульев?

Сколькими способами можно распределить
В распоряжении ГУВД поступило 28 новых одинаковых машин, которые нужно распределить между 4.

сколькими способами можно поставить
Энциклопедия состоит из девяти томов — с первого по девятый.Сколькими способами её можно поставить.

Сколькими способами можно выбрать.?
Сколькими способами можно выбрать 4 набора по 5 карт из колоды, содержащей 52 карты?

Добавлено через 4 минуты
Если цвета могут повторяться, тогда 7^5.

Сколькими способами можно разместить
Сколькими способами можно разместить _ <1>красных, _ <2>желтых и _ <3>зеленых слоев по m.

Сколькими способами можно разменять
Сколькими способами можно разменять 100руб в 5,10,20 и 50 руб? решить рекурсией..помогите.

Сколькими способами можно расселить 15 студентов?
сколькими способами можно расселить 15 студентов в 5 комнат по 3 человека?

Сколькими способами можно собрать число 40 из 10 25 15
Сколькими способами можно собрать число 40 имея три числа 10 25 15 x = 10 y = 25 z = 15 Я.

Источник

07. Перестановки

Рассмотрим частный случай, когда k=n. Соответствующее этому случаю размещение называется перестановкой.

Перестановками из n элементов называются такие комбинации, каждая из которых содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Поясним это на следующем примере. Из этих трёх элементов: a, b и c. можно составить шесть перестановок: abc, acb, bac, bca, cab, cba. Все приведённые перестановки отличаются друг от друга только порядком их расположения.

Число перестановок n различных элементов обозначают символом Pn и равно

Пример 5.1. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?

Решение. Будем считать выделенные книги за одну книгу. Тогда уже для шести книг существует P6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой P4=4!=24 способами. По принципу умножения имеем

P6P4 = 720×24 = 17280.

Пример 5.2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в изображении числа встречается один раз?

Решение. Рассматриваемое число может быть представлено как некоторая перестановка из цифр 0, 1, 2, 3, в которой первая цифра отлична от нуля. Так как число перестановок из четырех цифр равно P4=4! и из них 3! перестановок начинаются с нуля, то искомое количество равно

4! – 3! = 3×3! = 3×1×2×3 = 18.

Пример 5.3. Сколькими способами можно посадить за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом?

Решение. Естественно предположить, что как мужчины, так и женщины различимы. Предположим также, что места за столом также различимы. Пронумеруем их. Если женщины займут чётные места n! способами, то мужчины будут занимать нечётные места тоже n! способами и наоборот. По правилу умножения получаем .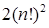

Если места за столом неразличимы, то стол можно поворачивать на одно место, то при этом расположение сидящих не изменится (такая ситуация имеет место, например, на карусели). Поскольку имеется n способов расположения стола относительно сидящих, то предыдущий результат нужно разделить на n.

Вопрос. Сколькими способами можно посадить за круглый стол n супружеских пар, если супруги должны сидеть рядом?

5.1. Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 различных цветов и все стулья должны быть разного цвета.

Ответ: .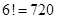

5.2. Дачник выделил на своём участке семь грядок для выращивания овощей, т. к. хочет иметь свои помидоры, огурцы, перец, лук, чеснок, салат и кабачки. Каждый вид должен иметь отдельную грядку. Сколькими способами он может расположить грядки для посадки?

Ответ: .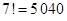

5.3. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?

Ответ: .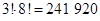

5.4. В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?

Ответ:

5.5. Сколькими способами можно упорядочить множество <1,2,3,…,2n>так, чтобы каждое чётное число стояло на чётном месте?

Ответ: .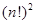

5.6. Четыре мальчика и четыре девочки рассаживаются в ряд на восемь подряд расположенных мест, причем мальчики садятся на четные места, а девочки – на нечетные. Сколькими способами они могут это сделать?

Ответ: .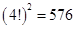

5.7. Сколькими способами можно посадить за круглый стол трех мужчин и трех женщин так, чтобы никакие два лица одного пола не сидели рядом?

Ответ: .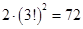

5.8. На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите эту же задачу, если Б должен выступить сразу после А.

Источник