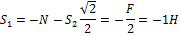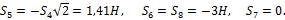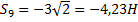Расчет ферм аналитическим способом

Аналитический способ расчета ферм

Аналитический способ расчета ферм

• Аналитические методы расчета ферм для расчета ферм используются два способа: аналитический и графический. Расчет фермы, которая может быть статически определена любым способом, начинается с определения эталонной реакции. В стержне фермы только продольная сжимающая сила или растягивающая сила возникает от внешней нагрузки, приложенной к узлу. Растягивающее продольное (нормальное) усилие стержня фермы считается положительным,

сжимающее-отрицательным. Перед расчетом все внутренние продольные силы положительны. Если в результате расчетов продольная сила в стержне была получена со знаком минус, то этот стержень подвергается сжатию. Внутренняя продольная сила в стержне фермы определяется методом поперечного сечения. В зависимости от записанных уравнений сечений и статических равновесий, выполненных в хозяйстве,

наиболее распространены следующие методы расчета: 1) разрезание узлов;2) сквозное Людмила Фирмаль

разрезание, используются эти методы.; 3423 закрытого раздела). В дополнение к этим методам были разработаны другие специальные методы расчета ферм. Они не установлены в этом курсе. Как отключить узел. Особенностью способа является выполнение такого сечения, при котором одна из ферм вырезается из своего узла. Все остальные фермы отбрасываются, и удар заменяется неизвестной продольной силой, направленной вдоль оси отсеченного стержня. В каждом узле фермы все внешние и внутренние нагрузки

пересекаются в центре узла (и для каждого узла можно составить два независимых уравнения равновесия в виде сумм проекций на две непараллельные оси). Третье уравнение 2L1=0 превращается в тождество. Обычно два уравнения равновесия записываются как 2G=0i2u=0. Мы решаем эти уравнения и находим неизвестные силы в траслодах, сходящихся в данном узле. Поэтому метод режущего узла можно использовать только в том случае, если режущий узел имеет только две неизвестные силы. Порядок расчета фермы по способу

• разрезания узла, количество неизвестных внутренних сил в отключенном узле должно быть меньше двух. Переходите от одного узла к другому и рассчитайте силу всех стержней в ферме. Статически определяемая ферма позволяет разделить узлы треугольника на два стержня, которые всегда рассчитываются путем разрезания узлов. Если в ферме нет узлов, где сходятся два стержня, или если в непрерывном переходе от узла к узлу неизвестной силы их больше двух, то узел будет закрыт. Недостатком данного способа расчета является то, что последующий расчет зависит от предыдущего, и

переход погрешностей при расчете сил в одних стержнях на другие. Этот метод очень полезен при вычислении использования сельскохозяйственных угодий компьютером 343 пример определения продольной силы стержня фермы, как показано на рисунке. 31.9, а. Решение. Найти эталонную реакцию: 2Z=0, tfB=0;= -/?C * 15+ / y5+F-10=0; Rc— (1 7 ,5 -5 + 10-10)/15 = 12,5 кн;РБ-15-Фр1 0-Ф2. 5=0; RB= (17,5-10+ 10-5)/15 = 15 кн. В этой ферме опорные узлы B и C узел B(рис. 31.9, 6): 2U=/?В+^2z1p45° = 0, TVB2= — Rb / sin45° = — 15/0, 707 = — 21,21 кн; SZ=NB2cos45°+Nb2=0, NB i= — jVb2cos45° = — (21,21) — 707 = 15кн. Далее

сходятся в два стержня, поэтому сначала разрежьте один из них, например, Людмила Фирмаль

sin 45°+/?s=0, L / s z=—/?C / sin45° = — 12,5 / 0,707 = — 17,68 кн; SZ= — NC4-NC3cos45°=0, WC4= — WC3cos45° = — (— 17,68)-0,707 = 12,5 кн. Поскольку силы Nc3 и N c4 имеют одинаковое значение, расчеты фермы выполняются правильно. Частный случай в деревне РА Упе я обычно атло век фермы Есть сломанные стержни, и сила равна нулю для данной нагрузки. Такой стержень называется нулем. 1) когда внешняя нагрузка не приложена к узлу, где сходятся только два ядра, сила этих ядер будет равна нулю (рис. 31.10 а). Фактически она получается из состояния равновесия: 2U=L^sin a=0,2 Vi=0; SZ=i C O s a=0,2, M2=0; 2) если три стержня сходятся на узле холостого хода, а два из них

направлены под углом к одному, то силы в стержнях направлены раздельно и направлены друг к другу на фиг. 31.10, 6). Из уравнения sy=N3sin a=0 найдем MZ=0. Из уравнения SZ= — +находим ^i=a^2; 3453) если четыре стержня сходятся на узле холостого хода, то две пары находятся на одной прямой, и сила стержней, направленных на одну прямую, равна друг другу(рис. 31.10 б). Из состояния равновесия 2U=0 находим M3=M4. Из состояния равновесия SZ=0 находим L^=LG2; 4) если нагрузка F приложена к стержневому узлу, два стержня которого находятся на одной линии, а третий-31.10 g). Путь точки крутящего момента. В этом методе сквозная ферменная конструкция разрезается на две части таким образом, что три или более стержней с

неизвестной силой не разрезаются.1 в этом случае оси этих отрезанных стержней не должны пересекаться в одной точке. Часть фермы отбрасывается, ее действие на остальные заменяется внутренней продольной силой, направленной вдоль оси срезаемого стержня. 1 это требование определяется тем фактом, что для плоской системы сил можно построить только три уравнения статического равновесия, Восемьсот сорок шесть Для остальных напишите три уравнения момента для трех точек плоскости, которые не лежат в одной прямой. Если взять любую точку,то при определении трех неизвестных сил нужно решить систему из трех уравнений с трем

я неизвестными. Для упрощения расчета точку, расположенную на пересечении осей трех отрезанных стержней, делают точкой крутящего момента. В этом случае мы получаем три независимых уравнения, каждое из которых содержит только неизвестную силу. Этот метод расчета фермы называется методом точки крутящего момента. Преимущество этого метода перед методом нарезания Сучков заключается в том, что сила любого стержня определяется независимо от силы других стержней. Например. В хозяйстве, как показано на рисунке. 3.11, а, определение силы N2z, / U24 и l / I в стержне 2-5, 2-4 и 1-4. Решение. Находим эталонную реакцию: SZ=0,

JV=0; 2L1B=Ff5+F2. 10+F3. 1 5-Z? c-20=0,/?C j= (6-5 + 16-10 4 — 8 — 15)/20 = 15,5 kN;£MS=RB-20-Ff15-F2-Yu-F3’5 = 0, RB= (6-15+ 16-10+ 8 -5 )/2 0 = 14,5 кн. Проверка: 2U=0; Rb-F-Ft-Fs+R c^M Ji—6—16—8+15,5 = 0. Отрежьте ферму через секцию 1-1 до второй панели. Отбросьте правую часть и оставьте ее слева(рис. 3.11, б). Точкой крутящего момента для определения силы является пересечение стержней 2-4 и 1-4, то есть узел 4. =^23+pb.10-f1. 5=°, N23=(«•10+M) / r23= (» 14 ‘5 *10 + 6 *5)/10 грех 30°= = — 23кн. Точка крутящего момента для определения силы W24 находится на пересечении стержней 1-4 и 2-3.: W T=V24+M = °- = — R R5 / rs l=— 6,5/10 • грех 30°= — 6кн. Точкой крутящего момента для

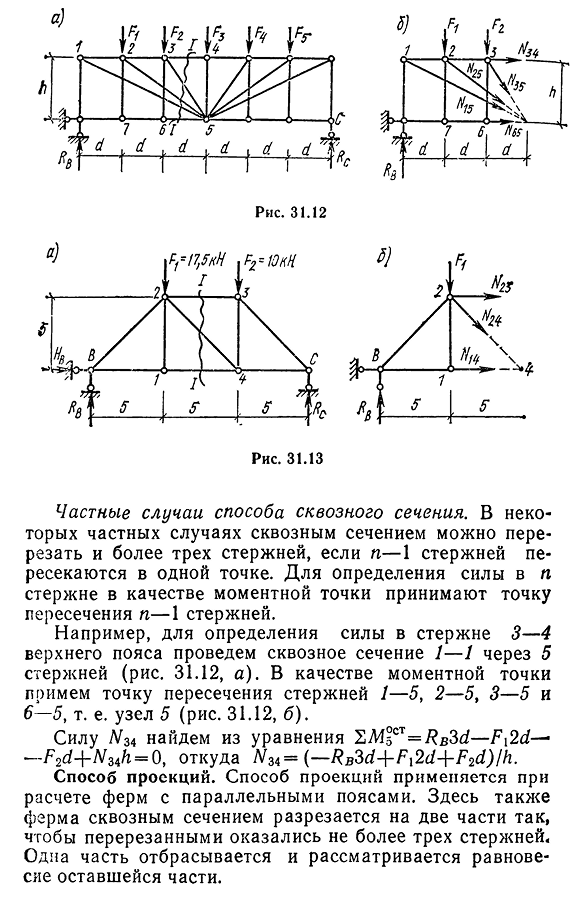
определения силы L / / 4 является точка пересечения стержней 2-3 и 2-4, то есть узел 2:+ ‘ 5= L\4=RB5/Gy=14,5-5/5tg30°=25,13 кн. 347частные примеры методов через разделы. В некоторых особых случаях сквозное сечение может быть разрезано, и если N-1 стержень пересекается в одной точке, то можно разрезать три или более стержней. Возьмите пересечение N-1 стержня, чтобы определить силу в N-стержне в качестве точки крутящего момента. Например, для определения силы тяги 3-4 на верхнем поясе сечения 1-1-5 тяг (рис. 31.12, а). В качестве точки момента точка пересечения стержня является 1-5, 2-5,3-5, 3-5, 6-5, т. е. узел 5(фиг. 31.12, б). Сила Af34 = / где

была найдена формула SM5CT?B3d-Fi2d—F2rf+^34^=0, где W34= (- RB^d+Fl2d+F2d) / ч. Проекция. Проекционный метод используется для расчета ферм с параллельными поясами. Опять же, ферму разрезают на две части поперечного сечения, так что вырезается не более трех стержней. Одна часть отбрасывается, а остаток остальных частей принимается во внимание. В отличие от метода 348 точек крутящего момента, в этом методе третье уравнение момента заменяется уравнением проекции на ось, перпендикулярную поясу фермы. Такая подстановка вызвана тем, что момент точки пересечения осей стержней параллельного Ферменного пояса бесконечен. Остальные методы расчета те же, что и для расчета мгновенных точек.

Если вам потребуется помощь по технической механике вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Расчет ферм. Понятие о ферме. Аналитический расчет плоских ферм.

Расчет ферм. Трение скольжения и качения.

Изучение данных вопросов необходимо в дальнейшем для изучения динамики движении тел с учетом трения скольжения и трения качения, динамики движения центра масс механической системы, кинетических моментов, для решения задач в дисциплине «Сопротивление материалов».

Расчет ферм. Понятие о ферме. Аналитический расчет плоских ферм.

Фермой называется жесткая конструкция из прямолинейных стержней, соединенных на концах шарнирами. Если все стержни фермы лежат в одной плоскости, ферма называется плоской. Места соединения стержней фермы называют узлами. Все внешние нагрузки к ферме прикладываются только в узлах. При расчете фермы трением в узлах и весом стержней (по сравнению с внешними нагрузками) пренебрегают или распределяют веса стержней по узлам.

Тогда на каждый из стержней фермы будут действовать две силы, приложен­ные к его концам, которые при равновесии могут быть направлены только вдоль стержня. Следовательно, можно считать, что стержни фермы работают только на растяжение или на сжатие. Огра­ничимся рассмотрением жестких плоских ферм, без лишних стержней, образованных из треугольников. В таких фермах число стержней k и число узлов n связаны соотношением

Расчет фермы сводится к определению опорных реакций и уси­лий в ее стержнях.

Опорные реакции можно найти обычными методами статики, рассматривая ферму в целом как твердое тело. Перейдем к определе­нию усилий в стержнях.

Метод вырезания узлов. Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к по­следовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов фермы. Ход расчетов поясним на конкретном примере.

Рис.23

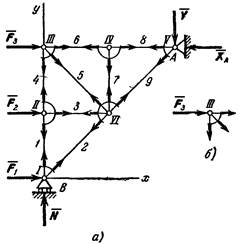
Рассмотрим изображенную на рис. 23,а ферму, образованную из одинаковых равнобедренных прямоугольных треугольников; действую­щие на ферму силы парал­лельны оси х и равны: F₁ = F₂ = F₃ = F = 2.

В этой ферме число узлов n = 6, а число стержней k = 9. Следовательно, соот­ношение выполняется и ферма является жесткой, без лишних стержней.

Составляя уравнения рав­новесия для фермы в целом, найдем, что реакции опор направлены, как пока­зано на рисунке, и численно равны;

Переходим к определению усилий в стержнях.

Пронумеруем узлы фермы римскими цифрами, а стержни — арабскими. Искомые усилия будем обозначать S₁ (в стержне 1), S₂ (в стержне 2) и т. д. Отрежем мысленно все узлы вместе со сходящимися в них стержнями от осталь­ной фермы. Действие отброшенных частей стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям S₁, S_2.

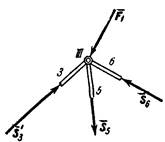
Изображаем сразу все эти силы на рисунке, направляя их от узлов, т. е. считая, все стержни растя­нутыми (рис. 23, а; изображенную картину надо представлять себе для каждого узла так, как это показано на рис. 23, б для узла III). Если в результате расчета величина усилия в каком-нибудь стержне получится отрицательной, это будет означать, что данный стержень не растянут, а сжат. Буквенных обозначений для сил, действующих вдоль стержней, ни рис. 23 не вводам, поскольку ясно, что силы, действующие вдоль стержня 1, равны численно S₁, вдоль стержня 2 — равны S₂ и т. д.

Теперь для сил, сходящихся в каждом узле, составляем последо­вательно уравнения равновесия:

Начинаем с узла 1, где сходятся два стержня, так как из двух уравнений равновесия можно определить только два неизвестных усилия.

Составляя уравнения равновесия для узла 1, получим

Отсюда находим:

Теперь, зная S₁, переходим к узлу II. Для него уравнения равнове­сия дают:

Определив S₄, составляем аналогичным путем уравнения равновесия сначала для узла III, а затем для узла IV. Из этих уравнений находим:

Наконец, для вычисления S₉ составляем уравнение равновесия сил, сходящихся в узле V, проектируя их на ось By. Получим Y_A + S₉cos45 0 = 0 откуда

Второе уравнение равновесия для узла V и два уравнения для узла VI можно составить как поверочные. Для нахождения усилий в стержнях эти уравнения не понадобились, так как вместо них были использованы три уравнения равновесия всей фермы в целом при определении N, Х_А, и Y_А.

Окончательные результаты расчета можно свести в таблицу:

№ стержня
Усилие в Н	-1	-2,82	-2	-1	+1,41	-3	-3	-4,23

Как показывают знаки усилий, стержень 5 растянут, остальные стер­жни сжаты; стержень 7 не нагружен (нулевой, стержень).

Наличие в ферме нулевых стержней, подобных стержню 7, обна­руживается сразу, так как если в узле, не нагруженном внешними силами, сходятся три стержня, из которых два направлены вдоль одной прямой, то усилие в третьем стержне равно нулю. Этот результат получается из уравнения равновесия в проекции на ось, перпендикулярную к упомянутым двум стержням.

Если в ходе расчета встретится узел, для которого число неизве­стных больше двух, то можно воспользоваться методом сечений.

Метод сечений (метод Риттера). Этим методом удобно поль­зоваться для определения усилий в отдельных стержнях фермы, в ча­стности, для проверочных расчетов. Идея метода состоит в том, что ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилие, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е. считая стержни рас­тянутыми (как и в методе вырезания узлов). Затем составляют урав­нения равновесия, беря центры моментов (или ось проекций) так, чтобы в каждое уравнение вошло только одно неизвестное усилие.

Графический расчет плоских ферм.

Расчет фермы мето­дом вырезания узлов может производиться графически. Для этого сначала, определяют опорные реакции. Затем, последовательно отсекая от фермы каждый из ее узлов, нахо­дят усилия в стержнях, сходящихся в этих узлах, строя соответствую­щие замкнутые силовые многоугольники. Все построения проводятся в масштабе, который должен быть заранее выбран. Рас­чет начинают с узла, в котором сходятся два стержня (иначе не удастся определить неизвест­ные усилия).

Рис.24

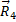
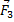
В качестве примера рас­смотрим ферму, изображен­ную на рис. 24, а. В этой ферме число узлов n = 6, а число стержней k = 9. Следовательно, соотношение выполняется и ферма является жесткой, без лиш­них стержней. Опорные реак­ции и для рассматри­ваемой фермы, изображаем на­ряду с силами и , как известные.

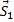
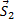
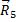
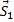
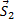
Определение усилий в стержнях начинаем с рас­смотрения стержней, сходя­щихся в узле I (узлы нуме­руем римскими цифрами, а стержни — арабскими). Мысленно отрезав от этих стержней остальную часть фермы, отбрасываем ее действие отброшенной части также мысленно заменяем силами и , которые должны быть направлены вдоль стержней 1 и 2. Из сходящихся в узле I сил , и строим замкнутый треугольник (рис. 24, б).

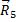
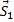
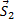
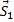
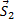
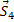
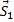
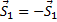
Для этого изображаем сначала в выбранном масштабе известную силу , а затем проводим через ее начало и конец прямые, параллельные стерж­ням 1 и 2. Таким путем будут найдены силы и , действующие на стержни 1 и 2. Затем рассматриваем равновесие стержней, сходящихся в узле II. Действие на эти стержни отброшенной части фермы мысленно заменяем силами , , и , направленными вдоль соответствующих стержней; при этом сила нам известна, так как по равенству дей­ствия и противодействия .

Построив из сил, сходящихся в узле II, замкнутый треугольник (начиная с силы 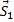), найдем вели­чины S₃ и S₄ (в данном случае S₄ = 0). Аналогично находятся усилия в остальных стержнях. Соответствующие силовые многоугольники для всех узлов показаны на рис. 24, б. Последний много­угольник (для узла VI) строится для про­верки, так как все входящие в него силы уже найдены.

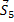
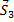
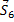
Из построенных многоугольников, зная масштаб, находим величины всех усилий. Знак усилия в каждом стержне опреде­ляется следующим образом. Мысленно вы­резав узел по сходящимся в нем стержням (например, узел III), прикладываем к обрезам стержней найденные силы (рис. 25); сила, направленная от узла ( на рис. 25), растягивает стержень, а си­ла, направленная к узлу ( и на рис. 25) сжимает его.

Рис.25

Соглас­но принятому условию растягивающим усилиям приписываем знак «+», а сжимающим — знак «-». В рассмотренном примере (pиc. 25) стержни 1, 2, 3, 6, 7, 9 сжаты, а стержни 5, 8 растянуты.

Источник