- Графический метод (метод корреляционного поля)
- Метод корреляционного анализа: пример. Корреляционный анализ — это.
- Понятие о корреляционном анализе
- Понятие о ложности корреляции
- Задачи корреляционного анализа
- Связь корреляционного анализа с регрессионным
- Условия использования метода
- Правила отбора факторов корреляционного анализа
- Отображение результатов
- Трехмерное представление диаграммы разброса (рассеивания)
- Оценка тесноты связи
- Пример применения метода корреляционного анализа
- Использование ПО при проведении корреляционного анализа
- В заключение
Графический метод (метод корреляционного поля)
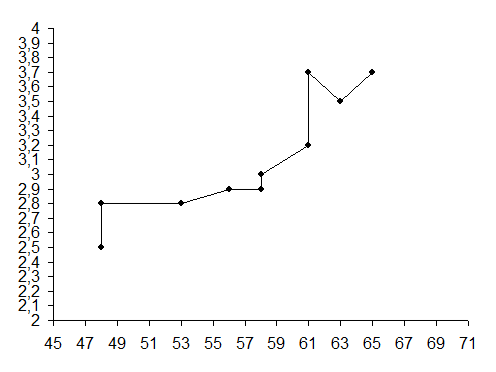
Графический метод часто называют методом корреляционного поля. Сущность его заключается в следующем: на график, у которого одна ось х – признак-фактор, а другая ось у – признак-результат, наносятся точки, отображающие исходную информацию (удобнее в ранжированном виде, по таблице 10.2), и соединяются ломаной линией. Далее по расположению этих точек на графике делается вывод о наличии, направлении и, частично, о тесноте связи:
а) если точки на графике концентрируются около некоторой прямой, направленной из левого нижнего в правый верхний угол, то принимается вывод о наличии прямой связи (связь есть, связь прямая);
б) если точки концентрируются около прямой, направленной из левого верхнего в правый нижний угол, связь есть и она обратная;
в) если точка концентрируется в виде дуги около некоторой кривой (например, параболы) принимается вывод о наличии криволинейной связи;
г) если на корреляционном поле наблюдается хаотичный разброс точек, принимается вывод об отсутствии взаимосвязи исследуемых признаков.
Примерный вывод о тесноте связи делается на основании разброса точек на корреляционном поле. Чем ближе они концентрируются вокруг некоторой прямой или кривой, т.е. чем меньше их рассеяние, тем теснее корреляционная связь.
В нашем примере (рисунок 10.1) точки на корреляционном поле концентрируются около прямой, направленной из левого нижнего в правый верхний угол, что позволяет сделать вывод о наличии прямой зависимости между фондоотдачей и удельным весом активной части в общей стоимости основных средств. Более того, точки сконцентрированы достаточно близко к некоторой прямой.
Рисунок 10.1 – Корреляционное поле зависимости фондоотдачи (у) от удельного веса активной части основных средств (x)
Вывод: связь есть, связь прямая и достаточно тесная.
Балансовый метод
Этот метод имеет и целый ряд других названий: табличный метод, метод корреляционной таблицы, метод корреляционной решетки.
Для построения такой таблицы (она имеет форму шахматной таблицы), группируются уровни х и у исходя из следующих правил:
— интервалы устанавливаются равные, т.е. ширина интервала определяется по формуле:
для признака-фактора 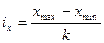
для признака-результата 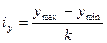
— количество групп (k) одинаковое для х и для у;
— количество интервалов не следует делать большим, т.к. таблица теряет наглядность (хотя строгих правил нет).
В нашем примере примем k = 4, тогда
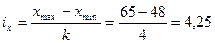
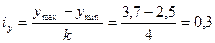
После этого строится макет корреляционной таблицы по строкам – признак-фактор, по столбцам – признак-результат.
 Группы предприя- тий по y Группы предприятий по х Группы предприя- тий по y Группы предприятий по х | 2,5 -2,8 | 2,8-3,1 | 3,1-3,4 | 3,4-3,7 | Всего |
| 48,00 — 52,25 | . | . | |||
| 52,25 – 56,50 | .. | ||||
| 56,50 – 60,75 | .. | ||||
| 60,75 – 65,00 | . | … | |||
| Всего |
Заполнение построенной таблицы производится методом точек или черточек: на пересечении соответствующей строки (х) и столбца (у) в любом месте квадрата (прямоугольника) ставится точка либо черточка. Иногда ставится число, показывающее общее количество единиц совокупности, которое попало в данный прямоугольник (в левом верхнем квадрате должна быть 1, а в правом нижнем – 3).
На последнем этапе производится анализ расположения единиц совокупности по группам, т.е. в таблице:
а) если точки впиваются в эллипс, направленный из левого верхнего в правый нижний угол, связь есть, и она прямая;
б) если точки вписываются в эллипс, направленный из левого нижнего в правый верхний угол, связь есть, и она обратная;
в) если точки концентрируются около некоторой дуги, делается предположение о наличии криволинейной связи;
г) при хаотичном разбросе данных принимается вывод об отсутствии связи между исследуемыми признаками.
В нашем примере точки в корреляционной таблице вписываются в эллипс, направленный из левого верхнего в правый нижний угол, следовательно, между фондоотдачей и удельным весом активной части основных средств существует прямая связь.
Дата добавления: 2016-01-16 ; просмотров: 1027 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Метод корреляционного анализа: пример. Корреляционный анализ — это.
В научных исследованиях часто возникает необходимость в нахождении связи между результативными и факторными переменными (урожайностью какой-либо культуры и количеством осадков, ростом и весом человека в однородных группах по полу и возрасту, частотой пульса и температурой тела и т.д.).
Вторые представляют собой признаки, способствующие изменению таковых, связанных с ними (первыми).
Понятие о корреляционном анализе
Существует множество определений термина. Исходя из вышеизложенного, можно сказать, что корреляционный анализ — это метод, применяющийся с целью проверки гипотезы о статистической значимости двух и более переменных, если исследователь их может измерять, но не изменять.
Есть и другие определения рассматриваемого понятия. Корреляционный анализ — это метод обработки статистических данных, заключающийся в изучении коэффициентов корреляции между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков, для установления между ними статистических взаимосвязей. Корреляционный анализ — это метод по изучению статистической зависимости между случайными величинами с необязательным наличием строгого функционального характера, при которой динамика одной случайной величины приводит к динамике математического ожидания другой.
Понятие о ложности корреляции
При проведении корреляционного анализа необходимо учитывать, что его можно провести по отношению к любой совокупности признаков, зачастую абсурдных по отношению друг к другу. Порой они не имеют никакой причинной связи друг с другом.
В этом случае говорят о ложной корреляции.
Задачи корреляционного анализа
Исходя из приведенных выше определений, можно сформулировать следующие задачи описываемого метода: получить информацию об одной из искомых переменных с помощью другой; определить тесноту связи между исследуемыми переменными.
Корреляционный анализ предполагает определение зависимости между изучаемыми признаками, в связи с чем задачи корреляционного анализа можно дополнить следующими:
- выявление факторов, оказывающих наибольшее влияние на результативный признак;
- выявление неизученных ранее причин связей;
- построение корреляционной модели с ее параметрическим анализом;
- исследование значимости параметров связи и их интервальная оценка.
Связь корреляционного анализа с регрессионным
Условия использования метода
Результативные факторы зависят от одного до нескольких факторов. Метод корреляционного анализа может применяться в том случае, если имеется большое количество наблюдений о величине результативных и факторных показателей (факторов), при этом исследуемые факторы должны быть количественными и отражаться в конкретных источниках. Первое может определяться нормальным законом — в этом случае результатом корреляционного анализа выступают коэффициенты корреляции Пирсона, либо, в случае, если признаки не подчиняются этому закону, используется коэффициент ранговой корреляции Спирмена.
Правила отбора факторов корреляционного анализа
При применении данного метода необходимо определиться с факторами, оказывающими влияние на результативные показатели. Их отбирают с учетом того, что между показателями должны присутствовать причинно-следственные связи. В случае создания многофакторной корреляционной модели отбирают те из них, которые оказывают существенное влияние на результирующий показатель, при этом взаимозависимые факторы с коэффициентом парной корреляции более 0,85 в корреляционную модель предпочтительно не включать, как и такие, у которых связь с результативным параметром носит непрямолинейный или функциональный характер.
Отображение результатов
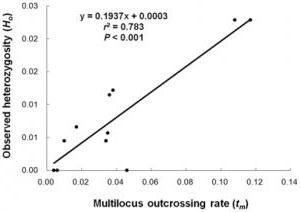
Результаты корреляционного анализа могут быть представлены в текстовом и графическом видах. В первом случае они представляются как коэффициент корреляции, во втором — в виде диаграммы разброса.
При отсутствии корреляции между параметрами точки на диаграмме расположены хаотично, средняя степень связи характеризуется большей степенью упорядоченности и характеризуется более-менее равномерной удаленностью нанесенных отметок от медианы. Сильная связь стремится к прямой и при r=1 точечный график представляет собой ровную линию. Обратная корреляция отличается направленностью графика из левого верхнего в нижний правый, прямая — из нижнего левого в верхний правый угол.
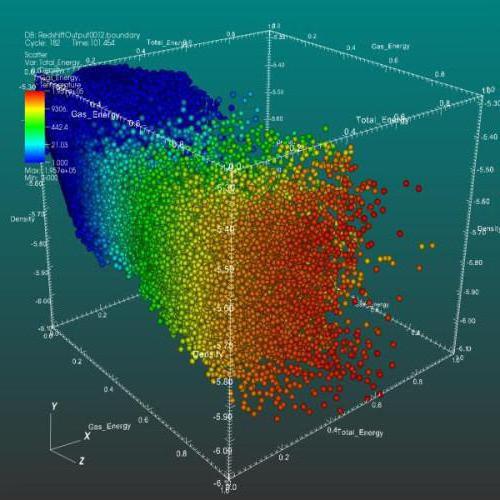
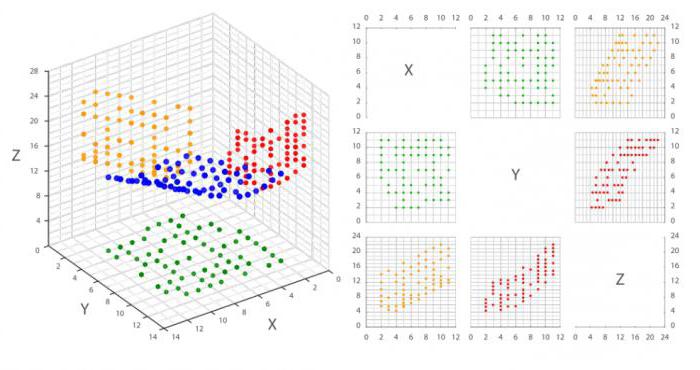
Трехмерное представление диаграммы разброса (рассеивания)
Помимо традиционного 2D-представления диаграммы разброса в настоящее время используется 3D-отображение графического представления корреляционного анализа.
Также используется матрица диаграммы рассеивания, которая отображает все парные графики на одном рисунке в матричном формате. Для n переменных матрица содержит n строк и n столбцов. Диаграмма, расположенная на пересечении i-ой строки и j-ого столбца, представляет собой график переменных Xi по сравнению с Xj. Таким образом, каждая строка и столбец являются одним измерением, отдельная ячейка отображает диаграмму рассеивания двух измерений.
Оценка тесноты связи
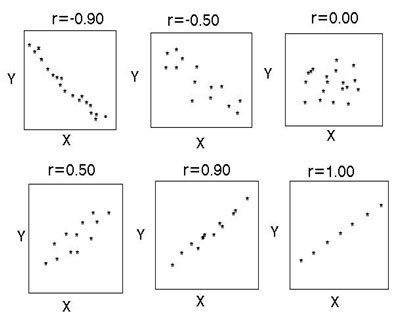
Теснота корреляционной связи определяется по коэффициенту корреляции (r): сильная — r = ±0,7 до ±1, средняя — r = ±0,3 до ±0,699, слабая — r = 0 до ±0,299. Данная классификация не является строгой. На рисунке показана несколько иная схема.
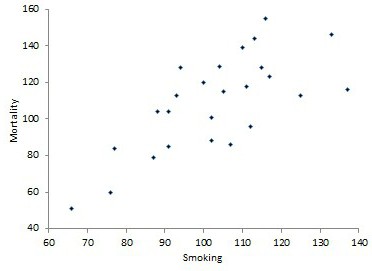
Пример применения метода корреляционного анализа
В Великобритании было предпринято любопытное исследование. Оно посвящено связи курения с раком легких, и проводилось путем корреляционного анализа. Это наблюдение представлено ниже.