Способы задания функции
Основной признак функциональной зависимости между двумя переменными величинами — это наличие соответствия между значениями этих величин: каждому допустимому значению одной переменной соответствует строго определённое значение другой.
Функция считается заданной, как только установлено соответствие между двумя переменными. Это соответствие может быть установлено различными способами. Рассмотрим подробнее три из них: аналитический, табличный и графический.
Аналитический способ
Аналитический способ — это способ задания функции с помощью формулы.
Например, формула y = x — 2 показывает, как с помощью значения аргумента x вычислить соответствующее ему значение функции y.
Табличный способ
Табличный способ — это способ задания функции с помощью таблицы со значениями.
Например, если измерять температуру воздуха каждый час в течении суток, то каждому часу (t) будет соответствовать определённая температура (T). Такое соответствие можно записать в виде таблицы:
| t (ч) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T (°) | 14 | 14 | 14,5 | 14,5 | 15 | 15 | 16 | 16 | 16 | 16,5 | 16,5 | 17 |
| t (ч) | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| T (°) | 18 | 20 | 22 | 24 | 24,5 | 24,5 | 24 | 23 | 21 | 20 | 18 | 16 |
Следовательно, T функция от t — T(t) , определённая с помощью множества целых чисел от 0 до 24 и заданная таблицей. Соответствие между величинами двух переменных задаётся в данном случае не формулой, а таблицей.
Графический способ
Графический способ — это способ задания функции с помощью графика. В этом случае аргумент является абсциссой точки, а значение функции, соответствующее данному аргументу, ординатой.
Графики позволяют быстро находить значение функции по значению аргумента и наоборот — значение аргумента по значению функции. Например, рассмотрим уже готовый график функции:
Чтобы узнать, какое значение функции будет соответствовать аргументу x = 1, надо провести из соответствующей точки оси абсцисс (оси x) перпендикуляр на график. Ордината точки пересечения перпендикуляра с графиком (точки M) и будет соответствующим значением функции. Поэтому, так как точка M имеет координаты (1; 2), то запись этих значений в виде функции будет выглядеть так: y(1) = 2.
Источник
Аналитический метод решения
При аналитическом методе решения отправляются не от условия задачи, как это делают при синтетическом методе, а от ее требования, вопроса. Это характерно для всех разновидностей аналитического метода, применяемых при решении задач.
Решение задач аналитическим методом начинается с постановки следующего вопроса, связанного с требованием решаемой задачи: «Что нужно знать, чтобы ответить на вопрос данной задачи (выполнить требование)?» Для правильного ответа на поставленный вопрос необходимо знать данные задачи и учитывать те зависимости, которые связывают их с искомым числом.
Пусть для вычисления искомого Y основной задачи требуется знать, например, числа p1 и q1, из которых при помощи некоторого математического действия можно получить Y, т.е. решить основную задачу. Итак, основная задача с требованием Y преобразовалась в первую серию вспомогательных задач с искомыми p1 и q1. Обозначим первую серию вспомогательных задач через В1. Ставим тот же вопрос к каждой из вспомогательных задач: «Что нужно знать, чтобы найти p1 (q1)?» и опять при ответе на этот вопрос используем условие А основной задачи, а также арсенал математической теории.
Пусть для вычисления p1 нужно знать p2 и q2, а для вычисления q1 – знать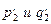 
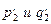
. Теперь основная задача преобразовалась во вторую серию (В2) вспомогательных задач, включающих задачи по нахождению p2, q2, .
Продолжая процесс преобразования, получаем, наконец, такую серию (Вn) вспомогательных задач, искомые которых содержатся во множестве данных основной задачи.
Итак основная задача решена аналитическим методом, поскольку этим методом проведен поиск и найден путь решения задачи; главное здесь именно в этом, а не в оформлении записи уже известного решения.
Найденное аналитическое решение можно изложить различными способами, в том числе и синтетическим. В последнем случае пришлось бы следовать от конца аналитического рассуждения к его началу, не производя при этом никаких поисков.
Если основную задачу условно записать формулой А 
У, описанный выше аналитический путь преобразования задачи изобразится схемой:
,
Где А Вn, Вn Bn-1, . . . , В1 У, откуда А У.
К рассмотренной в предыдущем пункте текстовой задаче применим аналитический метод решения. Наличие двух искомых в задаче несколько осложняет построение рассуждений, поэтому можно ограничиться сначала одним искомым, найти его и затем воспользоваться им как уже известным числом при отыскании пути получения второго искомого. Рассмотрим схему:
- За сколько часов может выполнить всю работу, работая отдельно, та машина, которая продолжила работу?
- Часть всей работы, выполненная этой машиной.
- Сколько часов работала эта машина отдельно когда она работала отдельно
- Объем всей работы
- Часть всей работы, выполненная двумя машинами совместно
- За сколько часов машины вместе Выполнят всю работу?
- Сколько часов они работали совместно?
Такой поиск обычно проводится устно и завершается составлением плана решения. Аналогично теперь можно построить схему аналитического поиска второго числа основной задачи (сделайте самостоятельно!).
В практике решения задач методы анализа и синтеза полностью разделить, изолировать друг от друга невозможно. Они полезно сочетаются. При аналитическом методе имеют место скрытые элементы синтеза. Например, преобразуя требование основной задачи в требования первой серии вспомогательных задач, мы неявно проверяем правильность этого преобразования, возможность синтезирования из искомых чисел задач первой серии искомого основной задачи.
Широкое применение находит аналитический метод при решении геометрических задач на вычисление. Здесь удобно начинать решение с соответствующей формулы, которая и показывает, какой будет первая серия вспомогательных задач и т.д. Кратко продемонстрируем это на примере следующей геометрической задачи.
Задача. В конус вписана пирамида, основанием которой служит прямоугольный треугольник и боковая грань которой, проходящая через один из катетов основания, образует с плоскостью основания двугранный угол α. Найти объем пирамиды, если образующая конуса равна l и наклонена к плоскости основания под углом β.
Р е ш е н и е. Начертим конус с вписанной в него пирамидой МАВС, в которой длины боковых ребер МА = МВ = МС = l, АС – гипотенуза треугольника АВС, центр основания конуса – точка О, Ао = ОС, ÐМАО=β, ÐМDО = α.
Формула объема пирамиды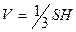 
. Задача сводится к нахождению площади основания S и высоты H = MO. (Первая серия из двух вспомогательных задач; последнюю из этих задач можно решить по имеющимся данным.).
Из прямоугольного треугольника ОМА находим Н = ОМ = lsinβ.
Для нахождения площади основания надо найти длины катетов АВ и ВС. (Получаем вторую серию из двух вспомогательных задач.)
Для определения АВ достаточно найти ОD – длину средней линии треугольника АВС, а для вычисления ВС надо найти АС ( третья серия из двух вспомогательных задач; решение первой задачи уже известно):
OD = MO ctgα = l sinβ ctg α.
Для получения АС достаточно знать АО ( четвертая серия – одна задача, которую можно решить):
; 
; 
;
;
;
.
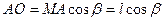
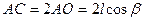
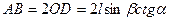
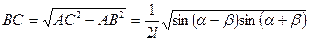
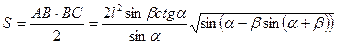
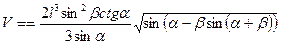
Приведенное решение является очень кратким (отсутствуют выкладки, обоснования), чтобы выделить метод решения. Учащиеся, чтобы научиться решать задачи, должны делать полные математические выкладки и уметь обосновывать каждый свой шаг в процессе решения ссылкой на условие задачи или изученную математическую теорию.
Хотя путь поиска на основе аналитического метода решения не всегда однозначен, однако он все же менее многозначен и более определен, чем путь поиска при синтетическом методе решения. Аналитический метод удобен для поиска пути решения новой для учащихся задачи, он опирается на определенное умение школьника рассуждать и эффективно способствует развитию его продуктивного, логического и функционального мышления. В результате систематического применения аналитического метода решения задач у учащихся быстрее формируется умение cамостоятельно решать новые для них задачи, чем при пользовании синтетическим методом.
Источник
Функция. Способы задания функций.
Функция является заданной, иначе говоря, известной, если для каждого значения возможного числа аргументов можно узнать соответствующее значение функции. Наиболее распространенные три способа задания функции: табличный, графический, аналитический, существуют еще словесный и рекурсивный способы.
1. Табличный способ наиболее широко распространен (таблицы логарифмов, квадратных корней), основное его достоинство – возможность получения числового значения функции, недостатки заключаются в том, что таблица может быть трудно читаема и иногда не содержит промежуточных значений аргумента.
Аргумент х принимает заданные в таблице значения, а у определяется соответственно этому аргументу х.
2. Графический способ заключается в проведении линии (графика), у которой абсциссы изображают значения аргумента, а ординаты – соответствующие значения функции. Часто для наглядности масштабы на осях принимают разными.
Например: для нахождения по графику у, которому соответствует х = 2,5 необходимо провести перпендикуляр к оси х на отметке 2,5. Отметку можно довольно точно сделать с помощью линейки. Тогда найдем, что при х = 2,5 у равно 7,5, однако если нам необходимо найти значение у при х равном 2,76, то графический способ задания функции не будет достаточно точным, т.к. линейка не дает возможности для столь точного замера.
Достоинства этого способа задания функций заключаются в легкости и целостности восприятия, в непрерывности изменения аргумента; недостатком является уменьшение степени точности и сложность получения точных значений.
3. Аналитический способ состоит в задании функции одной или несколькими формулами. Основным достоинством этого способа является высокая точность определения функции от интересующего аргумента, а недостатком является затрата времени на проведение дополнительных математических операций.
Функцию можно задать с помощью математической формулы y=x 2 , тогда если х равно 2, то у равно 4, возводим х в квадрат.
4. Словесный способ состоит в задании функции обычным языком, т.е. словами. При этом необходимо дать входные, выходные значения и соответствие между ними.
Словесно можно задать функцию (задачу), принимающуюся в виде натурального аргумента х с соответствующим значением суммы цифр, из которых состоит значение у. Поясняем: если х равно 4, то у равно 4, а если х равно 358, то у равен сумме 3 + 5 + 8, т. е 16. Далее аналогично.
5. Рекурсивный способ состоит в задании функции через саму себя, при этом значения функции определяются через другие ее же значения. Такой способ задания функции используется в задании множеств и рядов.
При разложении числа Эйлера задается функцией:
Ее сокращение приведено ниже:
При прямом расчёте возникает бесконечная рекурсия, но можно доказать, что значение f(n) при возрастании n стремится к единице (поэтому, несмотря на бесконечность ряда, значение числа Эйлера конечно). Для приближённого вычисления значения e достаточно искусственно ограничить глубину рекурсии некоторым наперёд заданным числом и по достижении его использовать вместо f(n) единицу.
Источник
