Прямое и обратное включение перехода
При использовании \(p\)-\(n\)-перехода в реальных полупроводниковых приборах к нему может быть приложено внешнее напряжение. Величина и полярность этого напряжения определяют поведение перехода и проходящий через него электрической ток. Если положительный полюс источника питания подключается к \(p\)-области, а отрицательный — к \(n\)-области, то включение называют прямым включением. При изменении указанной полярности включение \(p\)‑\(n\)‑перехода называют обратным включением.
При прямом включении \(p\)-\(n\)-перехода внешнее напряжение создает в переходе поле, которое противоположно по направлению внутреннему диффузионному электрическому полю. Напряженность результирующего поля падает, что сопровождается сужением запирающего слоя. В результате этого большое количество основных носителей зарядов получает возможность диффузионно переходить в соседнюю область (ток дрейфа при этом не изменяется, поскольку он зависит от количества неосновных носителей, появляющихся на границах перехода), т.е. через переход будет протекать результирующий ток, определяемый в основном диффузионной составляющей. Диффузионный ток зависит от высоты потенциального барьера и по мере его снижения увеличивается экспоненциально.
Повышенная диффузия носителей зарядов через переход приводит к повышению концентрации дырок в области \(n\)-типа и электронов в области \(p\)-типа. Такое повышение концентрации неосновных носителей вследствие влияния внешнего напряжения, приложенного к переходу, называется инжекцией неосновных носителей. Неравновесные неосновные носители диффундируют вглубь полупроводника и нарушают его электронейтральность. Восстановление нейтрального состояния полупроводника происходит за счет поступления носителей зарядов от внешнего источника. Это является причиной возникновения тока во внешней цепи, называемого прямым током.
При включении \(p\)-\(n\)-перехода в обратном направлении внешнее обратное напряжение создает электрическое поле, совпадающее по направлению с диффузионным, что приводит к росту потенциального барьера и увеличению ширины запирающего слоя. Все это уменьшает диффузионные токи основных носителей. Для неосновных носителе поле в \(p\)-\(n\)-переходе остается ускоряющим, и поэтому дрейфовый ток не изменяется.
Таким образом, через переход будет протекать результирующий ток, определяемый в основном током дрейфа неосновных носителей. Поскольку количество дрейфующих неосновных носителей не зависит от приложенного напряжения (оно влияет только на их скорость), то при увеличении обратного напряжения ток через переход стремиться к предельному значению \(I_S\) , которое называется током насыщения. Чем больше концентрация примесей доноров и акцепторов, тем меньше ток насыщения, а с увеличением температуры ток насыщения растет по экспоненциальному закону.
Источник
4.6. Толщина р-n перехода
Рассмотрим резкий электронно-дырочный переход, то есть переход, в котором область изменения примесей значительно меньше области пространственного заряда.
До сих пор мы рассматривали симметричные переходы, то есть переходы, в которых концентрации доноров и акцепторов в n— и р-областях одинаковы. В реальных переходах удельные сопротивления р— и n-областей, и, следовательно, концентрации примесей в них отличаются на 2…3 порядка величины. Это приводит к тому, что переход смещается в сторону области с более высоким сопротивлением.
Для определенности будем полагать, что эмиттером является n-область, а базой – р-область. В большинстве практических случаев выполняется неравенство 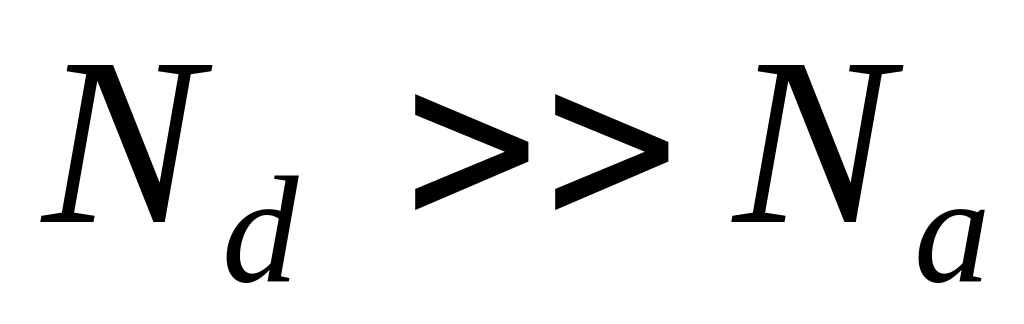

В толще эмиттера и базы концентрации основных носителей заряда практически совпадают с результирующими концентрациями примеси, а концентрации неосновных носителей определяются законом действующих масс. При этом концентрация неосновных носителей в базе больше, чем в эмиттере.
Переход занимает область в пределах –ln0 > Nd, можно считать, что переход полностью лежит в донорной области и концентрацией акцепторов пренебречь. Тогда толщину перехода можно определить по упрощенной формуле

Если имеется обратное соотношение Nd >> Nа, то формула принимает вид
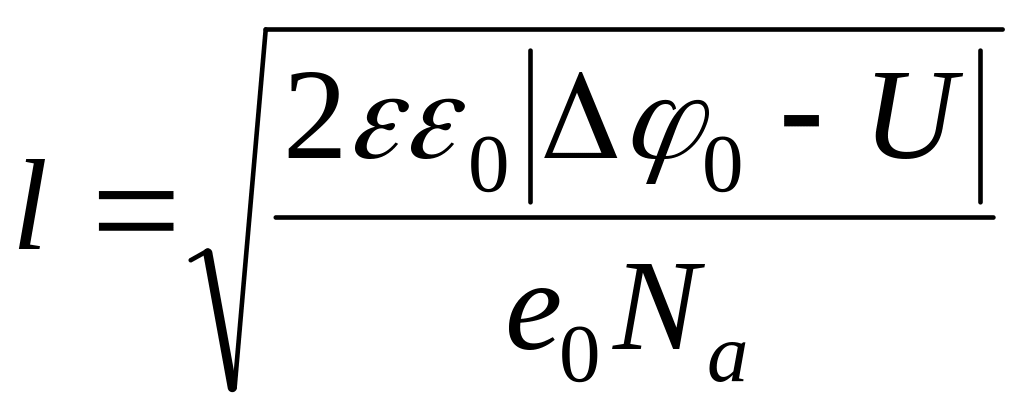
С уменьшением концентрации примесей толщина перехода возрастает. При прямом напряжении толщина перехода уменьшается, при обратном – увеличивается.
Источник
Электронно-дырочный переход в состоянии равновесия
Электронно-дырочный или это контакт между областями полупроводника n- и p-типа. Электронно-дырочный переход создается в одном кристалле полупроводника в основном при помощи трех технологических операций. Это сплавная технология (в настоящее время не применяется), инжектирование примесей и эпитаксия (наращивание) дополнительных слоев атомов на поверхность кристалла. Этот способ позволяет получить наиболее качественные , так как при этом можно достаточно точно регулировать концентрацию примесей в объеме полупроводникового материала.
Рассмотрим электронно-дырочный переход, в котором концентрации доноров Nд и акцепторов Na изменяются скачком на границе раздела, как это показано на рисунке 1а. Такой p-n переход называют резким. Его можно получить наращиванием дополнительных слоев атомов на поверхности полупроводникового кристалла. Инжекция примесей из газообразной среды формирует плавный p-n переход. В нем концентрация примесей растет при приближении к поверхности кристалла и снижается при удалении от неё.
Рисунок 1. Равновесное состояние p-n перехода
Концентрация «дырок» в p-области полупроводника pp0 значительно превышает их концентрацию в n-области pn0. Аналогично для электронов в n-области выполняется условие . Неравномерное распределение концентрации носителей зарядов в полупроводниковом кристалле в районе p-n перехода, показанное на приводит к возникновению диффузии электронов из n-области в p-область и «дырок» из p-области в n-область.
Описанное движение зарядов через создает совместный диффузионный ток. С учетом выражений (3) и (4), приведенных в статье «диффузионный ток», плотность полного диффузионного тока, проходящего через электронно-дырочный переход, будет определяться суммой тока электронов и «дырок»:

Электроны и дырки, движущиеся из-за дифузии через p-n переход навстречу друг другу, рекомбинируют и в приконтактной области p-полупроводника образуется нескомпенсированный заряд отрицательных ионов акцепторных примесей, а в n-полупроводнике нескомпенсированный заряд положительных донорных ионов. Рекомбинация на показана зачеркнутым изображением электронов и «дырок». Эта ситуация иллюстрируется графиком, приведенным на . В результате описанного процесса диффузии основных зарядов электронный полупроводник заряжается положительно, а дырочный — отрицательно.
Теперь определим дрейфовый ток через pn-переход. Собственное электрическое поле является тормозящим для основных носителей заряда и ускоряющим для неосновных. Электроны p-области и дырки n-области полупроводника, совершая тепловое движение, попадают в пределы диффузионного электрического поля, увлекаются им и перебрасываются в противоположные области, образуя дрейфовый ток, или ток проводимости. Выведение неосновных носителей заряда через электронно-дырочный переход ускоряющим электрическим полем называется экстракцией носителей заряда.
Воспользуемся выражением (2) из статьи «дрейфовый ток» и учитывая, что , определим плотность полного дрейфового тока через границу раздела p- и n- областей:

Так как по закону сохранения энергии через изолированный полупроводник ток проходить не должен, между диффузионным и дрейфовым токами устанавливается динамическое равновесие:
Контактная разность потенциалов
Между областями с различными типами проводимости возникает собственное электрическое поле напряженностью Eсоб, показанное на . Оно создаётся двумя областями объемных зарядов с контактной разностью потенциалов Uк. Её изменение в зависимости от положения относительно p-n контакта показано на . За пределами области объемного заряда области полупроводника n- и р-типа остаются электрически нейтральными.
Потенциальная энергия электрона и электрический потенциал связаны соотношением . Поэтому образование нескомпенсированных объемных зарядов вызывает понижение энергетических уровней n-области и повышение энергетических уровней р-области полупроводника. Смещение энергетических зон прекратится, когда уровни Ферми n- области Wфn и р-области Wфp совпадут. Эта ситуация показана на графике энергетических зон , приведенном на .
Рисунок 2. Энергетические зоны полупроводника в районе p-n перехода
Совпадение уровней Ферми n- и p- областей соответствует установлению динамического равновесия между этими областями полупроводника и возникновению между ними потенциального барьера Uk:

Подстановка в это выражение результатов логарифмирования формул (1) из статей «Полупроводники с дырочной проводимостью» и «Полупроводники с электронной проводимостью» позволяет получить следующее равенство:

Из этого выражения видно, что контактная разность потенциалов Uk зависит от отношения концентраций носителей зарядов в р- и n-областях .
Если ввести параметр , то концентрацию неосновных носителей в зависимости от концентрации основных носителей можно записать в следующем виде:


Параметр φт получил название температурный потенциал. Он имеет большое значение при работе с полупроводниковыми электронными приборами и часто используется в расчетах параметров биполярных транзисторов. При комнатной температуре () температурный потенциал .
Выражения (6) и (7) пригодятся нам при определении вольтамперной характеристики .
Ширина
Ешё одним важным параметром является его ширина . Ширина нам потребуется при определении его ёмкости. В общем случае концентрации основных носителей в n— и не равны. Ширину запирающего слоя δ можно найти, решив уравнения Пуассона отдельно для n— и :


Задав для этих выражений следующие граничные условия:



получим значения потенциала для n— и вблизи :


В точке оба решения должны давать одинаковые значения φ и 



Из равенства (12) видно, что толщина слоев объемных зарядов в n— и обратно пропорциональна концентрациям примесей и в несимметричном запирающий слой расширяется в область с меньшей концентрацией примесей. Увеличение концентрации атомов примеси сужает запирающий слой, а уменьшение расширяет его. Это часто используется для придания полупроводниковым приборам требуемых свойств.
Дата последнего обновления файла 11.05.2020
Понравился материал? Поделись с друзьями!
- Электронные, квантовые приборы и микроэлектроника. Под редакцией Федорова Н. Д. — М.: Радио и связь, 1998. -560 с.
- Электронные приборы. Под редакцией Шишкина Г.Г. -М.: Энергоатомиздат, 1989.-496 с.
- Батушев В. А. Электронные приборы. -М.: Высшая школа, 1980. -383 с.
- Савиных В. Л. Физические основы электроники. Учебное пособие. — Новосибирск.: СибГУТИ, 2003. — 77 с.
- Глазачев А. В. Петрович В. П. Физические основы электроники. Конспект лекций — Томск: Томский политехнический университет, 2015.
Вместе со статьей «Электронно-дырочный переход в состоянии равновесия» читают:
Источник
1.2 Ширина p-n перехода. Ёмкость p-n перехода.
1.2 Ширина p — n перехода. Ёмкость p — n перехода.
Из-за ухода основных носителей заря да, электронов из n — области в р — область и дырок из р- области в n — область, и в результате их рекомбинации, граница между р и n полупроводниками обеднена носителями заряда, и её сопротивление велико по сравнению с сопротивлением остальных областей. Эта граничная область, обладающая большим сопротивлением, называется запорным слоем. По своей протяжённости запорный слой- это слой области пространственного заряда.
Ширина этой области зависит от концентрации донорных и акцепторных примесей в n – и р- полупроводниках.
Распределение потенциала в переходной области и ширину области объёмного заряда можно определить из решения уравнения Пуассона, связывающего потенциал поля с объёмной плотностью зарядов, создающих это поле: , где — объёмная плотность зарядов,
— относительная диэлектрическая проницаемость полупроводника, — диэлектрическая проницаемость вакуума. Из решения э того уравнения с учётом граничных условий на контакте можно получить выражение для определения контактной разности
d -ширина p — n перехода, т.е. суммарная ширина отрицательно заряжённой области р- полупроводника и положительно заряжённой области n — полупроводника d = x n + x p . Здесь -концентрации акцепторных и донорных примесей соответственно.
Если концентрация примесей в одной области значительно больше чем в другой, например, (так называемый несимметричный p — n переход ), выражение для определения ширины p — n перехода упрощается и принимает вид:
Так как = x n / x p , то np и x n >> x p и ширина области объёмного заряда распространяется в полупроводник с меньшей концентрацией примеси. Из анализа выражения для определения вытекает, что ширина области пространственного заряда, т.е. ширина p — n перехода тем больше, чем слабее легированы полупроводники, и наоборот, значение d тем меньше, чем больше концентрация донорных и акцепторных примесей. При получается симметричный p — n переход и области пространственного заряда одинаково удалены от границы контактов в обе стороны p — n перехода. Если же концентрация одной из примесей больше, тогда область пространственного заряда расположена в основном на стороне слаболегированного полупроводника. Приведённое выше выражение для ширины p — n перехода имеет место, если существует резкая граница между p и n — областями полупроводника. При плавных p — n переходах, когда концентрация примесей от р- и n — областей меняется линейно, по закону = A х, где А — градиент концентрации примесей, ширина p — n перехода может быть выражена так:
Двойной электрический слой, имеющиеся в области p — n перехода можно уподобить обкладкам заряжённого плоского конденсатора и ёмкость такого перехода может быть определена по формуле ёмкости плоского конденсатора: С= S / d , где S — площадь p — n перехода, d — ширина p — n перехода. Если к p — n переходу приложить внешнее электрическое поле, то в зависимости от направления этого поля оно или складывается с внутренним контактным полем или вычитается из него. При приложении к концам p — n — областей внешнего напряжения, всё оно будет падать на области объёмного заряда т.к. эта область обеднена носителями заряда и её сопротивление велико по сравнению с сопротивлением остальных участков. Если к р- области подключить плюс, к n -области минус от внешнего источника ЭДС, то знак внешней ЭДС противоположен знаку и потенциальный барьер уменьшится, т.е. уменьшится ширина p — n перехода. при .
Такая полярность внешнего напряжения называется прямой. При обратной полярности напряжения высота потенциального барьера растёт, ширина p — n перехода увеличивается (рис.1.2). Как уже отмечалось, в несимметричном p — n переходе это увеличение происходит в основном в сторону области с меньшей концентрацией примеси. Поскольку с изменением внешнего напряжения происходит и изменение ширины p — n перехода, то соответственно изменяется и ёмкость перехода. С учётом внешне го напряжения формула для расчета ёмкости имеет вид: C = S
для случая C = S
Эта ёмкость называется барьерной иди зарядной ёмкостью.
В отличие от барьерной ёмкости существует понятие диффузионная ёмкость p — n перехода, связанная с накоплением неосновных носителей на границе p — n перехода при прохождении тока в прямом направлений. Об этом будет сказано позже. Как видно из формулы для барьерной ёмкости ,
ёмкость растет с увеличением концентрации примесей. Последняя формула часто используется для определения концентрации примеси по экспериментальной зависимости 1/ C 2 = f ( V ), которая представляет собой прямую линию. Если напряжение на p — n переходе V = ,то 1/ C 2 = 0. Таким образом можно экспериментально измерить .
В p — n переходе с линейным распределением примеси, прямая линия получается для зависимости 1/ C 3 = f ( V ), откуда можно определить А и .
Рис.1.2. Изменение ширины p — n перехода при приложении прямого (а) и обратного (б) напряжения.
Источник







