Запиши сумму всех чисел разными способами

Запиши сумму всех чисел разными способами

Нажмите Ctrl+D , чтобы добавить сайт в избранное.

ГДЗ ответы по математике 3 класс 1 часть учебника Дорофеев, Миракова, Бука (Перспектива) — 47-я страница ответов по математике 3 класс 1 часть Дорофеев

Страница 47

4. Выпиши в первый столбик выражения, в которых нужно прибавить сумму к числу, а во второй — выражения, в которых нужно вычесть число из суммы. Найди значения всех выражений.

34 34
15 + (26 + 8)=49 (26 + 8) — 15=19
64 64
32 + (40 + 24)=96 (40+ 24) — 32=32
67 67
30+ (47 + 20)=97 (47 + 20) — 30=37

Попробуй разгадать закономерность, с помощью которой составлены эти выражения, и запиши недостающее выражение в первый столбик.

1-й столбик 15 + (26 + 8) = 15 + 34 = 49; 32 + (40 + 24) = 32 + 64 = 96; 30 + (47 + 20) = 30 + 67 = 97.
2-й столбик. (26 + 8) – 15 = 34 – 15 = 19; (40 + 24) – 32 = 64 – 32 = 32; (47 + 20) – 30 = 67 – 30 = 37.

5. Составь задачу по каждой схематической записи. Реши задачи.

1) Было — 40 м провода 2) Было — 40 л бензина
Израсходовали — 15 м и 9 м Добавили — 15 л
Осталось — ? Израсходовали — 9 л
Стало — ?

Сравни условия и решения этих задач. Объясни, чем они похожи и чем различаются.

1) Из 40 м провода израсходовали 15 м, а затем еще 9 м. Сколько провода осталось?
Ответ: 40 – (15 + 9) = 40 – 24 = 16 м

2) В 40 л бензина добавили 15 л, затем израсходовали 9 л. Сколько бензина стало? Ответ: (40 + 15) – 9 = 55 – 9 = 46 л Задачи похожи условием, но различаются действием – добавили.

6. Измерь длины сторон данных многоугольников в сантиметрах. Вычисли периметр каждого многоугольника. Сравни результаты.

Для треугольника: измерить и сложить стороны KL + LM + MK; квадрат: (PO + PR) * 2.

7. Летом на даче собрали с 4 кустов смородину, по 3 кг ягод с каждого куста. Всю собранную смородину разложили в пакеты, по 2 кг в каждый. Сколько для этого понадобилось пакетов?

Всего собрали: 4 * 3 = 12 кг смородины. Понадобилось: 12 : 2 = 6 пакетов.

8. Произведение двух чисел больше одного из них в 2 раза и больше другого в 7 раз. Попробуй найти произведение этих чисел.

Запишем: 2 * 7 = 14. Произведение 14 : 7 = 2, больше одного в два раза и 14 : 2 = 7, больше другого в 7 раз.

Источник

Калькулятор суммы последовательных чисел

Все числа характеризуются свойствами делимости или факторизации, но кроме этого существуют числа, которые легко представить в виде суммы последовательных натуральных чисел.

Разложение чисел на составляющие

В теории чисел каждое натуральное число легко представить в виде составляющих. Разложение элементов натурального множества на простые множители позволяет выразить числа в виде произведения составляющих. Простые множители — это элементы целого ряда, которые делятся только на себя и на единицу, но их произведение формирует искомое число. Например, 50 легко разбить на неделимые и записать его в виде 2 × 5 × 5. Однако числа можно представлять не только в виде произведения, но и в форме суммы.

Совершенные числа

Наиболее известным примером выражения натуральных чисел в виде суммы являются совершенные и последовательные числа. Совершенные числа представляют собой математические объекты, которые записываются в виде суммы собственных делителей. Например, к таким объектам относятся 6 и 28:

• при разложении 6 на делители получаем 1, 2 и 3, что в сумме дает 6;
• разложив 28 на делители, мы получим 1, 2, 4, 7, 14, что при сложении дает 28.

По мере того, как натуральный ряд растет, совершенные числа встречаются все реже. Первые шесть членов совершенной последовательности выглядят так:

6, 28, 496, 8 128, 33 550 336, 8 589 869 056.

Очевидно, что совершенных чисел не так много, а математикам до сих пор неизвестно, существуют ли их предел или совершенная последовательность устремляется в бесконечность.

Последовательные числа

Последовательные числа записываются в виде суммы последовательных членов натурального ряда. Натуральный ряд — это положительные целые числа, которые мы используем при счете предметов. Последовательные члены ряда — это два рядом стоящих элемента, к примеру, 2 и 3, 17 и 18, 178 и 179.

Достаточно много натуральных чисел мы можем записывать в виде суммы последовательных элементов. Например, число 57 мы можем записать в трех вариантах:

• 7 + 8 + 9 + 10 + 11 + 12 = 57;
• 18 + 19 + 20 = 57;
• 28 + 29 = 57.

Точно также легко записать 58, 59, 60 и далее, а вот 64 последовательным числом не является и его невозможно представить в виде суммы последовательных членов натурального ряда.

Наш онлайн-калькулятор позволяет представить натуральные числа в виде суммы последовательных. Как видно, выразить число в виде суммы можно несколькими способами, поэтому наша программа высчитывает только один способ, который раскладывает число на сумму наибольшего количества слагаемых.

Примеры

Суммирование последовательных чисел

В работе с последовательными элементами натурального ряда существует несколько хитростей. Первая из таких уловок — это сложение пяти последовательных чисел быстрым способом, который состоит в умножении на 5 третьего члена последовательности. Например, если мы хотим быстро сложить 1 + 2 + 3 + 4 + 5, нам достаточно умножить 3 на 5 и получить 15. Давайте проверим и введем 15 в форму онлайн-калькулятора:

15 = 1 + 2 + 3 + 4 + 5.

Если мы возьмем следующую сумму из пяти последовательных чисел, например, 10 + 11 + 12 + 13 + 14, то умножив третий член на 5, мы получим 12 × 5 = 60. Проверим число 60 на возможность разложения в последовательный ряд:

• 60 = 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11;
• 60 = 10 + 11 + 12 + 13 + 14;
• 60 = 19 + 20 + 21.

Как видите, число 60 легко разложить на сумму тремя способами, среди которых есть и наш, который выражен в виде суммы пяти последовательных чисел.

Разложение чисел на сумму последовательных элементов

Для решения такой задачи от вас потребуется только ввести число в форму калькулятора. Давайте попробуем разложить на последовательные слагаемые большие числа:

• 256 — не последовательное число;
• 404 = 47 + 48 + 49 + 50 + 51 + 52 + 53 + 54;
• 666 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 + 21 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 30 + 31 + 32 + 33 + 34 + 35 + 36.

Таким образом, вы можете разложить достаточно большое количество членов натурального ряда, так как не последовательные числа встречаются довольно редко.

Заключение

Теория чисел — чистая математика, которую трудно использовать в повседневной жизни. Несмотря на это, вы можете использовать нашу программу для исследования самых разных свойств чисел.

Источник

Запиши сумму всех чисел разными способами

Нажмите Ctrl+D , чтобы добавить сайт в избранное.

ГДЗ ответы по математике 3 класс 1 часть учебника Дорофеев, Миракова, Бука (Перспектива) — 47-я страница ответов по математике 3 класс 1 часть Дорофеев

Страница 47

4. Выпиши в первый столбик выражения, в которых нужно прибавить сумму к числу, а во второй — выражения, в которых нужно вычесть число из суммы. Найди значения всех выражений.

34 34
15 + (26 + 8)=49 (26 + 8) — 15=19
64 64
32 + (40 + 24)=96 (40+ 24) — 32=32
67 67
30+ (47 + 20)=97 (47 + 20) — 30=37

Попробуй разгадать закономерность, с помощью которой составлены эти выражения, и запиши недостающее выражение в первый столбик.

1-й столбик 15 + (26 + 8) = 15 + 34 = 49; 32 + (40 + 24) = 32 + 64 = 96; 30 + (47 + 20) = 30 + 67 = 97.
2-й столбик. (26 + 8) – 15 = 34 – 15 = 19; (40 + 24) – 32 = 64 – 32 = 32; (47 + 20) – 30 = 67 – 30 = 37.

5. Составь задачу по каждой схематической записи. Реши задачи.

1) Было — 40 м провода 2) Было — 40 л бензина
Израсходовали — 15 м и 9 м Добавили — 15 л
Осталось — ? Израсходовали — 9 л
Стало — ?

Сравни условия и решения этих задач. Объясни, чем они похожи и чем различаются.

1) Из 40 м провода израсходовали 15 м, а затем еще 9 м. Сколько провода осталось?
Ответ: 40 – (15 + 9) = 40 – 24 = 16 м

2) В 40 л бензина добавили 15 л, затем израсходовали 9 л. Сколько бензина стало? Ответ: (40 + 15) – 9 = 55 – 9 = 46 л Задачи похожи условием, но различаются действием – добавили.

6. Измерь длины сторон данных многоугольников в сантиметрах. Вычисли периметр каждого многоугольника. Сравни результаты.

Для треугольника: измерить и сложить стороны KL + LM + MK; квадрат: (PO + PR) * 2.

7. Летом на даче собрали с 4 кустов смородину, по 3 кг ягод с каждого куста. Всю собранную смородину разложили в пакеты, по 2 кг в каждый. Сколько для этого понадобилось пакетов?

Всего собрали: 4 * 3 = 12 кг смородины. Понадобилось: 12 : 2 = 6 пакетов.

8. Произведение двух чисел больше одного из них в 2 раза и больше другого в 7 раз. Попробуй найти произведение этих чисел.

Запишем: 2 * 7 = 14. Произведение 14 : 7 = 2, больше одного в два раза и 14 : 2 = 7, больше другого в 7 раз.

Источник

Сумма разрядных слагаемых

О чем эта статья:

Сумма разрядных слагаемых

Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых. Сумму разрядных слагаемых можно записать следующим образом:

• Число 35 состоит из 3 десятков и 5 единиц

35 = 3 десятка + 5 единиц = 3*10 = 30 + 5 = 35.

30 — разрядное слагаемое; 5 — разрядное слагаемое.

• Число 86 состоит из 8 десятков и 6 единиц

86 = 8 десятков + 6 единиц = 8*10 = 80 + 6 = 86

80 — разрядное слагаемое; 5 — разрядное слагаемое.

• Число 356 состоит из 3 сотен, 5 десятков и 6 единиц

356 = 3 сотни + 5 десятков + 6 единиц = 3*100 + 5*10 + 6 = 300+50+6 = 356.

300, 50, 6 — разрядные слагаемые.

Разряды и классы чисел

Чтобы без труда записывать числа в виде суммы разрядных слагаемых, нужно безошибочно определять класс и разряд числа.

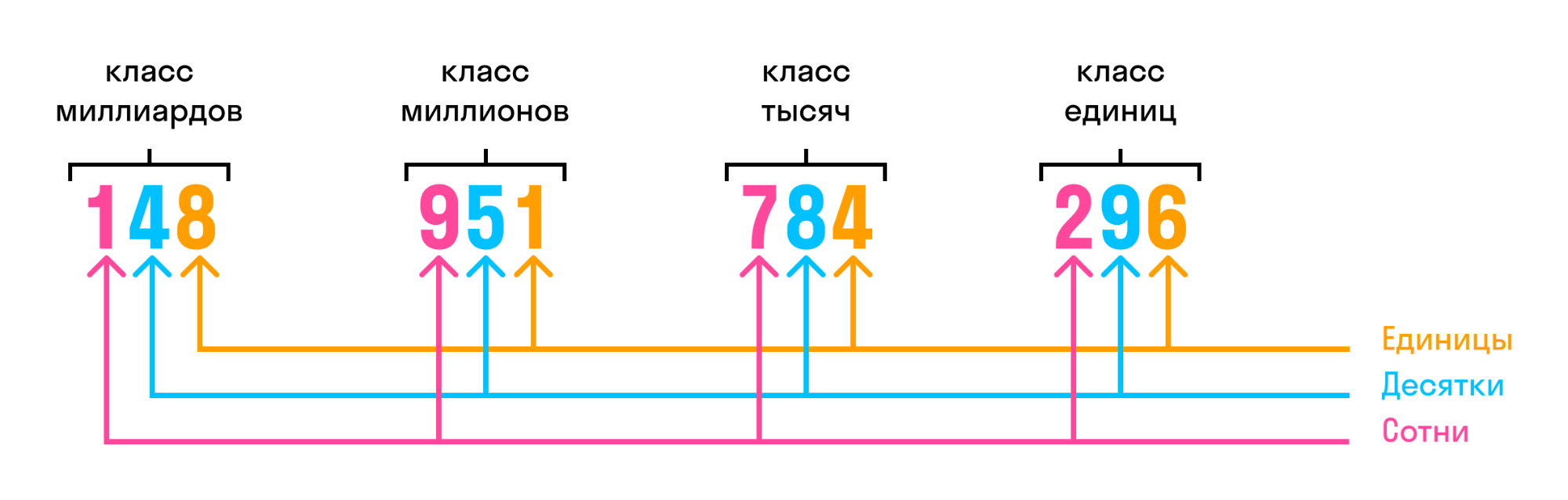
В многозначном числе цифры справа налево разбиваются на группы по три цифры. Такие группы называют классами.

Названия классов многозначных чисел:

• первый — класс единиц,
• второй — класс тысяч,
• третий — класс миллионов,
• четвёртый — класс миллиардов,
• пятый — класс триллионов,
• шестой — класс квадриллионов,
• седьмой — класс квинтиллионов,
• восьмой — класс секстиллионов.

Чтобы чтение многозначного числа не превращалось в головоломку, при записи лучше разграничивать число по классам. Вот так:

• 345 466 129 350 вместо 345466129350

Читаться такое число будет слева направо: триста сорок пять миллиардов четыреста шестьдесят шесть миллионов сто двадцать девять тысяч триста пятьдесят.

Разряд — это место, которое занимает цифра в записи многозначного числа.

Разряды считаются справа налево. Первая цифра справа в записи числа относится к первому разряду.

• Например, в числе 128 656 374 252 разряды считаются справа налево: 2 — первый разряд; 5 — второй разряд; 2 — третий разряд; 4 — четвертый разряд; 7 — пятый разряд; 3 — шестой разряд; 6 — седьмой разряд; 5 — восьмой разряд; 6 — девятый разряд; 8 — десятый разряд; 2 — одиннадцатый разряд; 1 — двенадцатый разряд.

Разрядные единицы — это единицы, десятки, сотни, тысячи, миллионы.

Все разрядные единицы, за исключением простых единиц, — составные единицы. Каждые десять единиц одного разряда составляют одну единицу следующего разряда.

• 10 единиц = 1 десяток;
• 10 десятков = 1 сотня;
• 10 сотен = 1 тысяча;
• 10 тысяч = 1 десяток тысяч;
• 10 десятков тысяч = 1 сотня тысяч;
• 10 сотен тысяч = 1 миллион.

Если составная единица больше другой единицы — она называется единицей высшего разряда. Если меньше, то единицей низшего разряда. Так, например, сотня — единица высшего разряда относительно десятка, но низшего разряда относительно тысячи.

Чтобы выяснить сколько всего в числе единиц определенного разряда, нужно мысленно вычеркнуть из числа все цифры низшего разряда.

• Например, нужно сказать, сколько сотен в числе 5689.

Это значит, нужно выяснить, сколько сотен заключается в тысячах и в сотнях этого числа. 5689 — на третьем месте в классе единиц стоит цифра 6, значит в числе есть 6 сотен. Следующая влево цифра — 5 (тысячи). 1 тысяча = 10 сотен. 5 тысяч = 50 сотен. Всего в числе 56 сотен.

Если в разряде стоит цифра 0, то это означает отсутствие единиц, десятков, сотен и т.д., в зависимости от того, где именно содержится цифра.

Иногда бывает необходимо не только разложить число на разрядные слагаемые, но и определить количество единиц какого-то определенного разряда.

В такой ситуации можете выполнить подробный разбор числа.

• Разберем число 6 057 386

Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть

6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.

Из чего состоит это число? Из:

• шести единиц миллионов (6 * 1 000 000);
• пяти десятков тысяч (5 * 10 000);
• семи единиц тысяч (7 * 1000);
• трех сотен (3 * 100);
• восьми десятков (8 * 10);
• шести единиц (6).

Для того, чтобы алгоритм разложения числа на простые слагаемые был всегда под рукой, сохраняйте себе табличку с примером. В ней вы найдете вопросы, которые помогут разложите любое число.

Определите, сколько единиц в числе 5 068 252.

1. Определяем сколько всего единиц в числе.

2. Определяем количество десятков.
Записываем число без первого разряда (единицы).

3. Определяем количество сотен.
Записываем число без первого
и второго разрядов (десятки и сотни).

4. Определяем количество единиц тысяч.
Записываем число без первого, второго,
третьего разрядов (единицы, десятки, сотни).

5. Определяем количество десятков тысяч.
Записываем число без первого, второго, третьего,
четвертого разрядов (единицы, десятки, сотни, единицы тысяч).

6. Определяем количество сотен тысяч.
Записываем число без десятков тысяч, единиц тысяч,
сотен и единиц.

7. Определяем количество единиц миллионов.
Записываем число без сотен тысяч, десятков тысяч,
единиц тысяч, сотен, десятков, единиц.

Расписав таким образом число, мы выяснили, что в числе 5 068 252: 5 единиц класса миллионов (3 класс); 68 единиц класса тысяч (2 класс); 252 единицы класса единиц (1 класс).

Может показаться, что такой подробный разбор ни к чему, что и без того все понятно, но многоразрядные многозначные числа — коварны. Лучше хорошенько потренироваться, используя все вспомогательные материалы, как эта табличка, а потом уже раскладывать любое число за секунды и в уме.

Примеры

Внимательно просмотрите примеры и попробуйте самостоятельно представить числа в виде суммы разрядных слагаемых.

Представьте в виде суммы разрядных слагаемых:

1. 84 610
   84 610 = 8 * 10 000 + 4 * 1 000 + 6 * 100 + 10
   84 610 = 80 000 + 4 000 + 600 + 10.
2. 45 317
   45 317 = 4 * 10 000 + 5 * 1000 + 3 * 100 + 17
   45 317 = 40 000 + 5 000 + 300 + 17.
3. 56 789
   56 789 = 5 * 10 000 + 6 * 1000 + 7 * 100 + 8 * 10 + 9
   56 789 = 50 000 + 6 000 + 700 + 80 + 9.
4. 345 677
   345 677 = 3 * 100 000 + 4 * 10 000 + 5 * 1000 + 6 * 100 + 7 * 10 + 7
   345 677 = 300 000 + 40 000 + 5 000 + 600 + 70 + 7.
5. 687 543
   687 543 = 6 * 100 000 + 8 * 10 000 + 7 * 1000 + 5 * 100 + 4 * 10 + 3
   687 543 = 600 000 + 80 000 + 7 000 + 500 + 40 + 3.
6. 877 589
   877 589 = 8 * 100 000 + 7 * 10 000 + 7 * 1000 + 5 * 10 + 8 * 10 + 9
   877 589 = 800 000 + 70 000 + 7 000 + 500 + 80 + 9.

Как видите, все довольно просто. Занятие весьма успокаивающее, медитативное. Приятно сесть после тяжелого дня и пораскладывать числа на разрядные слагаемые.

Если вдруг так вышло, что вы не расслабляетесь при виде цифр, то воспользуйтесь онлайн-калькулятором. В интернете таких калькуляторов немало, вот один из них.

1. 4 895 634
   4 895 634 = 4 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 5 * 1000 + 6 * 100 + 3 * 10 + 4
   4 895 634 = 4 000 000 + 800 000 + 90 000 + 5 000 + 600 + 30 +4.
2. 8 675 349
   8 675 349 = 8 * 1 000 000 + 6 * 100 000 + 7 * 10 000 + 5 * 1000 + 3 * 100 + 4 * 10 + 9
   8 675 349 = 8 000 000 + 600 000 + 70 000 + 5 000 + 300 + 40 + 9.
3. 77 897 125
   77 897 125 = 7 * 10 000 000 + 7 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 7 * 1000 + 1 * 100 + 2 * 10 + 5
   77 897 125 = 70 000 000 + 7 000 000 + 800 000 + 90 000 + 7 000 + 100 + 20 + 5.
4. 656 734 212
   656 734 212 = 6 * 100 000 000 + 5 * 10 000 000 + 6 * 1 000 000 + 7 * 100 000 + 3 * 10 000 + 4 * 1000 + 2 * 100 + 1 * 10 + 2
   656 734 212 = 600 000 000 + 50 000 000 + 6 000 000 + 700 000 + 30 000 + 4 000 + 200 + 10 + 2.

Так вы сможете разложить на разрядные слагаемые любое, даже самое гигантское, число. Важно разобраться в разрядах и классах чисел, тогда вы точно ничего не перепутаете.

Источник