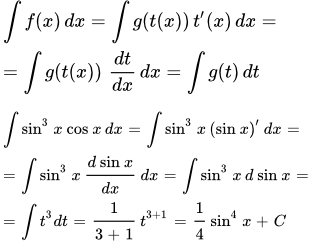Замена переменной или способ подстановки

Лекция 2. Замена переменной и и интегрирование по частям в неопределенном интеграле

Сайт:	Навчальний сайт ХНАДУ
Курс:	Вища Математика (2 семестр) Вишневецький А.Л.
Книга:	Лекция 2. Замена переменной и и интегрирование по частям в неопределенном интеграле

Надруковано:	Гість
Дата:	п’ятниця 19 листопад 2021 23:48

Зміст

Тема 1. Неопределенный интеграл, его свойства

1. Первообразная

Пусть f ( x ) – данная функция.

Определение . Функция F ( x ) называется первообразной для f ( x ) , если

Примеры . x 2 – первообразная для 2 x , т.к. ( x 2 )’ = 2 x . Впрочем, x 2 + 1 и x 2 — 5 – тоже первообразные для 2 x , т.к. ( x 2 + 1)’ = 2 x и ( x 2 — 5)’ = 2 x .

Теорема 1. Если F ( x ) – первообразная для f ( x ) , то

1) F ( x ) + С – тоже первообразная для f ( x ) .

2) Любая первообразная для f ( x ) имеет вид F ( x ) + С для некоторого С.

2. Неопределенный интеграл

Определение . Множество всех первообразных функции f ( x ) называется неопределенным интегралом от этой функции и обозначается так:

Здесь f ( x) dx – подынтегральное выражение, f ( x ) – подынтегральная функция, x – переменная интегрирования.

Если функция непрерывна на некотором отрезке, то на этом отрезке существует её неопределенный интеграл.

Операции нахождения дифференциала и неопределенного интеграла – взаимно обратные:

3. Свойства неопределенного интеграла

Формул «интеграл от произведения» и «интеграл от частного» функций нет.

4. Таблица первообразных

Таблица проверяется с помощью (1). Формулы № 10, 12, 14 есть обобщение формул № 9, 11, 13. В формулах № 10, 12, 14, 15 a ≠ 0 .

Полная запись формулы №1:

Тема 2. Основные методы интегрирования

5. Интегрирование подстановкой (заменой переменной)

Суть метода: путем введения новой переменной интегрирования (т.е. подста­новки) свести данный интеграл к более простому (желательно – к табличному).

Начнем с формулы замены. Надо найти интеграл

Сделаем подстановку φ(t) = x , где φ(t) — функция, имеющая непрерывную производную. По определению дифференциала, dx = φ'(t)dt . Подставляем в (1):

– формула замены переменной в неопределенном интеграле. После ее примене­ния и вычисления полученного интеграла нужно вернуться к исходной перемен­ной. Формулу (2) применяют как «слева направо», так и «справа налево». Общих методов подбора подстановок не существует.

6. Интегрирование по частям

Теорема . Если функции u = u(x) , ν = ν (x) имеют непрерывные производные, то

Док-во . Интегрируя равенство d(uv) = udv + vdu , получим uv = ∫ udv — ∫ vdu , т.е. (5)

Формула (5) сводит нахождение ∫ udv к нахождению ∫ vdu , поэтому ее приме­няют тогда, когда последний интеграл не сложнее первого. Для применения этой формулы подынтегральное выражение представляют как произведение двух сомножителей, один из которых обозначают u , другой dv . Затем u дифференцируют (находят du ), а dv интегрируют (находят v ).

Укажем способ выбора u и dv в двух типичных случаях. Пусть P(x) – многочлен.

Формулу (5) можно применять повторно. Например, в случае а) это делают n раз, где n – степень многочлена P(x) .

7. Интегрирование простейших рациональных дробей

Простейшие рациональные дроби – это дроби:

1 рода: ( k N ) и 2 рода: (дискриминант знаменателя D n = 1 так:

• Заменить

• Разложить интеграл в сумму вида

К первому интегралу применить формулу (4), а второй – табличный (арктангенс).

Источник

Интегрирование методом замены переменной

Метод замены переменной

С помощью замены переменной можно вычислить простые интегралы и, в некоторых случаях, упростить вычисление более сложных.

Метод замены переменной заключается в том, что мы от исходной переменной интегрирования, пусть это будет x , переходим к другой переменной, которую обозначим как t . При этом мы считаем, что переменные x и t связаны некоторым соотношением x = x ( t ) , или t = t ( x ) . Например, x = ln t , x = sin t , t = 2 x + 1 , и т.п. Нашей задачей является подобрать такую зависимость между x и t , чтобы исходный интеграл либо свелся к табличному, либо стал более простым.

Основная формула замены переменной

Рассмотрим выражение, которое стоит под знаком интеграла. Оно состоит из произведения подынтегральной функции, которую мы обозначим как f ( x ) и дифференциала dx : . Пусть мы переходим к новой переменной t , выбрав некоторое соотношение x = x ( t ) . Тогда мы должны выразить функцию f ( x ) и дифференциал dx через переменную t .

Чтобы выразить подынтегральную функцию f ( x ) через переменную t , нужно просто подставить вместо переменной x выбранное соотношение x = x ( t ) .

Преобразование дифференциала выполняется так:
.
То есть дифференциал dx равен произведению производной x по t на дифференциал dt .

На практике, чаще всего встречается случай, в котором мы выполняем замену, выбирая новую переменную как функцию от старой: t = t ( x ) . Если мы догадались, что подынтегральную функцию можно представить в виде
,
где t′ ( x ) – это производная t по x , то
.

Итак, основную формулу замены переменной можно представить в двух видах.
(1) ,
где x – это функция от t .
(2) ,
где t – это функция от x .

Важное замечание

В таблицах интегралов переменная интегрирования, чаще всего, обозначается как x . Однако стоит учесть, что переменная интегрирования может обозначаться любой буквой. И более того, в качестве переменной интегрирования может быть какое-либо выражение.

В качестве примера рассмотрим табличный интеграл
.

Здесь x можно заменить любой другой переменной или функцией от переменной. Вот примеры возможных вариантов:
;
;
.

В последнем примере нужно учитывать, что при переходе к переменной интегрирования x , дифференциал преобразуется следующим образом:
.
Тогда
.

В этом примере заключена суть интегрирования подстановкой. То есть мы должны догадаться, что
.
После чего интеграл сводится к табличному.
.

Можно вычислить этот интеграл с помощью замены переменной, применяя формулу (2). Положим t = x 2 + x . Тогда
;
;

.

Примеры интегрирования заменой переменной

1) Вычислим интеграл
.
Замечаем, что (sin x )′ = cos x . Тогда

.
Здесь мы применили подстановку t = sin x .

2) Вычислим интеграл
.
Замечаем, что . Тогда

.
Здесь мы выполнили интегрирование заменой переменной t = arctg x .

3) Проинтегрируем
.
Замечаем, что . Тогда

. Здесь, при интегрировании, произведена замена переменной t = x 2 + 1 .

Линейные подстановки

Пожалуй, самыми распространенными являются линейные подстановки. Это замена переменной вида
t = ax + b ,
где a и b – постоянные. При такой замене дифференциалы связаны соотношением
.

Примеры интегрирования линейными подстановками

B) Найти интеграл
.
Решение.
Воспользуемся свойствами показательной функции.
.
ln 2 – это постоянная. Вычисляем интеграл.

.

C) Вычислить интеграл
.
Решение.
Приведем квадратный многочлен в знаменателе дроби к сумме квадратов.
.
Вычисляем интеграл.

.

D) Найти интеграл
.
Решение.
Преобразуем многочлен под корнем.

.
Интегрируем, применяя метод замены переменной .

.
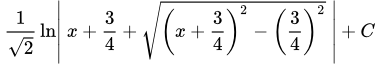
Ранее мы получили формулу
.
Отсюда
.
Подставив это выражение, получим окончательный ответ.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 06-09-2015

Источник

Замена переменных в уравнениях (ЕГЭ 2022)

Метод замены переменных… Что это за зверь?

Это хитрый способ сначала сделать сложное уравнение простым (с помощью замены переменных) и потом быстро с ним разделаться.

Есть три способа замены переменной.

Читай эту статью — ты все поймешь!

Замена переменных — коротко о главном

Определение:

Замена переменных – метод решения сложных уравнений и неравенств, который позволяет упростить исходное выражение и привести его к стандартному виду.

Замена переменных – это введение нового неизвестного, относительно которого уравнение или неравенство имеет более простой вид.

Виды замены переменной:

Степенная замена: за \( \displaystyle t\) принимается какое-то неизвестное, возведенное в степень: \( \displaystyle t=<^>\).

Дробно-рациональная замена: за \( \displaystyle t\) принимается какое-либо отношение, содержащее неизвестную переменную: \( \displaystyle t=\frac<<

_>\left( x \right)><<_>\left( x \right)>\), где \( \displaystyle <

_>\left( x \right)\) и \( \displaystyle <_>\left( x \right)

\) – многочлены степеней n и m, соответственно.

Замена многочлена: за \( \displaystyle t\) принимается целое выражение, содержащее неизвестное: \( \displaystyle t=<

_>\left( x \right)\) или \( \displaystyle t=\sqrt<<

_>\left( x \right)>\), где \( \displaystyle <

_>\left( x \right)

\) – многочлен степени \( \displaystyle n\).

Обратная замена:

После решения упрощенного уравнения/неравенства, необходимо произвести обратную замену.

Степенная замена \( \displaystyle y=<^>\)

Решение примера №1

Допустим, у нас есть выражение: \( \displaystyle <^<4>>-5<^<2>>-36=0\).

Подумай, к какому виду мы можем его привести, чтобы при расчетах легко найти корни? Правильно, данное уравнение необходимо привести к квадратному виду.

Введем новую переменную \( \displaystyle t=<^<2>>\).

Метод замены переменной подразумевает, чтобы старой переменной \( \displaystyle x\) не оставалось – в выражении должна остаться только одна переменная – \( \displaystyle t\).

Наше выражение приобретет вид:

\( \displaystyle <^<2>>-5t-36=0\) – обычное квадратное уравнение

\( \displaystyle \text=<<\text>^<2>>-4\text\) \( \displaystyle \text=25-4\cdot 1\cdot \left( -36 \right)=25+144=169\) \( \displaystyle \sqrt<\text>=\sqrt<169>=13\) \( \displaystyle <_<1,2>>=\frac<-b\pm \sqrt><2a>\) \( \displaystyle <_<1>>=\frac<5+13><2>=9\) \( \displaystyle <_<2>>=\frac<5-13><2>=-4\)

Нашли ли мы корни исходного уравнения? Правильно, нет.

На этом шаге не следует забывать, что нам необходимо найти значения переменной \( \displaystyle x\), а мы нашли только \( \displaystyle t\).

Следовательно, нам необходимо вернуться к исходному выражению, то есть сделать обратную замену — вместо \( \displaystyle t\) ставим \( \displaystyle <^<2>>\).

Решаем два новых простых уравнения, не забывая область допустимых значений!

При \( \displaystyle <^<2>>=9\) у нас будет два корня:

\( \displaystyle <_<1>>=3\) \( \displaystyle <_<2>>=-3\)

А что у нас будет при \( \displaystyle <^<2>>=-4\)?

Правильно. Решений данного уравнения нет, так как квадрат любого числа – число положительное, а в нашем случае – отрицательное, соответственно, при \( \displaystyle <^<2>>=-4\) у нас будет пустое множество (решения нет).

В ответ следует записать необходимые нам корни, то есть \( \displaystyle x\), которые существуют:

Ответ: \( \displaystyle 3\);\( \displaystyle -3\)

Точно таким же образом необходимо действовать при решении неравенств.

Выполняя замену переменных, необходимо помнить два простых правила:

• Замену переменных нужно делать сразу и при первой же возможности.
• Уравнение (неравенство) относительно новой переменной необходимо решать до конца, и лишь затем возвращаться к старому неизвестному.
• При возврате к изначальному неизвестному (да и вообще на протяжении всего решения), не забывай проверять корни на ОДЗ.

Решение примера №2

Попробуй самостоятельно применить метод замены переменной в уравнении \( \displaystyle 3<^<6>>-7<^<3>>+2=0\).

Подумай, к какому виду мы можем его привести, чтобы при расчетах легко найти корни?

Проверь свое решение:

Введем новую переменную \( \displaystyle t=<^<3>>\).

Наше выражение приобретет вид:

\( \displaystyle 3<^<2>>-7t+2=0\) – обычное квадратное уравнение

Возвращаемся к исходному выражению, то есть делаем обратную замену: вместо \( \displaystyle t\) ставим \( \displaystyle <^<3>>\)

Оба значения \( \displaystyle <^<3>>\) имеют право на существование. Решаем два получившихся уравнения:

При \( \displaystyle <^<3>>=2\Rightarrow x=\sqrt[3]<2>\)

Ответ: \( \displaystyle \sqrt[3]<2>;\sqrt[3]<\frac<1><3>>\)

Степенная замена в общем виде

Например, с помощью замены \( \displaystyle t=<^<2>>\) биквадратное уравнение \( \displaystyle a<^<4>>+b<^<2>>+c=0,\text< >a\ne 0\) приводится к квадратному: \( \displaystyle a<^<2>>+bt+c=0\).

В неравенствах все аналогично.

Например, в неравенстве \( \displaystyle a<^<6>>+b<^<3>>+c\ge \text<0>\) сделаем замену \( \displaystyle t=<^<3>>\), и получим квадратное неравенство: \( \displaystyle a<^<2>>+bt+c\ge \text<0>\).

Дробно-рациональная замена

Дробно-рациональная замена – \( \displaystyle y=\frac<<

_>\left( x \right)><<_>\left( x \right)>,

\) многочлены степеней n и m соответственно.

При этом необходимо помнить, что область допустимых значений (ОДЗ) данного уравнения \( \displaystyle <_>\left( x \right)\ne 0\) (так как на ноль делить нельзя).

Решение примера №3

Допустим, у нас есть уравнение:

Так как на ноль делить нельзя, то в данном случае ОДЗ будет: \( \displaystyle x\ne 0\)

Введем новую переменную \( \displaystyle t\).

Пусть \( \displaystyle t=x+\frac<3>\), тогда

Сравни, что дает возведение \( \displaystyle t\) в квадрат, с первой сгруппированной скобкой в нашем примере. Что ты видишь?

Правильно. Разница между тем, что у нас в примере, и тем, что дает нам возведение в квадрат, заключается в удвоенном произведении слагаемых.

Соответственно, его и следует вычесть, переписывая наш пример с переменной \( \displaystyle t\).

\( \displaystyle 2\cdot \frac<3><>=6\)

В итоге мы получаем следующее выражение:

\( \displaystyle <^<2>>-6-t-14=0\) – обычное квадратное уравнение.

Решаем получившееся уравнение:

Как мы помним \( t\), не является конечным решением уравнения. Возвращаемся к изначальной переменной:

Приводя к общему знаменателю \( \displaystyle x\), мы приходим к совокупности 2-x квадратных уравнений:

Решим первое квадратное уравнение:

На этой стадии не забываем про ОДЗ.

Мы должны посмотреть, удовлетворяют ли найденные корни области допустимых значений? Если какой-то корень не удовлетворяет ОДЗ – он не включается в конечное решение уравнения.

Решим второе квадратное уравнение:

Снова смотрим, удовлетворяют ли полученные корни ОДЗ? Далее записываем конечный ответ.

Ответ: \( \displaystyle \frac<5+\sqrt<13>><2>;\text< >\!\!

У тебя получился такой же?

Попробуй решить все с начала до конца самостоятельно.

Решение пример №4

Какой ответ у тебя получился? У меня \( \displaystyle 1\) и \( \displaystyle 3\).

Сравним ход решения:

Пусть \( \displaystyle t=\frac<1><<<\left( -2 \right)>^<2>>>\), тогда выражение приобретает вид:

Приведем слагаемые к общему знаменателю:

Не забываем про ОДЗ — \( \displaystyle t\ne 0\).

Решаем квадратное уравнение:

Как ты помнишь, \( \displaystyle t\) не является конечным решением уравнения. Возвращаемся к изначальной переменной:

Решим первое уравнение:

Решением первого уравнения являются корни \( \displaystyle 1\) и \( \displaystyle 3\).

Решим второе уравнение:

Решения не существует. Подумай, почему? Правильно! \( \displaystyle \frac<1><<<\left( -2 \right)>^<2>>>=-\frac<1><5>\) – число положительное, \( \displaystyle <<\left( -2 \right)>^<2>>\) — тоже всегда положительно, следовательно, при делении положительного числа на положительное никак не может получиться отрицательное!

Ответ: \( \displaystyle 1\); \( \displaystyle 3\)

Дробно-рациональная замена в общем виде

\( \displaystyle <

_>\left( x \right)\) и \( \displaystyle <_>\left( x \right)\) − многочлены степеней \( \displaystyle n\) и \( \displaystyle m\) соответственно.

Например, при решении возвратных уравнений, то есть уравнений вида

обычно используется замена \( \displaystyle t=x+\frac<1>\).

Сейчас покажу, как это работает.

Легко проверить, что \( \displaystyle x=0\) не является корнем этого уравнения: ведь если подставить \( \displaystyle x=0\) в уравнение, получим \( \displaystyle a=0\), что противоречит условию.

Разделим уравнение на \( \displaystyle <^<2>>\ne 0\):

Теперь делаем замену: \( \displaystyle t=x+\frac<1>\).

Прелесть ее в том, что при возведении в квадрат в удвоенном произведении слагаемых сокращается x:

Вернемся к нашему уравнению:

\( \displaystyle \begina\left( <^<2>>+\frac<1><<^<2>>> \right)+b\left( x+\frac<1> \right)+c=0\text< >\Leftrightarrow \text< >a\left( <^<2>>-2 \right)+bt+c=0\text< >\Leftrightarrow \\a<^<2>>+bt+c-2a=0\end\)

Теперь достаточно решить квадратное уравнение и сделать обратную замену.

Замена многочлена

Замена многочлена \( \displaystyle y=<

_>\left( x \right)\) или \( \displaystyle y=\sqrt<<

_>\left( x \right)>\).

Здесь \( \displaystyle <

_>\left( x \right)

\) — многочлена степени \( \displaystyle n\), например, выражение \( \displaystyle 12<^<3>>+2<^<2>>-3x+1\) – многочлен степени \( \displaystyle 3\).

Решение примера №4

Применим метод замены переменной. Как ты думаешь, что нужно принять за \( \displaystyle t\)?

Уравнение приобретает вид:

Производим обратную замену переменных:

Решим первое уравнение:

Решим второе уравнение:

\( \displaystyle <<>^<2>>-4+8=0\) \( \displaystyle \text=<<>^<2>>-4\) \( \displaystyle \text=16-4\cdot 8=16-32=-16\)

Решил? Теперь проверим с тобой основные моменты.

За \( \displaystyle t\) нужно взять \( \displaystyle 2<<>^<2>>-9+5\).

Мы получаем выражение:

\( \displaystyle \text\cdot \left( \text+1 \right)=2\)

Решая квадратное уравнение, мы получаем, что \( t\) имеет два корня: \( \displaystyle -2\) и \( \displaystyle 1\).

Далее делаем обратную замену и решаем оба квадратных уравнения.

Решением первого квадратного уравнения являются числа \( \displaystyle 1\) и \( \displaystyle 3,5\)

Решением второго квадратного уравнения — числа \( \displaystyle 0,5\) и \( \displaystyle 4\).

Ответ: \( \displaystyle 0,5\); \( \displaystyle 1\); \( \displaystyle 3,5\); \( \displaystyle 4\)

Замена многочлена в общем виде

\( \displaystyle t=<

_>\left( x \right)\) или \( \displaystyle t=\sqrt<<

_>\left( x \right)>\).

Здесь \( \displaystyle <

_>\left( x \right)\) − многочлен степени \( \displaystyle n\), т.е. выражение вида

(например, выражение \( \displaystyle 4<^<4>>+2<^<3>>-3x+1\) – многочлен степени \( \displaystyle 4\), то есть \( \displaystyle <

_<4>>\left( x \right)\)).

Чаще всего используется замена квадратного трехчлена: \( \displaystyle t=a<^<2>>+bx+c\) или \( \displaystyle t=\sqrt^<2>>+bx+c>\).

Подведем итоги

Метод замены переменной имеет \( \displaystyle 3\) основных типа замен переменных в уравнениях и неравенствах:

Степенная замена, когда за \( \displaystyle t\) мы принимаем какое-то неизвестное, возведенное в степень.

Замена многочлена, когда за \( \displaystyle t\) мы принимаем целое выражение, содержащее неизвестное.

Дробно-рациональная замена, когда за \( \displaystyle t\) мы принимаем какое-либо отношение, содержащее неизвестную переменную.

Важные советы при введении новой переменной

• Замену переменных нужно делать сразу и при первой же возможности.
• Уравнение (неравенство) относительно новой переменной необходимо решать до конца, и лишь затем возвращаться к старому неизвестному.
• При возврате к изначальному неизвестному (да и вообще на протяжении всего решения), не забывай проверять корни на ОДЗ.
• Новая переменная вводится аналогичным образом, как в уравнениях, так и в неравенствах.

Разбор 3 примеров на замену переменных

Пример 7. \( \displaystyle \left( <<>^<2>>-4+7 \right)\left( <<>^<2>>-4+6 \right)=12\)

Решение примера №6

Пусть \( \displaystyle \text=<<>^<3>>\), тогда выражение приобретает вид \( \displaystyle <^<2>>+7\text-8=0\).

Так как \( \displaystyle \text=<<>^<3>>\), то может быть как положительным, так и отрицательным.

Ответ: \( \displaystyle -2;\text< >1\)

Решение примера №7

Пусть \( \displaystyle \text=<<>^<2>>-4+7\), тогда выражение приобретает вид \( \displaystyle \text\cdot \left( \text-1 \right)=12\).

\( \displaystyle <<\text>_<2>>=-3\Rightarrow \) решения нет, так как \( \displaystyle D

Решение:

Это дробно-рациональное уравнение (повтори «Рациональные уравнения»), но решать его обычным методом (приведение к общему знаменателю) неудобно, так как мы получим уравнение \( \displaystyle 6\) степени, поэтому применяется замена переменных.

Все станет намного проще после замены: \( \displaystyle t=<^<3>>\). Тогда \( \displaystyle <^<6>>=<^<2>>\):

Теперь делаем обратную замену:

Ответ: \( \displaystyle \sqrt[3]<3>\); \( \displaystyle \sqrt[3]<4>\).

Решение примера 10 (замена многочлена)

Решите уравнение \( \displaystyle \left( <^<2>>+5x+9 \right)\left( <^<2>>+5x+10 \right)=12\).

Решение:

И опять используется замена переменных \( \displaystyle t=<^<2>>+5x+9\). Тогда уравнение примет вид:

\( \displaystyle t\cdot \left( t+1 \right)=12\text< >\Rightarrow \text< ><^<2>>+t-12=0\).

Корни этого квадратного уравнения: \( \displaystyle t=-4\) и \( \displaystyle t=3\). Имеем два случая. Сделаем обратную замену для каждого из них:

\( \displaystyle t=-4\text< >\Rightarrow \text< ><^<2>>+5x+9=-4\text< >\Rightarrow \text< ><^<2>>+5x+13=0\);

\( \displaystyle D=<<5>^<2>>-4\cdot 13=-17

\( \displaystyle x\in \left[ -\frac<7><2>;-\frac<1> <2>\right]\cup \left( 0;+\infty \right)\)

\( \displaystyle y 0\) при всех \( \displaystyle x\), так как \( \displaystyle D=64-4\cdot 4\cdot 7=-48 0\) при всех \( \displaystyle x\), так как \( \displaystyle D=81-4\cdot 4\cdot 7=-31 0\)

Источник

Читайте также:  Способы уплаты ндфл индивидуальными предпринимателями