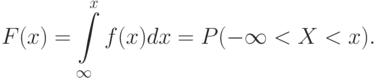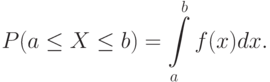Закон распределения вероятностей способы задания
Случайной называется величина, которая в результате испытания может принять то или иное числовое значение, причем заранее неизвестно, какое именно.
Если для какой- либо величины ее измерение повторять многократно в практически одинаковых условиях, то обнаружится, что всякий раз получаются несколько отличные друг от друга результаты. Это складывается влияние причин двух видов: 1) основных, определяющих главное значение результата; 2) второстепенных, обуславливающих их расхождение.
При совместном действии этих причин понятия необходимости и случайности оказываются тесно связанными между собой, но необходимое преобладает над случайным.
Таким образом, возможные значения случайных величин принадлежат некоторым числовым множествам.
Случайным является то, что на этих множествах величины могут принять любое значение, но какое именно, заранее сказать нельзя.
Случайная величина связана со случайным событием.
Если случайное событие — качественная характеристика испытаний, то случайная величина — его количественная характеристика.
Законы распределения могут быть заданы тремя способами: табличным, графическим, аналитическим. Способ задания зависит от типа случайной величины.
Различают два основных типа случайных величин: дискретные и непрерывно распределенные случайные величины.
Источник
СПОСОБЫ ЗАДАНИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН



НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Методические указания к практическим занятиям
по дисциплине «Высшая математика»
Составители: Ю.Б. Егорова
МОСКВА2009
Егорова Ю.Б., Мамонов И.М. Непрерывные случайные величины:Методические указания к практическим занятиямпо дисциплине «Высшая математика»/ Ю.Б. Егорова, И.М. Мамонов. М.: МАТИ, 2009. 12 с.
ВВЕДЕНИЕ
Методические указания предназначены для студентов дневного и вечернего отделения факультета №14 специальностей 150601, 160301, 220301, 230102. Методические указания служат основой для практических занятий и выполнения индивидуальных заданий.
СПОСОБЫ ЗАДАНИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
1.1. Непрерывная случайная величина– величина, которая может принимать любое значение из некоторого промежутка числовой оси (конечного или бесконечного). Примеры непрерывных случайных величин: дальность полета артиллерийского снаряда, расход электроэнергии за определенный промежуток времени, температура тела или воздуха, вес изделия, рост человека и т.п.
1.2. Закон распределениянепрерывной случайной величины можно задать двумя аналитическими способами:
1) с помощью функции распределения вероятностей F(x);
2) с помощью плотности распределения вероятностей f(х).
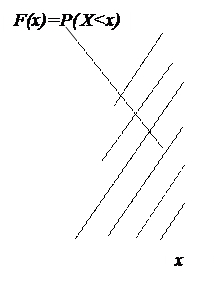
1.3.Функцией распределения непрерывной случайной величины называют функцию F(x), определяющую для каждого значения х вероятность того, что случайная величина Х примет значение, меньшее заданного х, т.е. F(x)=P(X
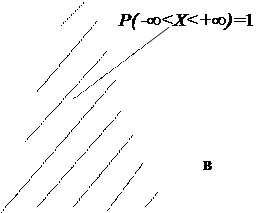
3. Вероятность попадания непрерывной случайной величины Х в интервал от -µдо +Ґравна 1:
С геометрической точки зрения это означает, что вся площадь под кривой распределения = 1 (см. рис. 1, в).
4. Интегральную функцию распределения F(x) непрерывной случайной величины можно выразить через плотность распределения вероятностей по формуле:
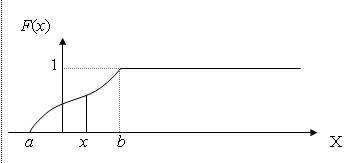
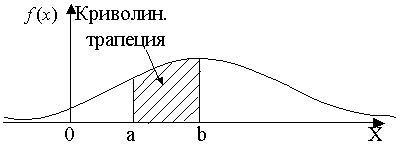
С геометрической точки зрения интегральная функция распределения равна площади заштрихованной фигуры, ограниченной сверху кривой распределения и лежащей левее точки х (рис. 1, г).
| |
 | |
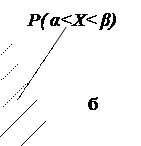 | |
| |
 | |
 |  |
| |
|
1.5. Свойства непрерывных случайных величин:
1. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю:
2. Вероятность попадания непрерывной случайной величины Х в интервал от (α, β) не зависит от того, является ли этот интервал открытым или закрытым:
Источник
Закон распределения вероятностей способы задания
1. Формирование представление о случайной величине, дискретных и непрерывных случайных величинах.
2. Знакомство с законом распределения дискретной случайной величины, функцией распределения и плотностью распределения непрерывной случайной величины, числовых характеристиках случайных величин.
1. Виды случайных величин.
2. Закон распределения дискретной случайной величины.
3. Функция распределения вероятностей случайной величины.
4. Плотность распределения вероятностей непрерывной случайной величины.
5. Математическое ожидание.
6. Дисперсия и среднеквадратическое отклонение.
1. Виды случайных величин.
Случайной величиной называется такая величина, которая случайно принимает какое-то значение из множества возможных значений.
Случайные величины обозначаются: X , Y , Z . Значения, которые они принимают: x , y , z .
По множеству возможных значений различают дискретные и непрерывные случайные величины.
Дискретными называются случайные величины, значениями которых являются только отдельные точки числовой оси. (Число их может быть как конечно, так и бесконечно).
Пример: Число родившихся девочек среди ста новорожденных за последний месяц- это дискретная случайная величина, которая может принимать значения 1,2,3,…
Непрерывными называются случайные величины, которые могут принимать все значения из некоторого числового промежутка.
Пример: Расстояние, которое пролетит снаряд при выстреле- это непрерывная случайная величина, значения которой принадлежат некоторому промежутку [а; в].
2. Закон распределения дискретной случайной величины.
Дискретную случайную величину Х можно характеризовать законом распределения .
Закон распределения дискретной случайной величины— это соответствие между возможными значениями случайной величины и их вероятностями.
Закон распределения можно задать таблично, аналитически, графически.
При задании закона распределения таблично, в первую строку таблицы вносятся возможные значения случайно величины, а во вторую- их вероятности.
Пример: Монету подбросили 3 раза. Запишите закон распределения числа выпадения «герба».
Возможные значения данной случайной величины: 0, 1, 2, 3.
Найдем вероятность того, что «герб» не появится (0 раз).
Найдем вероятность того, что «герб» появится 1 раз.
Найдем вероятность того, что «герб» появится 2 раза.
Найдем вероятность того, что «герб» появится 3 раза.
Тогда закон распределения данной дискретной случайной величины можно представить таблицей:
Для наглядности закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки с координатами (xi ; pi), а затем соединяют их отрезками прямых. Полученная фигура называется многоугольником распределения.
Однако, такой способ задания (перечисление всех возможных значений случайной величины и их вероятностей) не подходит для непрерывных случайных величин. Составить перечень их возможных значений невозможно.
3. Функция распределения вероятностей случайной величины.
Дадим новый способ задания любых типов случайных величин. С этой целью введем функцию распределения вероятностей случайной величины.
Функцией распределения случайной величины называют функцию F ( x ), определяющую вероятность того, что случайная величина Х в результате испытания примет значение меньшее х, т.е. F ( x ) P ( X x ).
Геометрически это равенство можно истолковать так: F ( x ) –есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Иногда вместо термина «функция распределения» используется термин «интегральная функция».
Свойства функции распределения:
Свойство 1: Значения функции распределения принадлежат интервалу [0; 1]: .
Свойство 2: F ( x )- неубывающая функция, т.е. при .
Следствие 1: Вероятность того, что случайная величина примет значение, заключенное в интервале (а; b ), равна приращению функции распределения на этом интервале:
Пример: Случайная величина Х задана функцией распределения:
Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0; 2).
Свойство 3: Если возможные значения случайной величины принадлежат интервалу ( a ; b ), то F ( x )=0 при (т.к. ; F ( x )=1 при (т.к. — достоверное событие.
Следствие: Если возможные значения непрерывной случайной величины распределены на всей числовой оси, то справедливы следующие предельные соотношения:
Рассмотренные выше свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.
График расположен в полосе, ограниченной прямыми у=0, у=1 (1 свойство).
4. При возрастании значения х в интервале ( a ; b ), в котором заключены все возможные значения случайной величины, график растет вверх (2 свойство).
5. При ординаты графика равны 0, при ординаты графика равны 1 (3 свойство).
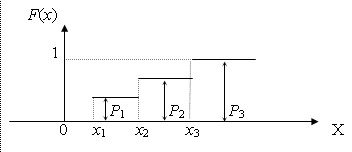
Замечание: График функции распределения дискретной случайной величины имеет ступенчатый вид.
Пример: Дискретная случайная величина Х задана таблицей распределения:
Найдите функцию распределения и постройте ее график.
Решение: Если , то F ( x )=0 по 3 свойству. Если , то F ( x )= P ( X Если , то F ( x )= P ( X Если х>8, то F ( x )=1. Действительно, событие Х
Итак, функция распределения имеет следующий вид:
4. Плотность распределения вероятностей непрерывной случайной величины.
Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (дифференциальной функцией).
Плотность распределения вероятностей непрерывной случайной величины Х называют функцию f ( x )- первую производную от функции распределения F ( x ).
Теорема: Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу ( a ; b ), равна определенному интегралу от плотности распределения, взятому в пределах от а до b .
Пример: Задана плотность вероятностей случайной величины Х.
Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).
Свойства плотности распределения вероятностей:
Свойство 1: Плотность распределения- неотрицательная функция: f ( x ) > 0.
Свойство 2: Несобственный интеграл от плотности распределения в пределах от равен 1: .
Геометрический смысл этого свойства заключается в следующем: площадь криволинейной трапеции, ограниченной осью ОХ и кривой распределения, равна 1. В частности, если все возможные значения случайной величины принадлежат интервалу ( a ; b ), то .
Часто, для того чтобы характеризовать случайную величину используют числа, которые описывают случайную величину суммарно. Такие числа называются числовыми характеристиками случайной величины. К числу важнейших числовых характеристик относятся математическое ожидание и дисперсия.
5. Математическое ожидание.
Математическое ожидание приближенно равно среднему значению случайной величины. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и следовательно стреляет лучше.
Математическое ожидание дискретной случайной величины Х- это величина , где xi— значения случайной величины, pi— их вероятности, n — число возможных значений случайной величины.
Пример: Найдите математическое ожидание, зная закон распределения дискретной случайной величины.
Источник
Случайные события, случайные величины. Их законы распределения и числовые характеристики
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение , наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Обозначим: X, Y, Z – случайные величины
xi, yi, zi – возможные значения случайных величин.
Дискретной (прерывной) называют случайную величину, которая принимает отдельные возможные значения 
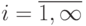
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины, независимо от величины промежутка, бесконечно
Для задания дискретной случайной величины недостаточно перечислить все ее возможные значения, нужно указать еще и их вероятность .
Законом распределения дискретной случайной величины называют соответствие между ее возможными значениями и вероятностями их появления. Закон распределения можно задать таблично, аналитически (в виде формулы) и графически (в виде многоугольника распределения).
Табличное задание закона распределения:
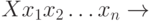

Аналитическое задание закона распределения:
Биномиальное распределение , определяемое распределением Бернулли
k = 0, 1, 2, …, n – количество возможных появлений событий
q = 1-p – вероятность не появления событий.
Распределение Пуассона , определяемое асимптотической формулой Пуассона:

Графическое задание закона распределения представлено на рис.6.1.
Способ описания распределения случайной величины в виде таблицы, в виде формулы или графически применим только для дискретных случайных величин .
Интегральная функция распределения позволяет задать как дискретную, так и непрерывную случайную величину.
Интегральная функция распределения (ИФР)– это функция F(x) , определяющая для каждого возможного значения x вероятность того, что случайная величина X примет значение меньшее x , т. е.
Геометрический смысл интегральной функции распределения – это вероятность того, что случайная величина X примет значение , которое на числовой оси лежит левее точки x .
Свойства интегральной функции распределения:
- Значения интегральной функции распределения принадлежат отрезку [0;1] :
..
- Вероятность того, что случайная величина X примет значение, заключенной в интервале (a,b) , равна приращению интегральной функции распределения на этом интервале
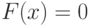
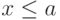


График ИФР непрерывной случайной величины представлен на рис. 6.2
График ИФР дискретной случайной величины представлен на рис. 6.3
Для описания распределения вероятностей непрерывной случайной величины используется дифференциальная функция распределения.
Дифференциальная функция распределения (ДФР) (или плотность вероятности) – это первая производная от интегральной функции.
Интегральная функция распределения является первообразной для дифференциальной функции распределения. Тогда
Вероятность того, что непрерывная случайная величина X примет значение , принадлежащее интервалу (a,b) , равна определенному интегралу от дифференциальной функции, взятому в пределах от a до b :
Геометрический смысл ДФР состоит в следующем: вероятность того, что непрерывная случайная величина X примет значение , принадлежащее интервалу (a, b) , равна площади криволинейной трапеции, ограниченной осью x , кривой распределения f(x) и прямыми x = a и x = b (рис. 6.4).
График дифференциальной функции распределения принято называть кривой распределения.
Источник





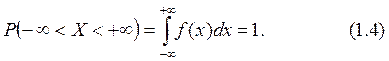




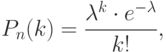

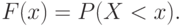
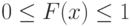 ..
..