Закон распределения случайной величины можно задать следующими способами

Закон распределения дискретной случайной величины. Примеры решения задач

Как известно, случайной величиной называется переменная величина, которая может принимать те или иные значения в зависимости от случая. Случайные величины обозначают заглавными буквами латинского алфавита (X, Y, Z), а их значения – соответствующими строчными буквами (x, y, z). Случайные величины делятся на прерывные (дискретные) и непрерывные.

Дискретной случайной величиной называется случайная величина, принимающая лишь конечное или бесконечное (счетное) множество значений с определенными ненулевыми вероятностями.

Законом распределения дискретной случайной величины называется функция, связывающая значения случайной величины с соответствующими им вероятностями. Закон распределения может быть задан одним из следующих способов.

1. Закон распределения может быть задан таблицей:

Значения xi	x1	x2	x3	.	xn
Вероятности pi	p1	p2	p3	.	pn

События X = x_i (i = 1, 2, 3,…,n) являются несовместными и единственно возможными, т.е. они образуют полную систему событий. Поэтому сумма их вероятностей равна единице: р₁+р₂+р₃+…+р_n = ∑p_i =1

2. Закон распределения может быть задан аналитически (формулой) P(X = x_i) = ϕ(x_i). Например:

а) с помощью биномиального распределения: P_n(X=k) = С_n k p k q n-k , 0 0, k = 0, 1, 2, … .

в) с помощью функции распределения F(x), определяющей для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, т.е. F(x) = P(X 2 или D(X) = M(X 2 )−[M(X)] 2 . Разность X–M(X) называют отклонением случайной величины от ее математического ожидания.
Для биномиального распределения D(X)=npq, для распределения Пуассона D(X)=λ

Среднее квадратическое отклонение (стандартное отклонение) σ(X)=√D(X).

Примеры решения задач по теме «Закон распределения дискретной случайной величины»

Задача 1.

Выпущено 1000 лотерейных билетов: на 5 из них выпадает выигрыш в сумме 500 рублей, на 10 – выигрыш в 100 рублей, на 20 – выигрыш в 50 рублей, на 50 – выигрыш в 10 рублей. Определить закон распределения вероятностей случайной величины X – выигрыша на один билет.

Решение. По условию задачи возможны следующие значения случайной величины X: 0, 10, 50, 100 и 500.

Число билетов без выигрыша равно 1000 – (5+10+20+50) = 915, тогда P(X=0) = 915/1000 = 0,915.

Аналогично находим все другие вероятности: P(X=0) = 50/1000=0,05, P(X=50) = 20/1000=0,02, P(X=100) = 10/1000=0,01, P(X=500) = 5/1000=0,005. Полученный закон представим в виде таблицы:

Значения xi	0	10	50	100	500
Вероятности pi	0,915	0,05	0,02	0,01	0,005

Задача 2.

Найти математическое ожидание числа очков, выпадающих при бросании игральной кости.

Решение. Случайная величина X числа очков принимает значения 1, 2, 3, 4, 5, 6. Вероятность того, что выпадет одно из данных значений равна 1/6. Закон распределения представим в виде таблицы:

Значения xi	1	2	3	4	5	6
Вероятности pi	1/6	1/6	1/6	1/6	1/6	1/6

Найдем математическое ожидание величины Х: М(Х) = 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = (1+2+3+4+5+6)/6 = 21/6 = 3,5

Задача 3.

Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте, построить многоугольник распределения. Найти функцию распределения F(x) и построить ее график. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины.

Решение. 1. Дискретная случайная величина X= <число отказавших элементов в одном опыте>имеет следующие возможные значения: х₁=0 (ни один из элементов устройства не отказал), х₂=1 (отказал один элемент), х₃=2 (отказало два элемента) и х₄=3 (отказали три элемента).

Отказы элементов независимы друг от друга, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, n=3, р=0,1, q=1-р=0,9, определим вероятности значений:
P₃(0) = С₃ 0 p 0 q 3-0 = q 3 = 0,9 3 = 0,729;
P₃(1) = С₃ 1 p 1 q 3-1 = 3*0,1*0,9 2 = 0,243;
P₃(2) = С₃ 2 p 2 q 3-2 = 3*0,1 2 *0,9 = 0,027;
P₃(3) = С₃ 3 p 3 q 3-3 = р 3 =0,1 3 = 0,001;
Проверка: ∑p_i = 0,729+0,243+0,027+0,001=1.

Таким образом, искомый биномиальный закон распределения Х имеет вид:

Значения xi	0	1	2	3
Вероятности pi	0,729	0,243	0,027	0,001

2. Для построения многоугольника распределения строим прямоугольную систему координат.

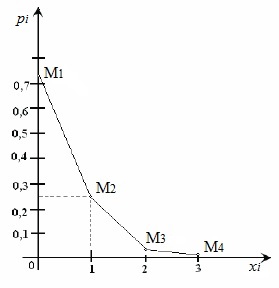По оси абсцисс откладываем возможные значения х_i, а по оси ординат – соответствующие им вероятности р_i. Построим точки М₁(0; 0,729), М₂(1; 0,243), М₃(2; 0,027), М₄(3; 0,001). Соединив эти точки отрезками прямых, получаем искомый многоугольник распределения.

3. Найдем функцию распределения F(x) = Р(Х 3 будет F(x) = 1, т.к. событие достоверно.

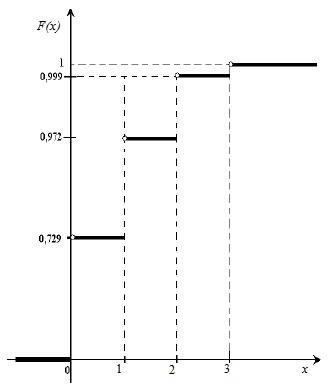— график функции F(x)

4. Для биномиального распределения Х:
— математическое ожидание М(X) = np = 3*0,1 = 0,3;
— дисперсия D(X) = npq = 3*0,1*0,9 = 0,27;
— среднее квадратическое отклонение σ(X) = √D(X ) = √0,27 ≈ 0,52.

Другие статьи по данной теме:

Список использованных источников

1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике / М. — «Высшая школа», 2004;
2. Лисьев В.П. Теория вероятностей и математическая статистика: Учебное пособие/ Московский государственный университет экономики, статистики и информатики. – М., 2006;
3. Семёнычев В. К. Теория вероятности и математическая статистика: Лекции /Самара, 2007;
4. Теория вероятностей: контрольные работы и метод. указания для студентов / сост. Л.В. Рудная и др. / УрГЭУ — Екатеринбург, 2008.

2012 © Лана Забродская. При копировании материалов сайта ссылка на источник обязательна

Источник

Законы распределения дискретных случайных величин

Можно выделить наиболее часто встречающиеся законы распределения дискретных случайных величин:

• Биномиальный закон распределения
• Пуассоновский закон распределения
• Геометрический закон распределения
• Гипергеометрический закон распределения

Для данных распределений дискретных случайных величин расчет вероятностей их значений, а также числовых характеристик (математическое ожидание, дисперсия, и т.д.) производится по определенных «формулам». Поэтому очень важно знать данные типы распределений и их основные свойства.

1. Биномиальный закон распределения.

Дискретная случайная величина $X$ подчинена биномиальному закону распределения вероятностей, если она принимает значения $0,\ 1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)=C^k_n\cdot p^k\cdot <\left(1-p\right)>^$. Фактически, случайная величина $X$ — это число появлений события $A$ в $n$ независимых испытаний Бернулли. Закон распределения вероятностей случайной величины $X$:

$\begin<|c|c|>
\hline
X_i & 0 & 1 & \dots & n \\
\hline
p_i & P_n\left(0\right) & P_n\left(1\right) & \dots & P_n\left(n\right) \\
\hline
\end$

Для такой случайной величины математическое ожидание $M\left(X\right)=np$, дисперсия $D\left(X\right)=np\left(1-p\right)$.

Пример. В семье двое детей. Считая вероятности рождения мальчика и девочки равными $0,5$, найти закон распределения случайной величины $\xi $ — числа мальчиков в семье.

Пусть случайная величина $\xi $ — число мальчиков в семье. Значения, которые может принимать $\xi :\ 0,\ 1,\ 2$. Вероятности этих значений можно найти по формуле $P\left(\xi =k\right)=C^k_n\cdot p^k\cdot <\left(1-p\right)>^$, где $n=2$ — число независимых испытаний, $p=0,5$ — вероятность появления события в серии из $n$ испытаний. Получаем:

Тогда закон распределения случайной величины $\xi $ есть соответствие между значениями $0,\ 1,\ 2$ и их вероятностями, то есть:

Сумма вероятностей в законе распределения должна быть равна $1$, то есть $\sum _^P(\xi _<<\rm i>> )=0,25+0,5+0,25=1 $.

Математическое ожидание $M\left(\xi \right)=np=2\cdot 0,5=1$, дисперсия $D\left(\xi \right)=np\left(1-p\right)=2\cdot 0,5\cdot 0,5=0,5$, среднее квадратическое отклонение $\sigma \left(\xi \right)=\sqrt=\sqrt<0,5>\approx 0,707$.

2. Закон распределения Пуассона.

Если дискретная случайная величина $X$ может принимать только целые неотрицательные значения $0,\ 1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)=<<<\lambda >^k>\over >\cdot e^<-\lambda >$, то говорят, что она подчинена закону распределения Пуассона с параметром $\lambda $. Для такой случайной величины математическое ожидание и дисперсия равны между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda $.

Замечание. Особенность этого распределения заключается в том, что мы на основании опытных данных находим оценки $M\left(X\right),\ D\left(X\right)$, если полученные оценки близки между собой, то у нас есть основание утверждать, что случайная величина подчинена закону распределения Пуассона.

Пример. Примерами случайных величин, подчиненных закону распределения Пуассона, могут быть: число автомашин, которые будут обслужены завтра автозаправочной станцией; число бракованных изделий в произведенной продукции.

Пример. Завод отправил на базу $500$ изделий. Вероятность повреждения изделия в пути равна $0,002$. Найти закон распределения случайной величины $X$, равной числу поврежденных изделий; чему равно $M\left(X\right),\ D\left(X\right)$.

Пусть дискретная случайная величина $X$ — число поврежденных изделий. Такая случайная величина подчинена закону распределения Пуассона с параметром $\lambda =np=500\cdot 0,002=1$. Вероятности значений равны $P\left(X=k\right)=<<<\lambda >^k>\over >\cdot e^<-\lambda >$. Очевидно, что все вероятности всех значений $X=0,\ 1,\ \dots ,\ 500$ перечислить невозможно, поэтому мы ограничимся лишь первыми несколькими значениями.

Закон распределения случайной величины $X$:

Для такой случайной величины математическое ожидание и дисперсия равным между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda =1$.

3. Геометрический закон распределения.

Если дискретная случайная величина $X$ может принимать только натуральные значения $1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)=p<\left(1-p\right)>^,\ k=1,\ 2,\ 3,\ \dots $, то говорят, что такая случайная величина $X$ подчинена геометрическому закону распределения вероятностей. Фактически, геометрическое распределения представляется собой испытания Бернулли до первого успеха.

Пример. Примерами случайных величин, имеющих геометрическое распределение, могут быть: число выстрелов до первого попадания в цель; число испытаний прибора до первого отказа; число бросаний монеты до первого выпадения орла и т.д.

Математическое ожидание и дисперсия случайной величины, подчиненной геометрическому распределению, соответственно равны $M\left(X\right)=1/p$, $D\left(X\right)=\left(1-p\right)/p^2$.

Пример. На пути движения рыбы к месту нереста находится $4$ шлюза. Вероятность прохода рыбы через каждый шлюз $p=3/5$. Построить ряд распределения случайной величины $X$ — число шлюзов, пройденных рыбой до первого задержания у шлюза. Найти $M\left(X\right),\ D\left(X\right),\ \sigma \left(X\right)$.

Пусть случайная величина $X$ — число шлюзов, пройденных рыбой до первого задержания у шлюза. Такая случайная величина подчинена геометрическому закону распределения вероятностей. Значения, которые может принимать случайная величина $X:$ 1, 2, 3, 4. Вероятности этих значений вычисляются по формуле: $P\left(X=k\right)=pq^$, где: $p=2/5$ — вероятность задержания рыбы через шлюз, $q=1-p=3/5$ — вероятность прохода рыбы через шлюз, $k=1,\ 2,\ 3,\ 4$.

Тогда ряд распределения случайной величины $X$:

$\begin<|c|c|>
\hline
X_i & 1 & 2 & 3 & 4 \\
\hline
P\left(X_i\right) & 0,4 & 0,24 & 0,144 & 0,216 \\
\hline
\end$

$M\left(X\right)=\sum^n_=1\cdot 0,4+2\cdot 0,24+3\cdot 0,144+4\cdot 0,216=2,176.$

Среднее квадратическое отклонение:

4. Гипергеометрический закон распределения.

Если $N$ объектов, среди которых $m$ объектов обладают заданным свойством. Случайных образом без возвращения извлекают $n$ объектов, среди которых оказалось $k$ объектов, обладающих заданным свойством. Гипергеометрическое распределение дает возможность оценить вероятность того, что ровно $k$ объектов в выборке обладают заданным свойством. Пусть случайная величина $X$ — число объектов в выборке, обладающих заданным свойством. Тогда вероятности значений случайной величины $X$:

Замечание. Статистическая функция ГИПЕРГЕОМЕТ мастера функций $f_x$ пакета Excel дает возможность определить вероятность того, что определенное количество испытаний будет успешным.

$f_x\to $ статистические $\to $ ГИПЕРГЕОМЕТ $\to $ ОК. Появится диалоговое окно, которое нужно заполнить. В графе Число_успехов_в_выборке указываем значение $k$. Размер_выборки равен $n$. В графе Число_успехов_в_совокупности указываем значение $m$. Размер_совокупности равен $N$.

Математическое ожидание и дисперсия дискретной случайной величины $X$, подчиненной геометрическому закону распределения, соответственно равны $M\left(X\right)=nm/N$, $D\left(X\right)=<\over >\right)\left(1-<\over >\right)>\over >$.

Пример. В кредитном отделе банка работают 5 специалистов с высшим финансовым образованием и 3 специалиста с высшим юридическим образованием. Руководство банка решило направить 3 специалистов Для повышения квалификации, отбирая их в случайном порядке.

а) Составьте ряд распределения числа специалистов с высшим финансовым образованием, которые могут быть направлены на повышение квалификации;

б) Найдите числовые характеристики этого распределения.

Пусть случайная величина $X$ — число специалистов с высшим финансовым образованием среди трех отобранных. Значения, которые может принимать $X:0,\ 1,\ 2,\ 3$. Данная случайная величина $X$ распределена по гипергеометрическому распределению с параметрами: $N=8$ — размер совокупности, $m=5$ — число успехов в совокупности, $n=3$ — размер выборки, $k=0,\ 1,\ 2,\ 3$ — число успехов в выборке. Тогда вероятности $P\left(X=k\right)$ можно рассчитать по формуле: $P(X=k)=^ \cdot C_^ \over C_^ > $. Имеем:

Тогда ряд распределения случайной величины $X$:

$\begin<|c|c|>
\hline
X_i & 0 & 1 & 2 & 3 \\
\hline
p_i & 0,018 & 0,268 & 0,536 & 0,179 \\
\hline
\end$

Рассчитаем числовые характеристики случайной величины $X$ по общим формулам гипергеометрического распределения.

Источник