Закон распределения дискретной случайной величины способы его задания

Закон распределения дискретной случайной величины. Примеры решения задач

Как известно, случайной величиной называется переменная величина, которая может принимать те или иные значения в зависимости от случая. Случайные величины обозначают заглавными буквами латинского алфавита (X, Y, Z), а их значения – соответствующими строчными буквами (x, y, z). Случайные величины делятся на прерывные (дискретные) и непрерывные.

Дискретной случайной величиной называется случайная величина, принимающая лишь конечное или бесконечное (счетное) множество значений с определенными ненулевыми вероятностями.

Законом распределения дискретной случайной величины называется функция, связывающая значения случайной величины с соответствующими им вероятностями. Закон распределения может быть задан одним из следующих способов.

1. Закон распределения может быть задан таблицей:

Значения xi	x1	x2	x3	.	xn
Вероятности pi	p1	p2	p3	.	pn

События X = x_i (i = 1, 2, 3,…,n) являются несовместными и единственно возможными, т.е. они образуют полную систему событий. Поэтому сумма их вероятностей равна единице: р₁+р₂+р₃+…+р_n = ∑p_i =1

2. Закон распределения может быть задан аналитически (формулой) P(X = x_i) = ϕ(x_i). Например:

а) с помощью биномиального распределения: P_n(X=k) = С_n k p k q n-k , 0 0, k = 0, 1, 2, … .

в) с помощью функции распределения F(x), определяющей для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, т.е. F(x) = P(X 2 или D(X) = M(X 2 )−[M(X)] 2 . Разность X–M(X) называют отклонением случайной величины от ее математического ожидания.
Для биномиального распределения D(X)=npq, для распределения Пуассона D(X)=λ

Среднее квадратическое отклонение (стандартное отклонение) σ(X)=√D(X).

Примеры решения задач по теме «Закон распределения дискретной случайной величины»

Задача 1.

Выпущено 1000 лотерейных билетов: на 5 из них выпадает выигрыш в сумме 500 рублей, на 10 – выигрыш в 100 рублей, на 20 – выигрыш в 50 рублей, на 50 – выигрыш в 10 рублей. Определить закон распределения вероятностей случайной величины X – выигрыша на один билет.

Решение. По условию задачи возможны следующие значения случайной величины X: 0, 10, 50, 100 и 500.

Число билетов без выигрыша равно 1000 – (5+10+20+50) = 915, тогда P(X=0) = 915/1000 = 0,915.

Аналогично находим все другие вероятности: P(X=0) = 50/1000=0,05, P(X=50) = 20/1000=0,02, P(X=100) = 10/1000=0,01, P(X=500) = 5/1000=0,005. Полученный закон представим в виде таблицы:

Значения xi	0	10	50	100	500
Вероятности pi	0,915	0,05	0,02	0,01	0,005

Задача 2.

Найти математическое ожидание числа очков, выпадающих при бросании игральной кости.

Решение. Случайная величина X числа очков принимает значения 1, 2, 3, 4, 5, 6. Вероятность того, что выпадет одно из данных значений равна 1/6. Закон распределения представим в виде таблицы:

Значения xi	1	2	3	4	5	6
Вероятности pi	1/6	1/6	1/6	1/6	1/6	1/6

Найдем математическое ожидание величины Х: М(Х) = 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = (1+2+3+4+5+6)/6 = 21/6 = 3,5

Задача 3.

Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте, построить многоугольник распределения. Найти функцию распределения F(x) и построить ее график. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины.

Решение. 1. Дискретная случайная величина X= <число отказавших элементов в одном опыте>имеет следующие возможные значения: х₁=0 (ни один из элементов устройства не отказал), х₂=1 (отказал один элемент), х₃=2 (отказало два элемента) и х₄=3 (отказали три элемента).

Отказы элементов независимы друг от друга, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, n=3, р=0,1, q=1-р=0,9, определим вероятности значений:
P₃(0) = С₃ 0 p 0 q 3-0 = q 3 = 0,9 3 = 0,729;
P₃(1) = С₃ 1 p 1 q 3-1 = 3*0,1*0,9 2 = 0,243;
P₃(2) = С₃ 2 p 2 q 3-2 = 3*0,1 2 *0,9 = 0,027;
P₃(3) = С₃ 3 p 3 q 3-3 = р 3 =0,1 3 = 0,001;
Проверка: ∑p_i = 0,729+0,243+0,027+0,001=1.

Таким образом, искомый биномиальный закон распределения Х имеет вид:

Значения xi	0	1	2	3
Вероятности pi	0,729	0,243	0,027	0,001

2. Для построения многоугольника распределения строим прямоугольную систему координат.

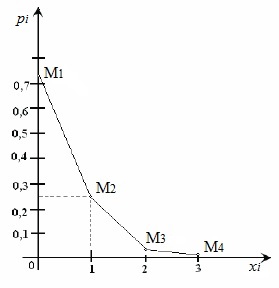По оси абсцисс откладываем возможные значения х_i, а по оси ординат – соответствующие им вероятности р_i. Построим точки М₁(0; 0,729), М₂(1; 0,243), М₃(2; 0,027), М₄(3; 0,001). Соединив эти точки отрезками прямых, получаем искомый многоугольник распределения.

3. Найдем функцию распределения F(x) = Р(Х 3 будет F(x) = 1, т.к. событие достоверно.

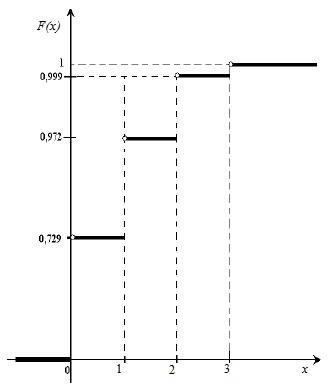— график функции F(x)

4. Для биномиального распределения Х:
— математическое ожидание М(X) = np = 3*0,1 = 0,3;
— дисперсия D(X) = npq = 3*0,1*0,9 = 0,27;
— среднее квадратическое отклонение σ(X) = √D(X ) = √0,27 ≈ 0,52.

Другие статьи по данной теме:

Список использованных источников

1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике / М. — «Высшая школа», 2004;
2. Лисьев В.П. Теория вероятностей и математическая статистика: Учебное пособие/ Московский государственный университет экономики, статистики и информатики. – М., 2006;
3. Семёнычев В. К. Теория вероятности и математическая статистика: Лекции /Самара, 2007;
4. Теория вероятностей: контрольные работы и метод. указания для студентов / сост. Л.В. Рудная и др. / УрГЭУ — Екатеринбург, 2008.

2012 © Лана Забродская. При копировании материалов сайта ссылка на источник обязательна

Источник

Закон распределения вероятностей дискретной случайной величины

Дата добавления: 2013-12-23 ; просмотров: 7587 ; Нарушение авторских прав

Определение2.1:Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.

Способы задания дискретной случайной величины

1) Для задания дискретной случайной величины достаточно задать семейство вероятностей p_i = P(X = x_i), где или .

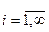
2) Табличный способ задания дискретной случайной величины: первая строка таблицы содержит возможные значения случайной величины, расположенные в порядке возрастания, а вторая – их вероятности:

X	x1	x2	x3	…..	xn
P	p1	p2	p3	…..	pn

Сумма вероятностей второй строки таблицы равна единице:

(условие нормировки).

Замечание1: В одном испытании случайная величина X принимает одно и только одно возможное значение, следовательно, события (X = x_i), где образуют полную группу.

Замечание2: Если множество возможных значений бесконечно (счетно), то ряд 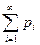сходится и его сумма равна единице.

3) Многоугольник распределения или графический способ задания дискретной случайной величины.

В прямоугольной системе координат строят точки ( x_i , p_i ), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

4) Задать закон распределения дискретной случайной величины можно в виде функции распределения вероятностей (интегральной функции распределения) F(x).

Пример.В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 10000 рублей и десять выигрышей по 1000 рублей. Найти ряд распределения, функцию распределения случайной величины X – стоимости возможного выигрыша для владельца одного лотерейного билета. Построить многоугольник распределения.

Решение: Случайная величина X принимает значения 0,1000,10000с вероятностями:

, , .Таким образом, ряд распределения имеет следующий вид:

X
P	0,89	0,1	0,01

Условие нормировки выполняется: .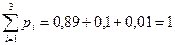

Источник

Закон распределения дискретной случайной величины способы его задания

Случайной называется величина, которая в результате испытания может принять то или иное числовое значение, причем заранее неизвестно, какое именно.

Если для какой- либо величины ее измерение повторять многократно в практически одинаковых условиях, то обнаружится, что всякий раз получаются несколько отличные друг от друга результаты. Это складывается влияние причин двух видов: 1) основных, определяющих главное значение результата; 2) второстепенных, обуславливающих их расхождение.

При совместном действии этих причин понятия необходимости и случайности оказываются тесно связанными между собой, но необходимое преобладает над случайным.

Таким образом, возможные значения случайных величин принадлежат некоторым числовым множествам.

Случайным является то, что на этих множествах величины могут принять любое значение, но какое именно, заранее сказать нельзя.

Случайная величина связана со случайным событием.

Если случайное событие — качественная характеристика испытаний, то случайная величина — его количественная характеристика.

Законы распределения могут быть заданы тремя способами: табличным, графическим, аналитическим. Способ задания зависит от типа случайной величины.

Различают два основных типа случайных величин: дискретные и непрерывно распределенные случайные величины.

Источник

Лекция «Дискретная случайная величина, закон ее распределения. Числовые характеристики дискретной случайной величины»

« Дискретная случайная величина, закон ее распределения. Числовые характеристики дискретной случайной величины »

1. Закон распределения ДСВ:

Случайная величина. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Например, число бракованных лампочек среди 10 купленных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2,….,10. Случайные величины обозначаются прописными буквами латинского алфавита: X , Y , Z и так далее, а их значения – соответствующими строчными буквами x , y , z и так далее.

Различают дискретные и непрерывные случайные величины.

Случайная величина называется дискретной, если множество её значений конечно или счетно, то есть множество её значений представляет собой конечную последовательность x ₁ , x ₂ ,…. x _n или бесконечную последовательность x ₁ , x ₂ . x _{n ,} …

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного множества. Число возможных значений непрерывной случайной величины бесконечно.

Например, если в качестве случайной величины рассматривать оценку студента на экзамене, то с определенной вероятностью, которая зависит от многих факторов, студент может получить или 2, или 3, или 4, или 5, но в результате сданного одним студентом экзамена в ведомости всегда стоит только одна оценка.

Случайная величина может быть задана законом распределения .

Законом распределения дискретной случайной величины (сокращенно ДСВ) называют соответствие между возможными значениями и их вероятностями.

Закон распределения дискретной случайной величины можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины таблица состоит из двух строк и называется законом или рядом распределения дискретной случайной величины X. Первая строка таблицы содержит возможные значения случайной величины, а вторая — соответствующие им вероятности.

Значения записываются в таблице, как правило, в порядке возрастания. Приняв во внимание, что в каждом отдельном испытании случайная величина принимает только одно возможное значение случайной величины X, заключаем, что события несовместны и образуют полную группу событий. Следовательно, сумма вероятностей этих событий, т.е. сумма вероятностей второй строки таблицы, равна единице:

В издательстве выпущено 100 книг по овцеводству. Лотереей разыграны одна книга в 500 руб. и 10 по 10 руб. Найти закон распределения случайной величины х — возможного выигрыша одной книги.

2. Числовые характеристики дискретной случайной величины:

Функцией распределения случайной величины называют функцию F ( x ), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х, то есть F ( x ) = P ( X x ).

Кроме закона распределения, который дает полное представление о случайной величине, часто используют числа, которые описывают случайную величину суммарно. Такие числа называют числовыми характеристиками случайной величины. К ним относятся математическое ожидание, дисперсия и среднее квадратичное отклонение дискретной случайной величины .

Математическим ожиданием (М) дискретной величины называют сумму произведений всех ее возможных значений, умноженных на их вероятности.

где x _i , — значение случайной величины, p _i — вероятность случайной величины.

Математическое ожидание дискретной случайной величины обладает свойствами , которые вытекают из его определения.

1. Математическое ожидание постоянной величины С есть постоянная величина

2. Математическое ожидание дискретной случайной величины X, умноженной на постоянную величину С, равно произведению математического ожидания М(Х) на С. То есть постоянный множитель можно выносить за знак суммирования

3. Математическое ожидание суммы дискретных случайных величин X и У равно сумме их математических ожиданий.

4. Математическое ожидание произведения независимых дискретных случайных величин X и Y равно произведению их математических ожиданий

Часто требуется оценить рассеяние возможных значений случайной величины вокруг его среднего значения. Дисперсией (рассеянием) D ( x ) случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D ( X ) = М[Х -М(Х)] 2 .

Средним квадратичным отклонением ( (х)) случайной величины х называют квадратный корень из дисперсии: ( х )

Исследование вариационных статистических рядов рассмотрим на примере.

Пример: Дан дискретный вариационный ряд

Провести исследование дискретного вариационного ряда

1) найти объём выборки;

2) составить закон распределения случайной величины X ;

3) найти математическое ожидание, дисперсию и среднее квадратичное отклонение.

Закон распределения случайной величины X представлен таблицей:

3) Найдём математическое ожидание, дисперсию и среднее квадратичное отклонение:

Источник

Читайте также:  Способы по энергосбережению электроэнергия