Задайте различными способами множество первых десяти натуральных чисел

Источник

Множества

Введение в теорию множеств

Теоретико-множественные представления — описание иссле­дуемой системы, процессов средствами теории множеств, т.е. как множества взаимосвязанных и/или взаимодействующих частей — элементов. Связи между элементами задаются через отношения и/или соответствия. Множества, элементы, отношения, соот­ветствия характеризуются определенными свойствами и набо­ром допустимых операций над ними.

Состав объекта исследования может быть представлен в виде дискретного множества. Множество — основное поня­тие в теории множеств, которое вводится без определения.

Множество—состоит из элементов. Принадлежность элемента а множеству М обозначается а М («а принадлежит М«), непринадлежность — аМ или аМ .

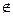
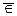
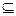
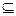
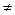
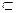
Множество А называется подмножеством множества В (обозначается АВ), если всякий элемент из А является элементом В (рис 1.1). Если АВ и АВ, то А называется строгим (собственным) подмножеством (обозначается АВ).

Примерыобозначения числовых множеств:

N – <1, 2, 3, …>– множество натуральных чисел,

N₀ – <0, 1, 2, 3, …>– множество неотрицательных целых чисел,

R – множество действительных чисел.

Два определения равенства множеств:

I. Множества А и В равны (А=В>, если их элементы совпадают.

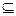
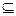
П. Множества А и В равны, если АВ и ВА.

Множество, состоящее из конечного числа элементов, на­зывается конечным, в противном случае — бесконечным (например, множества N, R — бесконечные множества). Число элементов в конечном множестве М называется его мощностью и обозначается \М\.

Множество мощности 0, т.е. не содержащее элементов, называется пустым (обозначается Ø): |Ø| =0. Принято считать, что пустое множество является подмножеством любого множества.

Способы задания множеств:

• Перечислением, т.е. списком своих элементов. Списком можно задать лишь конечные множества. Обозначение списка — в фигурных скобках. Например, множество А устройств домашнего компьютера, состоящего из системного блока а, а также периферийных устройств В (монитора b, клавиатуры с и принтера d), может быть представлено списком:

• Порождающей процедурой, которая описывает способ получения элементов множества из уже полученных элементов либо других объектов. В таком случае элементами мно­жества являются все объекты, которые могут быть построены с помощью такой процедуры.

Например, множество всех целых чисел, являющихся степенями двойки М₂ n , nN, где N-множество натуральных чисел, (допустимое обозначение М₂ n = 1, 2, 4, 8, 16. ) может быть представлено порождающей процедурой, заданной двумя правилами:

а) 1М₂ n ;

б) если тМ₂ n _n, то 2тМ₂ n

• Описанием характеристических свойств, которыми должны обладать его элементы; обозначается:

М= <х| Р(х)> или М= <х:P(x) >.

«Множество М состоит из элементов х таких, что х обладает свойством Р»).

Например, множество А периферийных устройств персонального компьютера может быть определено:

А = <х: х - периферийное устройство персонального компьютера>.

Если свойство элементов множества М может быть опи­сано коротким выражением, это упрощает его символьное представление. Например, множество всех натуральных четных чисел М_2п может быть представлено:

Пример 1.Задать различными способами множество N всех натуральных чисел: 1,2,3, .

Списком множество N задать нельзя ввиду его бесконечности.

Порождающая процедура содержит два правила:

а) 1N;

б) если nN, то n+1N.

Описание характеристического свойства элементов множества N:

N= <х:х- целое положительное число>.

Пример2. Задать различными способами множество М всех четных чисел 2, 4, 6, . не превышающих 100.

а)2М_2n;

б) если nN, то (n+2)М_2n;

в) n98.

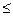
М_2n = <п:п- целое положительное число, не превышающее 100> или М_2п = <п:пN и n/2N, n100>.

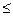
Пример 3. Какие из приведенных определений множеств A, B, C, D являются корректными:

1. Определение множества A= <1,2,3>списком своих элементов формально корректно.

2. При перечислении элементов множества не следует указывать один и тот же элемент несколько раз. Корректное определение B=<5,6,7>.

3. Определение множества C=<х:хА> заданием характеристического свойства его элементов «принадлежать множеству А» корректно.

4. Определние списком множества D=<A,C> корректно.

Пример 4. Пары (1,2) и (2,1) не совпадают, хотя множества <1,2>и <2,1>равны.

Пример 5. Покажем, что множества М₁ = и М₂ = Z> совпадают.

Если хМ₁, то х является решением уравнения sin x=1. Но это значит, что х можно представить в виде x=π/2+2kπ и поэтому хМ₂. Таким образом, М₁ М₂. Если же хМ₂, т. е. x=π/2+2kπ, то sin x=1, т.е. М₂ М₁. Следовательно М₁=М₂.

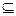
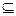
Источник

Задайте различными способами множество первых десяти натуральных чисел

Введение в теорию множеств и комбинаторику

Практическая работа № 1. Способы задания множеств

Вопросы к работе

1. Какие множества называются конечными, какие бесконечными, какие пустыми? Приведите примеры конечных, бесконечных, пустых множеств.

2. Что значит задать множество?

3. Что значит задать множество пересечением элементов? Когда это можно сделать? Приведите пример множеств, заданных пересечением элементов.

4. Что значит задать множество указанием характеристического свойства элементов? Приведите примеры множеств, заданных указанием характеристического свойства элементов.

5. Дайте определение характеристического свойства элементов множества.

Образцы решения заданий

Пример 1. Задать с помощью характеристического свойства элементов множество всех положительных чисел.

Ответ: .

Пример 2. Задать перечислением элементов множества, заданные указанием характеристического свойства элементов:

. Ответ: М = <1; 2; 3; 4>.

Пример 3. Указать стандартное обозначение множества М и изобразить его на числовой прямой:

1. Приведите примеры множеств, составленных из объектов следующих видов:

а) неодушевленных предметов;

г) геометрических фигур;

д) населенных пунктов;

ж) политических деятелей.

2. Назовите элементы, принадлежащие множеству:

а) студентов вашей группы;

б) предметов, изучаемых в I семестре вашей специальности;

в) всех частей света;

г) субъектов федерации, входящих в Российскую Федерацию.

3. Пусть А – множество многоугольников. Принадлежат ли этому множеству:

4. Множество С состоит из квадрата, круга и треугольника. Принадлежит ли этому множеству диагональ квадрата?

5. Прочитайте запись и укажите, какие из указанных высказываний истина, а какие ложь:

а) 270 N ; ж) -3 Z ;

б) 0 N ; з) Q ;

в) –3 N ; и) R ;

г) 1 Q ; к) sin 2,3 R ;

д) –7 N ; л) tg R .

е) 22 N ;

6. Пусть Е – множество европейских государств, А – множество азиатских государств. Какие из следующих высказываний истина, а какие – ложь?

а) Франция Е ; з) Волга Е ;

б) Испания Е ; и) Нигерия А ;

в) Монголия А ; к) Гималаи А ;

г) Индия А ; л) Япония А ;

д) Ирак Е ; м) Альпы Е ;

е) Турция А ; н) Швеция А .

ж) Байкал А ;

7. Запишите перечислением элементов следующие множества:

а) А – множество нечетных чисел на отрезке [1; 15];

б) В – множество натуральных чисел, меньших 8;

в) С – множество натуральных чисел, больших 10, но меньших 12;

г) D – множество двузначных чисел, делящихся на 10;

д) Е – множество натуральных делителей числа 18;

е) F – множество чисел, модуль которых равен .

8. Запишите перечислением элементов следующие множества:

а) множество различных букв в слове «головоломка»;

б) множества цифр числа 134433154.

9. Изобразите на числовой прямой множество решений неравенства с одним неизвестным x :

10. Выясните, множество решений какого неравенства изображено на числовой прямой в каждом случае:

1. Прочитайте следующие записи и перечислите элементы каждого из множеств:

Источник