Задать различными способами множество натуральных чисел кратных 5

Операции над множествами. Задание 1. Задать различными способами множество М3n, всех чисел, являющихся степенями тройки, не превышающих 300

Упражнения.

Задание 1. Задать различными способами множество М₃ n , всех чисел, являющихся степенями тройки, не превышающих 300.

Задание 2. Задать различными способами множество натуральных чисел, кратных пяти: 5, 10, 15, 20 …

Задание 3. Задать различными способами множество М нечетных чисел.

Задание 4. Задать различными способами множество М арабских чисел.

Объединением множеств А и В (обо­значается А 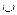В) на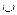зывается множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис 1.2):

А В= <х:хА или хВ>.

Источник

Задать различными способами множество чисел, являющихся степенями 3 и не превышающих 200

Найти количество чисел A (i= 1, 2. n), являющихся степенями m
Даны натуральное число m, n и целые числа а1, а2, . аn. Найти количество чисел аi (i= 1, 2.

Найти количество чисел a1(i=1,2. n), являющихся степенями пятерки
Даны натуральное число n и целые числа а1,а2. аn.Найти количество чисел a1(i=1,2. n),я.

Найти количество чисел, являющихся степенями пятерки
Дана последовательность целых чисел. Длину последовательности задавать с клавиатуры. Числа в.

2) . Здесь обозначает логическое И, а ∃ означает «существует».

Относительно 3) будет лучше, если вы покажете хотя бы один пример задания множества порождающей процедурой из вашего курса.

То, что вы пишете, называется индуктивным (или рекурсивным) определением множества.

Да, можно сказать так (я не уверен, что понял ваши обозначения).

1. .
2. Если и , то .
Других элементов в нет.

Но конечные множества не имеет особого смысла задавать индуктивно. Всегда можно сказать например,

1. .
.
4. .
Других элементов нет.

Создать массив чисел, являющихся степенями числа 2 (от 1 до 5)
Напишите скрипт, который выполняет следующие действия: 1) создает массив чисел, являющихся.

Найти количество чисел, являющихся степенями пятёрки
помогите пожалуйста решить задачу очень надо даны натуральные числа n и целые числа a1, a2. an.

Найти количество чисел, являющихся степенями пятерки
Даны натуральное число n и целые числа a1, a2, . an. Найти количество чисел ai ( i 1, 2, .

Создать и обработать массив чисел, являющихся степенями числа 2 от 1 до 5
Напишите программу, которая выполняет следующие действия: 1) создает массив чисел, являющихся.

Источник

Практические задания к некоторым главам теории множеств

ПРАКТИЧЕСКИЕ ЗАДАНИЯ К НЕКОТОРЫМ ГЛАВАМ ТЕОРИИ МНОЖЕСТВ

1. ПРАКТИЧЕСКИЕ УПРАЖНЕНИЯ ПО ТЕМЕ «СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ»

1. Записать путем перечисления элементов:

а) множество простых чисел первого десятка;

б) множество букв в слове «грамматика»;

в) множество цифр в числе 222222222;

г) множество правильных несократимых дробей со знаменателем 9;

д) множество несократимых дробей с однозначным знаменателем, заключенных между числами 0 и ½;

е) множество десятичных дробей, при записи которых используется цифра 2 три раза, а цифра 5 один раз.

2. Пусть М – множество букв в слове «платок». Является ли подмножеством множества М множество букв в словах: толпа, каток, парта, потолок?

3. Дано множество К = <70, 106, 223, 304>. Составить подмножества множества К из чисел, у которых:

а) цифры десятков четные;

б) цифры десятков являются нечетными;

в) сумма цифр числа равны 7;

г) сумма цифр числа отлична от 7.

4. Какие элементы входят в пересечение и объединение множеств букв в словах:

а) «математика» и «грамматика»;

б) «насос» и «сосна»;

в) «логово» и «голова»;

5. В классе 40 человек. Из них по русскому языку имеют «тройки» 19 человек, по математике – 17 человек и по физике – 22 человека. Четыре человека имеют «тройки» только по русскому языку, 4 – только по математике и 11 человек – только по физике. Семь человек имеют «тройки» по математике и физике. Сколько человек учатся без «троек»? Сколько человек имеют «тройки» по двум из трех предметов? (Решить с помощью кругов Эйлера)

6. Выясните, является ли конечным или бесконечным множество К, и укажите, если возможно, его наименьший и наибольший элементы, зная что:

а) К — множество трехзначных четных чисел;

б) К – множество простых чисел, меньших 30;

в) К – множество натуральных делителей числа 505;

г) К – множество корней уравнения

(х – 2) (х + 11) (х – 12) (х + 13) (х – 14) = 0;

д) К – множество целых чисел, удовлетворяющих условию -4,5 x

е) К – множество целых чисел, удовлетворяющих неравенству | x |

ж) К – множество решений неравенства x > 15;

з) К – множество решений неравенства x

и) К – множество трехзначных чисел, кратных 3;

к) К – множество четырехзначных чисел, кратных 5;

л) К – множество составных чисел, меньших 30;

м) К – множество двузначных чисел, кратных 3.

7. Найдите n ( A ), если:

б) А – множество натуральных делителей числа 28;

в) А – множество трехзначных чисел;

г) А – множество букв в слове «кошка».

8. С – множество цифр в числе 2347. Является ли множество цифр в числе х подмножеством множества С, если:

х = 32; х = 47; х = 43443; х = 27433; х = 43572?

9. А – множество двузначных чисел. Составьте подмножество множества А, в котором каждый элемент – число:

а) оканчивающееся цифрой 9;

б) записанное одинаковыми цифрами.

10. Записать пересечение, объединение, разность множеств X и Y и изобразить кругами Эйлера:

2. ПРАКТИЧЕСКИЕ УПРАЖНЕНИЯ ПО ТЕМЕ «ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ. ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ДЕКАРТОВА ПРОИЗВЕДЕНИЯ»

1. Какую фигуру образуют на координатной плоскости точки, изображающие пары чисел (-1; 0), (-1; 4), (3; 0), (3; 4)?

2. Отметьте штриховкой множество точек координатной плоскости, абсциссы которых отрицательны, а ординаты положительны.

3. Какую фигуру образуют точки, если их абсциссы принадлежат множеству [-2; 2], а ординаты — множеству [-3; 3]?

4. Изобразите декартово произведение в прямоугольной системе координат, если А = <0, 2, 4, 6>, а B = <1, 3, 5>. Принадлежат ли построенной фигуре точки (2; 3), (3; 0)?

5. Изобразить в прямоугольной системе координат множество А × В, если

2) A = [-2; 2], B = [2; 4];

6. Покажите графически, что декартово умножение множеств А = <3, 2, 1>B = <4, 4, 6>не обладает переместительным свойством.

7. Составить декартово произведение множеств M , P и K , если

3. ПРАКТИЧЕСКИЕ УПРАЖНЕНИЯ ПО ТЕМЕ «ОТНОШЕНИЯ МЕЖДУ ЭЛЕМЕНТАМИ МНОЖЕСТВА. СПОСОБЫ ЗАДАНИЯ ОТНОШЕНИЙ»

1.Приведите примеры отношений, существующих между:

а) натуральными числами;

б) прямыми на плоскости;

2. Из элементов множества X = <0, 3, 6, 9, 12, 15, 18>образуйте всевозможные пары чисел так, чтобы компоненты пары ( х; у ) были связаны отношением:

Постройте графы данных отношений.

3.Какое из следующих множеств является отношением между элементами множества A = <0, 3, 6, 9, 12>:

4.На множестве Х = <0, 2, 4, 6, 8>заданы отношения P , Q , S . Составить отношения и постройте их графы, если:

P – отношение «меньше»;

Q – отношение «меньше в два раза»;

S – отношение «меньше на 2».

5.Множество М членов семьи Волковых состоит из отца Михаила Петровича, матери Веры Ивановны и детей: Толи, Кати, Пети и Оли. Между членами семьи существуют различные отношения родства. Постройте графы отношений: 1) «быть дочерью; 2) «быть братом; 3) «быть матерью».

6.Задайте различными способами какое-либо отношение между элементами множества А = <3, 6, 9, 18, 27>.

7. Запишите в виде равенства предложения:

1) число х больше числа у на 5;

2) число х меньше числа у на 7;

3) число х больше числа у в 5 раз;

4) число х меньше числа у в 5 раз.

8.Задайте в виде неравенства с двумя переменными отношения:

1) «меньше»; 2) «меньше или равно».

9.Постройте граф отношения «больше или равно», заданного на множестве <0, 1, 2, 3, 4>. Как задать это отношение при помощи неравенства с двумя переменными?

4. ПРАКТИЧЕСКИЕ УПРАЖНЕНИЯ ПО ТЕМЕ «СВОЙСТВА ОТНОШЕНИЙ»

1. На множестве Х = <1, 2, 4, 8, 12>задано отношение « х кратно у ». Постройте его граф и сформулируйте свойства данного отношения.

2. Чем отличается граф отношения « х –делитель у », заданный на множестве Х (см. упр. 1), от графа отношения « х кратно у »? Есть ли отличия в свойствах этих отношений?

3. Обладает ли свойством рефлексивности отношение «кратно», заданное на множестве В = <0, 2, 4>?

4. На множестве Х = <2, 3, 4, 5, 6>заданы отношения «больше» и «больше или равно». Постройте графы и сформулируйте свойства данных отношений. Какое из них обладает свойством рефлексивности и почему?

5. Каковы свойства отношений «больше в 2 раза» и «больше на 2», заданных на множестве Y = <2, 4, 6, 8, 12>? В чем сходство графов данных отношений?

6. Построили граф отношения R , и оказалось, что он имеет стрелку, идущую от элемента a к элементу b и от элемента b к элементу c , а стрелки, идущей от a к c , нет. Может ли отношение быть транзитивным? Почему?

7. Х – множество прямых плоскости. Какое из следующих отношений является отношением эквивалентности на этом множестве: 1) « х параллельна у »; 2) « х перпендикулярна у »; 3) « х пересекает у »?

8. На множестве Х = <1, 2, 3, 4, 5, 6, 7, 8, 9, 10>задано отношение «иметь один и тот же остаток при делении на 4». Сколько классов эквивалентности определит данное отношение? Запишите эти классы, назовите по одному представителю каждого класса.

9. Объясните, почему отношение равенства отрезков является отношением эквивалентности, а отношение «короче» не является.

10. На множестве Х = <213, 37, 21, 87, 82>задано отношение Р – «иметь в записи одинаковые цифры». Является ли Р отношением эквивалентности?

11. Отношение Т – «иметь одно и то же число делителей» задано на множестве <1, 2, 4, 6, 7, 8, 10, 11>. Покажите, что Т – отношение эквивалентности, запишите все классы эквивалентности.

12. На множестве целых чисел от 0 до 999 задано отношение Р – «иметь в записи одно и то же число цифр». Покажите, что Р – отношение эквивалентности. На сколько классов оно разбивает данное множество чисел? Назовите наименьший и наибольший элементы каждого класса разбиения.

13. Сколько классов эквивалентности определяет на множестве натуральных чисел отношение «оканчиваться одной и той же цифрой»? Назовите по одному представителю каждого класса.

14. Х – множество отрезков. Какие из следующих отношений являются отношениями порядка на этом множестве: 1) « х равно у »; 2) « х длиннее у »; 3) « х короче у на 2см»; 4) « х длиннее у в 3 раза». Упорядочивает ли множество Х отношение «меньше или равно»? Постройте граф этого отношения.

15. Упорядочивает ли множество натуральных чисел отношение «следовать за»? А отношение «непосредственно следовать за»?

16. М – множество окружностей на плоскости, R – отношение «окружность х лежит внутри окружности у ». Упорядочивает ли данное отношение множество М?

5. ПРАКТИЧЕСКИЕ УПРАЖНЕНИЯ ПО ТЕМЕ «СООТВЕТСТВИЯ. ВЗАИМНО ОДНОЗНАЧНЫЕ СООТВЕТСТВИЯ»

1. Даны множества: М = <-1, 1, -2, 2, -3, 3, -4, 4>и N – множество натуральных чисел. Соответствие R между элементами этих множеств – «квадрат числа m равен числу n », причем m принадлежит множеству M , n — элемент множества N .

Соответствие «меньше» задано между элементами множеств А= <1, 2, 4, 6>и B = <5, 7>. Постройте график этого соответствия. Каким будет график соответствия «меньше на 1» между элементами тех же множеств?

Даны множества X = <2, 5>и Y = <3, 6>. Перечислите все элементы декартова произведения данных множеств и образуйте все подмножества полученного множества. Какое из подмножеств задает соответствие: 1) «больше»; 2) «меньше»; 3) «больше или равно»?

4. Множество Р = <(1, 1), (3, 0), (3, 1), (4, 0), (4, 1), (6, 1)>представляет собой соответствие между элементами множеств X = <1, 3, 4, 6>и Y = <0, 1>. Задайте соответствие Р -1 , обратное соответствию Р, и постройте в одной системе координат графики соответствий Р и Р -1 .

5. На множестве Х = <0, 2, 4, 6, 8, 10>задано отношение Т – «число х меньше числа у на 2». Задайте отношение Т -1 и постройте его график на координатной плоскости.

6. Даны множества Х = < k , l , m , n , p >и Y = <1, 2, 3, 4, 5>. Установите три различных взаимно однозначных соответствия между данными множествами. Сколько всего таких соответствий можно установить между множествами Х и Y ?

7. Даны два множества А = <1, 2, 5>и B = <3, 7>. Найдите множества А В и В А. Можно ли каким-либо образом установить взаимно однозначное соответствие между ними?

8. N — множество натуральных чисел, Y – множество квадратов натуральных чисел. Покажите, что между множествами N и Y можно установить взаимно однозначное соответствие.

Источник