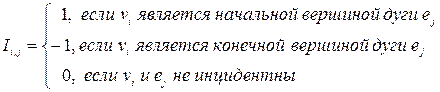Способы задания графов.
Рассмотрим три способа задания графов: графический, аналитический и матричный.
1) Графический способ.
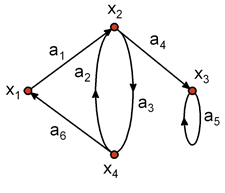
Вершины изображают точками на плоскости, а ребра – линиями, соединяющими соответствующие точки. Для изображения дуги используется линия со стрелкой, указывающей направление от начала к концу дуги.
На рисунке 12 изображен смешанный граф с вершинами v1, v2,¼, v6, ребрами e1, e2, e3, e5 и дугой e4. Смежные вершины v1, v2, инциденты ребру e1. Вершины v1, v3, инциденты параллельным ребрам e2 и e3. Вершине v4 инциденты петля e5 и дуга e4, причем v4 является началом дуги e4, а v5 – концом этой дуги. Степень вершины v1 равна 3, вершины v2 – 1, вершины v3 – 2, вершины v4 – 3, вершины v5 – 1, вершины v6 – 0. Таким образом, вершины v2 и v5 – висячие, а вершина v6 – изолированная. В случае дуги e4 точнее было бы говорить о полустепенях исхода и захода вершин v4 и v5, а именно: полустепень исхода вершины v4 равна 3, вершины v5 – 0, полустепень захода вершины v4 равна 2, вершины v5 – 1.
2) Аналитический способ.
3) Матричный способ.
Имеется несколько вариантов задать граф матрицей. Наиболее употребимыми являются матрица инциденций и матрица смежности.
а) Матрица инциденций – это прямоугольная матрица, число строк которой равно числу вершин, а число столбцов – числу дуг (ребер) графа. Элементы этой матрицы определяются следующим образом:
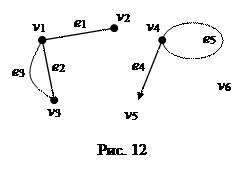
Таким образом, для графа на рисунке 12 матрица инциденций такова:
| e1 | e2 | e3 | e4 | e5 |
| v1 | ||||
| v2 | ||||
| I= | v3 | |||
| v4 | ||||
| v5 | -1 | |||
| v6 |
По этой матрице легко судить о наличии в графе параллельных ребер (два одинаковых столбца), петли (одна единица в столбце), дуги (значения разных знаков в столбце), изолированной вершины (нулевая строка), висячих вершин (одно ненулевое значение в строке).
б) Матрица смежности вершин – это квадратная матрица, размер которой определяется числом вершин в графе. Элементы этой матрицы определяются так: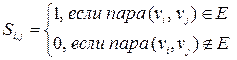 
. Если в графе имеются параллельные ребра, то соответствующий элемент матрицы смежности полагают равным числу этих ребер. Так матрица смежности для графа на рисунке 12 такова:
| v1 | v2 | v3 | v4 | v5 | v6 |
| v1 | |||||
| v2 | |||||
| S= | v3 | ||||
| v4 | |||||
| v5 | |||||
| v6 |
По виду этой матрицы также несложно судить о наличии в графе кратных ребер, дуг, петель, висячих и изолированных вершин.
Дата добавления: 2015-10-19 ; просмотров: 17450 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Способы задания графов
Способы задания графа. Изоморфные графы.
Графы могут задаваться следующими способами:
1) геометрическим способом – рисунки, схемы, диаграммы;
2) алгебраическим способом – перечислением вершин и ребер;
3) табличным способом;
4) матричным способом.
Человеку удобно работать с графом-рисунком, так как он может легко установить связь между вершинами в наглядном виде с помощью ребер, изображаемых непрерывными линиями. Такое геометрическое представление плоского графа называется его реализацией.
Для машинной обработки удобнее задать граф в алгебраической форме – перечислением (списком) вершин или ребер.
При переходе от алгебраического способа к геометрическому одному и тому же графу могут соответствовать различные изображения – изоморфные графы,при этом от правильного изображения зависит, например, свойство плоской реализуемости. Для этого нужно правильно задать сам граф.
Основным способом задания графа является перечисление всех его вершин и ребер. Но такое представление, во-первых, несимметрично, во-вторых, для указания каждого ребра нужно еще раз выписывать соответствующие вершины, что плохо с точки зрения сжатия и хранения информации.
При задании графа таблицейсоставляется таблица,состоящей из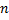 
строк (вершины) и т 
столбцов (ребра). На пересечении строк и столбцов пишутся соответствующие знаки, которые показывают отношение (инцидентность) вершины и ребра. Это может быть знаки “+” и “-”, числа 0,1,-1 и др.
Главным во всех способах задания графа (диаграммой, матрицей, таблицей) является указание соответствия между множествами 
вершин 
t к 
ребер 
.
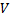
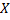
Пусть дан граф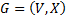 
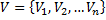
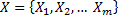
,где 
– вершины, а 
– ребра, среди которых могут и кратные ребра (есть вершины, которые соединяет несколько ребер).
Матрицей инцидентностиданного графа будет таблица, состоящая из 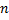строк (вершины) и 
столбцов (ребра).
При рассмотрении неориентированного графа на пересечении строк и столбцов ставится число 1, если соответствующие вершина и ребро инцидентны и ставится число 0, они не инцидентны.
При рассмотрении ориентированного графа на пересечении строк и столбцов ставится число 1, если из вершины выходит соответствующее ее ребро. Если в вершину входит ребро, то ставят число -1. Если вершина не инцидентна ребру, то ставится число 0.
Очевидно, что в каждом столбце матрицы инцидентности должно быть только два ненулевых числа, так как ребро инцидентно двум вершинам. Число ненулевых элементов каждой строки – степень соответствующей вершины.
Матрицы инцидентности прямоугольные, если число строк и столбцов различно. Если число вершин и ребер в графе одинаковое, то получается квадратная матрица.
Матрицу можно сделать квадратной для любого графа без кратных ребер. В таких случаях строки и столбцы изображают вершины. На пересечении строк и столбцов ставится число 1, если соответствующие вершины соединены ребром и ставится число 0, если вершины не соединены.
Для неориентированного графа ребраодновременно принадлежат или не принадлежат графу, так как символизируют одно и то же ребро. Матрица смежности неориентированного графа является симметрической и не меняется при транспонировании.
Хотя формально каждая вершина всегда смежная сама с собой, в матрице смежности мы будем ставить 0, если у нее нет петли, и 1, если есть одна петля.
Если граф имеет матрицу смежности и не имеет петель, на главной диагонали у него всегда стоят нули.
Пример.Составить таблицу инцидентности для орграфа, который имеет 3 вершины и 4 ребра.
| Вершины | Ребра | ||
| s | t | г | и |
| V1 | -1 | ||
| V2 | -1 | ||
| V3 | -1 | -1 |
Граф называется взвешеннымили сетью,если каждому его ребру поставлено в соответствие некоторое число. Взвешенными графами могут быть схемы в электронике, электрические схемы, карты автомобильных и железных дорог и др. Например, на картах автодорог вершины являются населенными пунктами, ребра – дорогами, а весом – числа, равные расстоянию между населенными пунктами.
В основе процесса планирования лежит некоторый сценарий, представляющий собой сеть, состоящую из вершин – пошагового описания действий и дуг – отношений между ними. Такой граф дает возможность, сравнивая альтернативы, планировать действия для достижения поставленной цели.
Понятия-объекты и другие элементы предметной области могут быть графически изображены в виде вершин, а отношения между ними – в виде дуг, связывающих эти вершины.
Источник
Графы и способы их представления
Способы описания графов
Теоретико-множественное представление графов
Граф описывается перечислением множества вершин и дуг. Примеры описания приведены для орграфов на рис. 1.3 и рис. 1.4.
где X =
Задание графов соответствием
Описание графов состоит в задании множества вершин Х и соответствия Г , которое показывает, как между собой связаны вершины.
Соответствием Г называется отображение множества Х в Х , а граф в этом случае обозначается парой G = (X, Г) .
Отображением вершины хi — Г(хi) является множество вершин, в которые существуют дуги из вершины хi , т. е.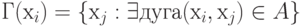 
.
Так для орграфа на рис. 1.3 описание заданием множества вершин и соответствия выглядит следующим образом:
Для неориентированного или смешанного графов предполагается, что соответствие Г задает такой эквивалентный ориентированный граф , который получается из исходного графа заменой каждого неориентированного ребра двумя противоположно направленными дугами, соединяющими те же самые вершины. Например, для графа на рис. 1.2,б Г(х2) = < х1, х3, х5 >, Г(х4) =< х3, х5> и т. д.
Матричное представление графов
Для обработки на ЭВМ графы удобно представлять в виде матриц смежности и инциденций .
Матрица смежности – это квадратная матрица размерностью n x n , (где n – число вершин графа ), однозначно представляющая его структуру.
A =
aij = 1 , если 
дуга (хi, хj) ,
Если элемент на диагонали (i=j) равен единице, значит, вершина i имеет петлю.
Матрица инциденций представляет собой прямоугольную матрицу размером n x m , где n – количество вершин графа , а m – количество дуг графа . Обозначается матрица инциденций B =
Каждый элемент матрицы определяется следующим образом:
bij = 1 , если хi является начальной вершиной дуги aj ,
bij = –1 , если хi является конечной вершиной дуги aj ,
bij = 0 , если хi не является концевой вершиной дуги aj или если aj является петлей.
Таким образом, нулевой столбец j в матрице инциденций свидетельствует о том, что дуга aj яляется петлей.
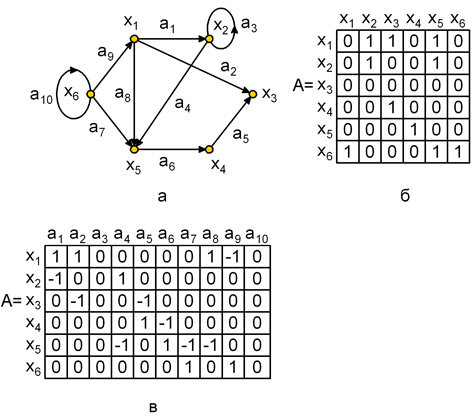
На рис. 1.5, а,б приведен граф и его матрица смежности , по которой можно найти характеристики вершин. Так сумма элементов i -ой строки матрицы дает полустепень исхода вершины хi , а сумма элементов i -го столбца дает полустепень захода вершины хi . По матрице смежности можно найти прямые и обратные отображения. Рассмотрим i -ю строку матрицы. Если элемент aij=1 , то элемент графа хj входит в отображение Г(хi) . Например, во 2-й строке матрицы А ( рис. 1.5,б) единицы стоят в 2-м и 5-м столбцах, следовательно, Г(х2) = < х2, х5> .
Для графа на рис. 1.5,а матрица инциденций приведена на рис. 1.5,в. Поскольку каждая дуга инцидентна двум различным вершинам, за исключением того случая, когда дуга образует петлю, то каждый столбец либо содержит один элемент равный 1 и один – равный – 1, либо все элементы столбца равны 0.
Для неориентированного графа , матрица инциденций определяется так же, за исключением того, что все элементы, равные –1, заменяются на 1.
Источник
