Заданные ниже отношения представить двумя способами

Операции над отношениями

Бинарные отношения

Бинарные отношения служат простым и удобным аппаратом для весьма широкого круга задач. Язык бинарных и n-арных отношений используется во многих прикладных (для математики) областях, например, таких как математическая лингвистика, математическая биология, математическая теория баз данных. Широкое использование языка бинарных отношений легко объясняется — геометрический аспект теории бинарных отношений есть попросту теория графов.

Введем необходимые определения.

Определение 1.1. Декартовым произведением множеств X и Y называется множество XxY всех упорядоченных пар (x, y) таких, что x X, y Y.

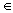
Определение 1.2. Соответствием между множествами X и Y (или соответствием из X в Y) называется любое подмножество декартова произведения XxY. Если множества X и Y совпадают, то соответствие между множествами X и Y называют также бинарным отношением на множестве X.

Отметим, что обычно соответствия задаются не путем указания подмножества a декартова произведения XxY, а путем указания свойства пар (x, y), принадлежащих этому подмножеству

a. Например, отношение a= <(4, 4), (3, 3), (2, 2), (4, 2)> на множестве X = <4, 3, 2> можно определить как свойство «Делится» на этом подмножестве целых чисел.

Хорошо известными примерами отношений из школьного курса математики являются:

· на множестве целых чисел Z отношения «делится», «делит», «равно», «больше», «меньше», «взаимно просты»;

· на множестве прямых пространства отношения «параллельны», «взаимно перпендикулярны», «скрещиваются», «пересекаются», «совпадают»;

· на множестве окружностей плоскости «пересекаются», «касаются», «концентричны».

Факт принадлежности кортежа (x, y) соответствию a, часто обозначают с помощью так называемой инфиксной формы записи: xay. Типичными примерами таких записей из курса математики являются: x > y, a = b, 8 4, m||l, a b и т. п.

Отношения могут задаваться формулами:

y = x 2 +5x — 6 или

задают бинарные отношения на множестве действительных чисел;

задает бинарное отношение на множестве людей. Этому отношению принадлежит любая пара людей, между которыми существует любовь.

Задание отношений в виде формул достаточно широко распространено. Об этом свидетельствуют многочисленные надписи на деревьях заборах или стенах домов типа:

«Вася + Таня = любовь»,

увековечивающие принадлежность конкретной пары (Вася, Таня) отношению «любовь».

Рассмотрим еще три формы представления бинарных отношений: матричное представление и два графических представления. В качестве носителя отношения для иллюстрирующих примеров будем использовать множество X = <a, b, c, d, e>.

Вначале рассмотрим метод, восходящий к аналитической геометрии. Начертим пару взаимно перпендикулярных осей (OX — горизонтальная ось, а OY — вертикальная ось) и на каждой отметим точки, представляющие элементы множества X (рис. 1).

Рис. 1. Координатная сетка

Считая метки a, b, c, d, e координатами точек на горизонтальной и вертикальной осях, отметим на плоскости точки с координатами (x, y) такими, что (x, y) . На рисунке 2 изображено множество точек, соответствующее отношению a= <(a, b), (a, c), (b, d), (c, e), (e,b), (e, e)>.

Рис. 2. Бинарное отношение a

Другой широко распространенный способ представления отношений основан на использовании ориентированных графов. При таком представлении элементы множества X изображаются вершинами графа (точками плоскости), а элементы (x, y) отношения a дугами (стрелками), соединяющими первую компоненту x отношения со второй компонентой y. Граф бинарного отношения a изображен на рисунке 3.

Рис. 3. Граф бинарного отношения

Для бинарных отношений, определенных на конечных множествах, часто используется матричный способ задания. Пусть на некотором конечном множестве X задано отношение a. Упорядочим каким-либо образом элементы множества X = <x₁, x₂, . x_n> и определим матрицу отношения A = [a_ij] следующим образом:

Таким образом, матрица отношения a, представленного графом на рисунке 3, имеет вид

Часто матрицу отношения называют булевой, чтобы подчеркнуть, что ее элементами являются только нули и единицы.

Операции над отношениями

Так как бинарные отношения являются множествами, то к ним применимы все понятия, которые вводятся для множеств: понятие равенства, включения, а также операции пересечения, объединения и дополнения. В этом разделе мы будем считать, что все отношения заданы на одном и том же множестве X.

Пусть a и b — два бинарных отношения на множестве X. Каждому из них соответствует некоторое множество пар (подмножества и ).

Определение 2.1. Пересечением отношений a и b, заданных на множестве X, называется отношение такое, что:

Пример 2.1. Пересечением отношений «не меньше» и «не равно», определенных на множестве действительных чисел R, является отношение «строго больше»:

.

Определение 2.2. Объединением отношений a и b, заданных на множестве X, называется отношение , такое, что:

является отношение «быть ребенком».

Определение 2.3. Разностью отношений a и b, заданных на множестве X, называется отношение a\b, такое, что:

Пример 2.3. Разностью отношений «не меньше» и «не больше» на R является отношение «больше»:

.

Пример 2.4. Разностью отношений «быть ребенком» и «быть дочерью», определенных на множестве всех людей, является отношение «быть сыном».

Определение 2.4. Дополнением отношения a , определенного на множестве X, называется отношение, определяемое подмножеством пар из XxX, не входящих в :

x y .

Пример 2.5. Дополнением отношения «не меньше» на R является отношение «не меньше»:

.

Отметим, что приведенные выше определения являются просто перефразировками соответствующих определений для обычных множеств и все свойства теоретико-множественных операций пересечения, объединения и дополнения, имеющие место для произвольных множеств, выполняются и для отношений.

Кроме теоретико-множественных операций для отношений вводятся некоторые дополнительные операции, которые связаны с их специфической структурой. Мы рассмотрим две такие операции.

Определение 2.5. Если в каждой упорядоченной паре, принадлежащей отношению a, поменять местами первую и вторую компоненты, то получим новое отношение, которое называется обратным для отношения a и обозначается через a -1 :

.

Пример 2.6. Обратным для отношения «не меньше» на множестве действительных чисел R является отношение «меньше»:

.

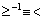
Пример 2.7. Обратным для отношения «быть родителем» на множестве людей является отношение «быть ребенком».

Граф отношения a -1 получается из графа отношения переориентацией всех дуг (рис. 4).

(а) Отношение a (б) Отношение a -1

Рис. 4. Графы отношений a и a -1

Если отношение задано с помощью булевой матрицы, то, поменяв в ней местами строки и столбцы, получим булеву матрицу отношения a -1 (рис 5).

(а) Матрица отношения a (б) Матрица отношения a -1

Рис. 5. Матрицы отношений a и a -1

Определение 2.6. Произведением или композицией отношений a и b, заданных на множестве X, называется отношение a°b, состоящее из таких кортежей (x, z), для которых существует элемент , удовлетворяющий условию и :

.

Пример 2.8. Произведением отношений «быть братом» и «быть отцом» является отношение «быть братом одного из родителей», т. е. «быть дядей».

Если отношения a и b на некотором множестве X заданы с помощью графов, то принадлежность пары (x, z) к отношению a °b означает, что из вершины x в вершину z можно попасть точно за два шага, причем первый из них делается по дуге отношения a , а второй — по дуге отношения b.

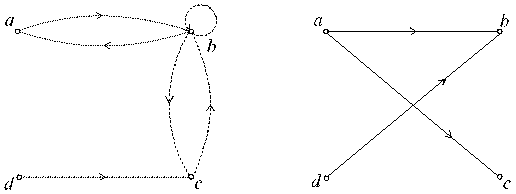
На рисунке 6 изображены графы, представляющие отношения a (точечные дуги) и b (пунктирные дуги), и графы, представляющие произведения отношений a°b и b°a.

(а) Графы отношений a и b (б) Граф отношения a°b

(в) Граф отношения a°b

Рис. 6. Пример произведения отношений (a°b b°a)

Пример, приведенный на рисунке 6, показывает, что для произведения отношений коммутативный закон не выполняется.

Для выражения матрицы произведения двух отношений a и b , заданных булевыми матрицами 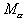и , введем понятие «булево сложение» , определив его следующим образом:

0 0 = 0, 0 1 = 1, 1 0 = 1, 1 1 = 1.

c_ik = a_i1 b_1k … a_in b_nk

Матрица Ma°b называется булевым произведением матриц Ma и Mb. Легко проверить, что Ma°b является булевой матрицей произведения a°b.

Пример 2.9. Вычислим матрицы произведений a°b и b°a отношений a и b , представленных графами на рисунке 6.

Для этого перемножим соответствующие матрицы Ma и Mb (строки и столбцы матриц упорядочены в соответствии с алфавитным порядком букв a, b, c, d, обозначающих вершины графа).

Определим еще одну унарную операцию над отношением.

Определение 2.7. Транзитивным замыканием отношения a называется бинарное отношение такое, что x y тогда и только тогда, когда существует такая цепочка элементов из X:

что между соседями в этой цепочке выполнено отношение a:

Пример 2.10. На рисунке 7 изображены графы, представляющие отношение a и его транзитивное замыкание .

Рис. 7. Транзитивное замыкание отношения a

В матричной форме операция транзитивного замыкания отношения a выражается через объединение степеней матрицы Ma отношения a:

В приведенной формуле объединение матриц понимается следующим образом:

.

Свойства отношений

Очевидно, что произвольные бинарные отношения изучать в общем плане не особенно интересно, о них можно сказать очень мало. Однако, если отношения удовлетворяют некоторым дополнительным условиям, относительно них можно делать более содержательные утверждения. В этом разделе мы рассмотрим некоторые из основных свойств бинарных отношений.

Определение 3.1. Бинарное отношение a на множестве X называется рефлексивным, если для любого элемента a X выполняется условие a a a:

( a X) aa a.

Если отношение представлено с помощью графа, то рефлексивность этого отношения означает, что в каждой вершине графа обязательно имеется петля.

Для отношения, заданного с помощью булевой матрицы его рефлексивность равносильна тому, что по главной диагонали этой матрицы (идущей из ее левого верхнего угла в правый нижний) стоят только символы 1.

Определение 3.2. Бинарное отношение a на X называется антирефлексивным, если ни для одного a X не выполняется условие a a a:

( a X) .

Обозначим через I_x отношение на множестве X, состоящее из пар вида (a, a), где a X:

I_x = <(a, a)| a X>.

Отношение I_x обычно называют диагональю множества X или отношением тождества на X.

Очевидно, что отношение a на множестве X рефлексивно, если диагональ I_x является подмножеством множества a :

I_x a .

Отношение антирефлексивно, если диагональ I_x и отношение a не имеют ни одного общего элемента:

I_x a = O.

Определение 3.3. Бинарное отношение a на множестве X называется симметричным, если из a a b следует b a a:

( a, b X)(aa b baa).

Примерами симметричных отношений являются:

· отношение перпендикулярности на множестве прямых;

· отношение касания на множестве окружностей;

· отношение «быть похожим» на множестве людей;

· отношение «иметь одинаковый пол» на множестве животных.

Отношение «x брат y» на множестве всех людей не является симметричным. В то же время отношение «x брат y» на множестве мужчин симметричным является.

В графе симметричного отношения для каждой дуги из вершины x в вершину y имеется дуга из y в x. Поэтому симметричные отношения можно представлять графами с неориентированными ребрами. При этом каждая пара ориентированных ребер xy и yx заменяется одним неориентированным ребром.

На рисунке 8 представлено отношение

с помощью ориентированного и неориентированного графов.

Рис. 8. Представление симметричного отношения с помощью
ориентированного (a) и неориентированного (b) графов

Матрица симметричного отношения симметрична относительно главной диагонали.

Теорема 3.1. Объединение и пересечение любого семейства симметричных отношений снова являются симметричными отношениями.

Определение 3.4. Бинарное отношение a на множестве X называется антисимметричным, если для любых различных элементов a и b условия a a b и b a a не выполняются одновременно:

( a, b X) (a a b & ba a a = b).

Например, отношение «делится» на множестве натуральных чисел является антисимметричным, так как из a b и b a следует, что a = b. Однако на множестве целых чисел отношение «делится» антисимметричным не является, так как (-2) 2 и 2 (-2), но

-2 2.

Отношения «выше», «тяжелее», «старше» антисимметричны на множестве людей. Отношение «быть сестрой» на множестве всех людей антисимметричным не является.

В графе антисимметричного отношения две различные вершины могут быть соединены не более чем одной дугой.

Определение 3.5. Бинарное отношение a на множестве X называется транзитивным, если для любых трех элементов a, b, c X из aab и bac следует aac:

( a, b, c X) (aa b & ba c aac).

Примерами транзитивных отношений служат:

· отношение «делится» на множестве действительных чисел;

· отношение «больше» на множестве действительных чисел;

· отношение «старше» на множестве людей игрушек;

· отношение «иметь одинаковый цвет» на множестве детских игрушек;

д) отношение «быть потомком» на множестве людей.

Феодальное отношение «быть вассалом» не является транзитивным. Это в частности подчеркивается в некоторых учебниках истории: «вассал моего вассала не мой вассал».

Отношение «быть похожим» на множестве людей не обладает свойством транзитивности.

Для произвольного отношения a можно найти минимальное транзитивное отношение b

такое, что a b. Минимальность отношения понимается в том смысле, что для любого транзитивного отношения g из a g следует b g. Таким отношением является транзитивное замыкание отношения a.

Пример 3.1. Транзитивным замыканием бинарного отношения на множестве людей «быть ребенком» является отношение «быть потомком».

Теорема 3.2. Для любого отношения транзитивное замыкание равно пересечению всех транзитивных отношений, включающих в качестве подмножества.

Определение 3.6. Бинарное отношение a на множестве X называется связным, если для любых двух различных элементов a и b имеет место aab, либо baa:

( a, b, c X)(a b aab baa).

Примером связного отношения является отношение «больше» на множестве действительных чисел. Отношение «делится» на множестве целых чисел связным не является.

4. Инвариантность отношений

В этом параграфе мы перечислим некоторые случаи, когда те или иные свойства отношений сохраняются при выполнении над ними операций [1].

Теорема 4.1. Если отношения a и b рефлексивны, то рефлексивны и следующие отношения:

a b ,b a , a -1 , a°b, .

Теорема 4.2. Если отношения a и b антирефлексивны, то антирефлексивны и следующие отношения:

a b , b a , a -1 .

Теорема 4.3. Если отношения a и b симметричны, то симметричны и следующие отношения:

a b , b a , a -1 .

Теорема 4.4. Чтобы произведение a°b симметричных отношений a и b было симметрично, необходимо и достаточно, чтобы отношения и коммутировали:

Теорема 4.5. Если отношения a и b антисимметричны, то антисимметричны и следующие отношения:

a b , a -1

Теорема 4.6. Если отношения a и b транзитивны, то транзитивны и следующие отношения:

a b , a -1 , .

Другие интересные свойства отношений описаны в [1, 2].

Источник