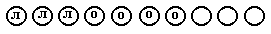Задачу решенную по действиям решите другим способом выражением
СПОСОБЫ РЕШЕНИЯ ЗАДАЧ
Понятие “решение задачи” можно рассматривать с различных точек зрения: решение как результат, т.е. как ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата.
С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который в свою очередь, тоже можно рассматривать с различных точек зрения Во-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, который входят в тот или иной способ.
Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?
Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитывают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т.д. пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ и называется практическим или предметным. Его возможности ограничены, так как учащийся может выполнить предметные действия только с небольшим количеством предметов. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практическим, а арифметическим способом, записав равенство 8 : 2 = 4.
Для решения можно применить алгебраический способ, рассуждая при этом так: “Число тарелок неизвестно, обозначим их буквой Х. На каждой тарелке 2 яблока, значит число всех яблок — это 2х. Так как в условии известно, что число всех яблок 8, то можно записать уравнение 2х = 8 и решить его х = 8 : 2, х = 4”.
Задачи, в которых для ответа на вопрос нужно выполнить только одно действие, называются простыми. Если для ответа на вопрос задачи нужно выполнить два и более действий, то такие задачи называются составными. Составную задачу, так же как и простую можно решить, используя различные способы.
Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?
Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим
пойманных рыб: л — лещи, о — окуни.
Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не обозначены (их З).
1) 3 + 4 = 7 (р.) — пойманные рыбы
Для ответа на вопрос задачи мы выполнили два действия.
Пусть х — пойманные щуки
Тогда количество всех рыб можно записать выражением:
3 + 4 + х — все рыбы
По условию задачи известно, что рыбак поймал всего 10 рыб.
Значит 3 + 4 + х = 10
Решив это уравнение, мы ответим на вопрос задачи.
Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.
В начальных классах используются различные формы записи решения задач по действиям, по действиям с пояснением, с вопросами, выражением.
У мальчика было 90 книг. 28 он поставил на первую полку, 12 на вторую. Остальные на третью. Сколько книг на третьей пилке?
а) решение по действиям
Ответ: 50 книг на третьей полке.
б) по действиям с пояснением
1) 28 + 12 = 40 (к.) на 1 и 2 полках вместе.
2) 90 — 10 = 50 (к.) на 3 полке.
1) Сколько книг на первой и второй полках вместе?
2) Сколько книг на третьей полке?
При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:
90 — (28 + 12) = 50 (к.)
Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.
Например, рассмотренную выше задачу можно решить другим арифметическим способом:
1) 90 — 28 = 62 (к.) на 2 и3 полках.
2) 62 — 12 = 50 (к.) на 3 полке.
В качестве арифметического способа можно рассматривать и такое решение данной задачи:
1) 90 — 12 = 78 (к.) на 2 и 3 полках.
2) 78 -28 = 50 (к.) на З полке.
В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.
Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?
Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:
Ответ: 27 машин было в гараже
В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось не раскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?
Решение задачи можно оформить так:
48 : 3 = 16 (л.) Ответ: 16 листов
[../../../_private/navbar1.htm]
Источник
«Барнаул — 2011 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования АЛТАЙСКАЯ ГОСУДАРСТВЕННАЯ . »
указать) и оцените каждый вариант с точки зрения выполнения данного требования.
7) Определите цели предложенного фрагмента. Как Вы думаете, почему учителем для изображения выбрана такая ситуация?
Учитель предлагает учащимся задание: «Догадайся, как, пользуясь отрезками, изобразить следующую ситуацию — карандаш длиннее ручки Учащиеся работают самостоятельно, а затем различные варианты выполнения задания выносятся на доску и обсуждаются. При наличии одного варианта учитель может предложить свой. Далее анализируются две точки зрения, представленные двумя героями Мишей и Машей и предлагается выбрать правильный вариант.
1 — изобразить эту ситуацию с помощью отрезков нельзя, так как мы не знаем длину ручки;
2 — ситуацию можно изобразить следующим образом:
Учитель говорит о том, что выполненные рисунки будем называть схемами.
8) Используя текст задачи «Сережа поймал 15 рыб, Толя 10. Среди всех рыб было 13 карасей, остальные — окуни. Сколько окуней поймали мальчики?», составьте обучающие упражнения по овладению младшими школьниками схематическим моделированием, ориентируясь на следующие типы:
• выбор среди предложенных моделей той, что соответствует данной задаче;
• выбор среди предложенных задач той, что соответствует данной модели;
• изменение модели в соответствии с требованием;
• запись решения по модели;
• нахождение ошибок в предложенной модели;
• определение по модели всех арифметических способов решения данной задачи.
В случае затруднения рассмотри примеры таких заданий в учебниках математики для начальной школы (автор- Н.Б.Истомина).
Контрольные задания 1) Составьте подготовительные упражнения к введению схемы как вспомогательной модели задачи. Укажите их цели.
2) Используя текст задачи, составьте серию упражнений различных типов (8по обучению младших школьников графическому моделированию.
Выбор моделей и методических приемов обоснуйте.
Масса тыквы в 4 раза больше массы кабачка и на 3 кг меньше массы арбуза. Чему равна масса арбуза, если масса кабачка 2 кг?
ТЕМА №:5 «Методика обучения приемам поиска и выполнения плана решения задачи»
Теоретическая справка Выделяют два основных способа рассуждений, которые помогают найти план решения текстовой задачи.
Синтетический способ рассуждений характеризуется тем, что основным, направляющим вопросом при поиске решения задачи является вопрос о том, что можно найти по двум или нескольким известным в тексте числовым данным. По вновь полученным числовым значениям и другим данным в задаче вновь ищется ответ на вопрос, что можно узнать по этим значениям. И так до ответа на вопрос задачи. Суть этого способа — состоит в вычленении учащимися простой задачи из предложенной составной и решение ее.
Аналитический способ рассуждений характеризуется тем, что рассуждение начинают с вопроса задачи. Выясняется, что нужно предварительно узнать, чтобы ответить на вопрос задачи. Выясняется, что для этого необходимо что-то найти. Вновь ставится вопрос: что нужно знать, чтобы найти «что-то»? и т.д. до того момента, когда ответ на поставленный вопрос имеется в условии задачи. Здесь также в конечном итоге вычленяются простые задачи, но план решения составляется в направлении, противоположном его поиску.
Также можно использовать прием, основанный на анализе данных задачи [4], позволяющий выявить возможные связи между ними, а затем выбрать из них те, что нужны для решения задачи. Суть приема заключается в умении составить выражения из чисел, данных в задаче и разъяснить их смысл. Следует помнить, что поиск плана решения чаще всего осуществляется по модели.
Для обучения данным способам рассуждений (способам разбора задачи) необходимо ориентироваться на следующие этапы(С.Е.Царева):
I. Неявное знакомство с рассуждениями при коллективном решении задач под руководством учителя.
II. Специальное знакомство уч-ся с одним из способов рассуждения.
III. Тренировка в использовании разбора при самостоятельном решении IV. Явное знакомство с другими способами разбора и тренировка в их использовании (аналогично).
V. Самостоятельное использование различных способов рассуждения при решении задач разных видов.
В начальном курсе математики используются различные формы записи решения задачи. Выбор формы определяется в первую очередь тем методом решения, который используется. Для арифметического метода решение задачи можно оформить:
по действиям с пояснением;
по действиям с вопросами;
Литература 1) Артемов А.К. Теоретико-методические особенности поиска способов решения математических задач// начальная школа. 1998. № 11/12.
2) Артемов А.К. Формирование обобщенных умений решать задачи // Начальная школа. 1992. №2.
3) Дополнительные вопросы математики и теоретические основы методики преподавания математики. ч.1.- Барнаул, 1994.
4) Еремеева О.О. Один из приемов поиска решения задачи // Начальная школа. 1994. №4.
5) Лобынцева В.А. Графические схемы// Начальная школа. 1995. №11.
6) Рудакова Е.А., Царева С.Е. Разбор задачи с использованием графических схем // Начальная школа. 1992. №11/12.
7) Семья Ф. Совершенствование работы над составными задачами // Начальная школа. 1991. №5.
8) Царева С.Е. Различные способы решения задач и различные формы записи решения задачи // Начальная школа. 1982. №2.
9) Царева С.Е. Обучение решению задач // Начальная школа. 1998.- №1;
Начальная школа. 1997. № 11.
10) Шикова Р.Н. Способы разбора текстовых задач // Начальная школа.
Вопросы для самоконтроля 1) Раскройте содержание понятия решение задачи в рамках различных методических подходов к обучению решению задач. Какой точки зрения придерживаетесь Вы, почему?
2) Каковы преимущества и недостатки основных приемов поиска плана решения задачи? Можно ли какой-либо из приемов считать универсальным?
От чего зависит выбор приема?
3) Обоснуйте предложенную С.Е.Царевой последовательность обучения основным способам разбора текстовой задачи. Какие условия должны быть созданы учителем при специальном знакомстве учащихся с одним из способов рассуждений?
4) Какие способы или формы записи решения составных задач осваивают младшие школьники? Какой ошибки следует избегать при использовании термина разные способы решения? Чем обусловлен выбор той или формы для записи решения? В какой последовательности необходимо, на Ваш взгляд, вводить основные формы записи решения задачи? Чем это обусловлено?
Задания для самостоятельной работы 1) На примере задачи: “В трех кусках 92 м шнура. В первом 28 м, в третьем 34 м. Сколько метров шнура во втором куске?” проиллюстрировать различные приемы поиска плана решения.
2) Составить памятки для учащихся, которые могут быть использованы для обучения основным приемам поиска плана решения [6].
3) Подготовить беседу по разбору следующих задач с использованием графической схемы разбора:
• В автобусном парке стояло 89 автобусов. Утром выехало в рейс больших автобусов и 30 маленьких. Сколько автобусов осталось в • Шестеро туристов взяли для похода по 2 банки мясных консервов и по 3 овощных. Сколько всего банок консервов взяли туристы?
• Двенадцать килограммов варенья разложили в 6 банок поровну.
Сколько потребуется таких банок, чтобы разложить 24 кг варенья?
4) Составить 2-3 тренировочных упражнения, с помощью которых учащиеся овладевают одним из способов разбора задачи.
5) Определите цели предложенных упражнений. Какие общие умения решать задачи формируются в процессе их выполнения?
• Из каких отрезков состоит искомый отрезок? (Рис. 4) Сумме или разности данных чисел равна его длина?
• Какой отрезок больше и на сколько? (Рис. 5) Какие обозначения нужно ввести, чтобы было понятно, что это схема некоторой текстовой задачи? Введите необходимые обозначения. Составьте план решения этой задачи. (Последовательность операций обосновывается взаимным расположением отрезков, сравнением длин и смыслом обозначений.) Придумайте текст соответствующей задачи. Составьте другую задачу к этой же схеме.
По данным схемам (рис. 6) составьте выражения, значения которых соответствуют знаку «?» на схеме.
6)Одним из эффективных приемов обучения младших школьников составлению плана решения задачи является прием объяснения смысла выражений, составленных по тексту задачи. Объясните способ выполнения следующего задания учащимися. Составьте или подберите из учебников математики для начальной школы аналогичные задания.
Блокнот, линейка и карандаш стоят 27 рублей. Линейка стоит рублей, а карандаш 3 рубля. Сколько стоит блокнот?
• Объясните, что обозначают выражения.
7) Оценить правильность формулировки задания учителя: «Задачу, решенную по действиям, решите другим способом – выражением».
10) Учитель предложил детям задание – решить задачу «У одной закройщицы было 15 м ткани, а у другой – 12 м. Из всей такни они скроили платья, расходуя на каждое по 3 м. Сколько всего платьев они скроили?» разными способами.
Рассмотреть варианты выполнения этого задания двумя учениками. Какой из них верный? Как можно организовать работу над ошибкой?
Контрольные задания 1) Рассмотрите задачу: «Нина нашла 23 желудя, Катя на 6 желудей больше, чем Нина, а Оля на 9 желудей меньше, чем Катя. Сколько желудей нашла Оля?». Составьте фрагмент урока по обучению поиску и выполнению плана решения данной задачи.
2) Разработайте фрагмент урока по введению формы записи решения задачи выражением.
Задания для лабораторных и самостоятельных работ ТЕМА №1: «Методика обучения способам проверки решения текстовых задач».
Теоретическая справка Проверка решения задачи — один из важных этапов работы над задачей.
Цель проверки — установить, соответствует ли процесс и результат решения образцу правильного решения.
В начальном курсе математики могут быть использованы следующие способы проверки решения текстовых задач:
1. Прикидка (прогнозирование результата, установление границ ответа на вопрос задачи и последующее сравнение хода решения с прогнозом) — при несоответствии прогнозу — решение неверно, при соответствии — может быть верно, а может неверно.
2. Установление соответствия между результатом решения и условием задачи (введение в текст задачи вместе вопроса ответа на него, получение всех возможных следствий из полученного текста, сопоставление результатов друг с другом и с информацией, содержащейся в тексте) если обнаружено противоречие, задача решена неверно, и наоборот, однако правильность хода решения не устанавливается.
3. Решение другим методом или способом (результаты должны совпасть)правильность хода решения не устанавливается.
4. Составление и решение обратной задачи (в результат решения должно быть получено данное прямой задачи) — правильность хода решения не устанавливается.
5. Сравнением с правильным решением — с образцом хода и результата решения возможно установление правильности как хода, так и результат решения).
«Министерство образования и науки Российской Федерации ФГАОУ ВПО УрФУ имени первого Президента России Б.Н.Ельцина Ю.Н. Колмогоров, А.П. Сергеев, Д.А. Тарасов, А.Г. Тягунов ОСНОВЫ ОРГАНИЗАЦИИ НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ В ПОЛИГРАФИИ И ВЕБ-ДИЗАЙНЕ Учебное электронное текстовое издание Учебное пособие Подготовлено кафедрой Полиграфия и веб-дизайн Учебно-методическое пособие предназначено для закрепления теоретических и практических навыков слушателей магистратуры по направлению 261700. »
«МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ АКАДЕМИЯ СОЦИАЛЬНОГО УПРАВЛЕНИЯ НАУЧНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ РАЗВИТИЯ ОБРАЗОВАНИЯ В СОВРЕМЕННЫХ УСЛОВИЯХ Сборник научных и методических материалов Под редакцией Л.Н. Антоновой, Г.Б. Корнетова, А.И. Салова АСОУ 2012 УДК 37 ББК 74.04 Н 31 Научно-методическое обеспечение развития образования Н 31 в современных условиях: Сборник научных и методических материалов / Под редакцией Л.Н. Антоновой, Г.Б. Корнетова, А.И. Салова. – АСОУ, 2012. – 280 с. ISBN. »
«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ ГОРНЫЙ УТВЕРЖДАЮ Проректор по научной работе профессор В.Л. ТРУШКО ПРОГРАММА ВСТУПИТЕЛЬНОГО ИСПЫТАНИЯ ПО СПЕЦИАЛЬНОЙ ДИСЦИПЛИНЕ ПЕТРОЛОГИЯ, ВУЛКАНОЛОГИЯ, соответствующей направленности (профилю) направления подготовки научно-педагогических кадров в аспирантуре НАПРАВЛЕНИЕ ПОДГОТОВКИ — 05.06.01. »
«ЧАСТЬ I. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ ЭССЕ ПО ОБЩЕСТВОЗНАНИЮ Общая характеристика задания С8. Содержание контрольно-измерительных материалов Единого государственного экзамена по обществознанию многопланово и многообразно. Каждое задание проверяет знание определенной темы курса и одновременно навыки и умения учащихся. Сейчас появилось много различных пособий, посвященных анализу содержания контрольно-измерительных материалов по обществознанию и методике подготовке к Единому. »
«Министерство образования и науки Российской Федерации Федеральное Государственное образовательное бюджетное учреждение высшего профессионального образования Амурский государственный университет Кафедра Психологии и педагогики УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ Невропатология детского возраста Основной образовательной программы По специальности: 050711.65 Социальная педагогика Благовещенск 2012 УМКд разработан Рассмотрен и рекомендован на заседании кафедры Психологии и педагогики Протокол. »
«Министерство образования и науки РФ Филиал ФГБОУ ВПО Ярославский государственный педагогический университет имени К. Д. Ушинского в г. Рыбинске Ярославской области И. О. Карелина МЕТОДИКА ОБУЧЕНИЯ И ВОСПИТАНИЯ В ОБЛАСТИ ДОШКОЛЬНОГО ОБРАЗОВАНИЯ: КУРС ЛЕКЦИЙ Учебно-методическое пособие Рыбинск 2012 Печатается по решению кафедры теории и методики профессионального образования филиала ЯГПУ в г. Рыбинске Рецензент: кандидат педагогических наук, доцент, Почетный работник среднего профессионального. »
«Министерство образования Республики Беларусь Учреждение образования Белорусский государственный педагогический университет имени Максима Танка Общественное объединение Белорусская ассоциация помощи детям-инвалидам и молодым инвалидам ОБУЧЕНИЕ И ВОСПИТАНИЕ ДЕТЕЙ В УСЛОВИЯХ ЦЕНТРА КОРРЕКЦИОННО-РАЗВИВАЮЩЕГО ОБУЧЕНИЯ И РЕАБИЛИТАЦИИ Учебно-методическое пособие 2-е издание Минск УО БГПУ им. М.Танка 2008 Книга издана в рамках международного проекта Создание национальных информационных центров при. »
«Министерство образования Республики Беларусь УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ ГРОДНЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ ЯНКИ КУПАЛЫ МЕТОДИКА РАБОТЫ СОЦИАЛЬНОГО ПЕДАГОГА Методические рекомендации по одноименному курсу для студентов специальности П 04.03.00 Социальная педагогика Гродно 2004 УДК 66.75(2)5(076) ББК 74 М54 Автор-составитель: М.В. Салтыкова-Волкович, кандидат педагогических наук, ст. преподаватель кафедры социальной и коррекционной педагогики ГрГУ им. Я.Купалы. Рецензенты: кандидат. »
«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ТАТАРСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНО ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ Р.Х. САФАРОВ ФИЗИКА АТОМНОГО ЯДРА И ЭЛЕМЕНТАРНЫХ ЧАСТИЦ (С приложениями к живым системам) 010 К а за н ь 2008 УДК 539.17 ББК 22.38 С 21 Печатается по решению учебно-методического совета физического факультета Татарского государственного гуманитарно педагогического университета Научный редактор: P.M. Юльметьев — доктор физ.-мат. наук, проф. Рецензенты: Ю.А. Нефедьев-д октор физ.-мат. наук. »
«Министерство образования и науки Российской Федерации Федеральное Государственное бюджетное образовательное учреждение высшего профессионального образования Амурский государственный университет Кафедра Психологии и педагогики УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ СОЦИАЛЬНО-ТРУДОВАЯ АДАПТАЦИЯ ДЕТЕЙ ГРУППЫ РИСКА Основной образовательной программы ГОС ВПО по специальности 050711.65 Социальная педагогика Благовещенск 2012 УМКд разработан Т.В. Климовой, старшим преподавателем кафедры Психологии и. »
© 2013 www.dis.konflib.ru — «Бесплатная электронная библиотека»
Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.
Источник
