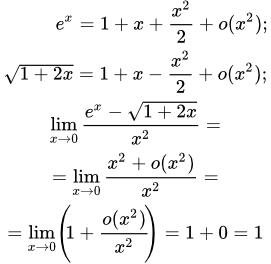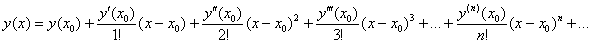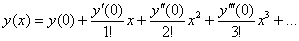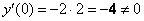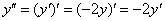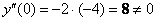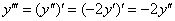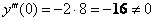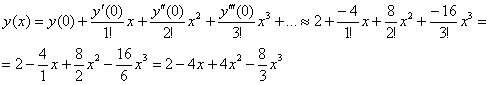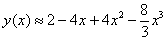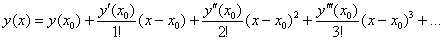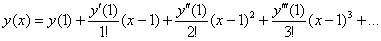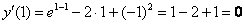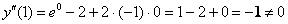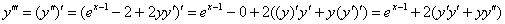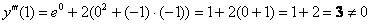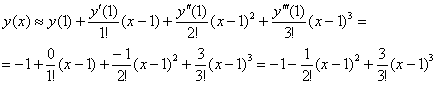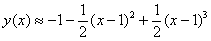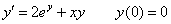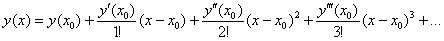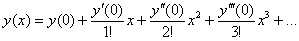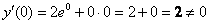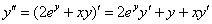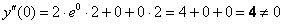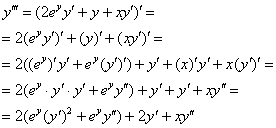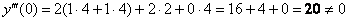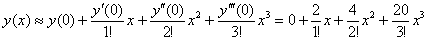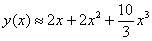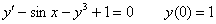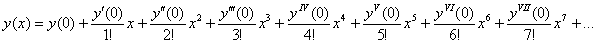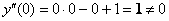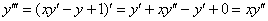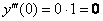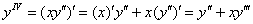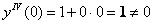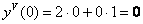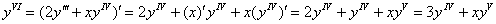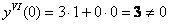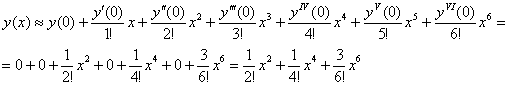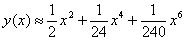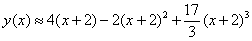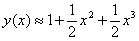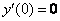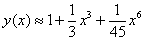Задачи по способу тейлора

Решение пределов, используя ряд Тейлора

Метод решения

Одним из самых мощных методов раскрытия неопределенностей и вычисления пределов является разложение функций в степенной ряд Тейлора. Применение этого метода состоит из следующих шагов.
1) Приводим неопределенность к виду 0/0 при переменной x , стремящейся к нулю. Для этого, если требуется, выполняем преобразования и делаем замену переменной.
2) Раскладываем числитель и знаменатель в ряд Тейлора в окрестности точки x = 0 . При этом выполняем разложение до такой степени x n , которая необходима для устранения неопределенности. Остальные члены включаем в o ( x n ) .

Этот метод применим, если после выполнения пункта 1), функции в числителе и знаменателе можно разложить в степенной ряд.

Выполнять разложение сложных функций и произведения функций удобно по следующей схеме. А) Задаемся показателем степени n , до которого мы будем проводить разложение.
Б) Применяем приведенные ниже формулы разложения функций в ряд Тейлора, сохраняя в них члены до включительно, и отбрасывая члены с при , или заменяя их на .
В) В сложных функциях делаем замены переменных так, чтобы аргумент каждой ее части стремился к нулю при . Например,
.
Здесь при . Тогда можно использовать разложение функции в окрестности точки .

Примечание. Разложение функции в ряд Тейлора, в окрестности точки , называется рядом Маклорена. Поэтому для применяемых в наших целях рядов уместны оба названия.

Применяемые свойства о малого

Определение и доказательство свойств о малого приводится на странице: «О большое и о малое. Сравнение функций». Здесь мы приводим свойства, используемые при решении пределов разложением в ряд Маклорена (то есть при ).

Далее m и n – натуральные числа, .
;
;
, если ;
;
;
;
, где ;
, где c ≠ 0 – постоянная;
.

Для доказательства этих свойств нужно выразить о малое через бесконечно малую функцию:
, где .

Разложение элементарных функций в ряд Тейлора (Маклорена)

Далее приводятся разложения элементарных функций в степенной ряд при . Как мы упоминали ранее, ряд Тейлора в окрестности точки называется рядом Маклорена.

Примеры

Все примеры Далее мы приводим подробные решения следующих пределов с помощью ряда Тейлора.
⇓, ⇓, ⇓, ⇓, ⇓.

Пример 1

Все примеры ⇑ Вычислить предел последовательности, используя разложение в ряд Тейлора.
.

Это неопределенность вида бесконечность минус бесконечность. Приводим ее к неопределенности вида 0/0 . Для этого выполняем преобразования.

.
Здесь мы учли, что номер элемента последовательности n может принимать только положительные значения. Поэтому . Делаем замену переменной . При . Будем искать предел считая, что x – действительное число. Если предел существует, то он существует и для любой последовательности , сходящейся к нулю. В том числе и для последовательности .

.
Раскладываем функцию в числителе в ряд Тейлора. Применяем формулу:
.
Оставляем только линейный член.
.
.
Здесь мы учли, что поскольку существует двусторонний предел , то существуют равные ему односторонние пределы. Поэтому .

Пример 2

Все примеры ⇑ Показать, что значение второго замечательного предела можно получить, используя разложение в ряд Тейлора.

Делаем замену переменной . Тогда . При . Подставляем.
.

Для вычисления предела можно считать, что значения переменной t принадлежат любой, наперед выбранной, проколотой окрестности точки . Мы полагаем, что . Используем то, что экспонента и натуральный логарифм являются обратными функциями по отношению друг к другу. Тогда
.

Вычисляем предел в показателе, используя следующее разложение в ряд Тейлора:
.
.

Поскольку экспонента является непрерывной функцией для всех значений аргумента, то по теореме о пределе непрерывной функции от функции имеем:
.

Пример 3

Все примеры ⇑ Вычислить предел, используя разложение в ряд Тейлора.
.

Это неопределенность вида 0/0 . Используем следующие разложения функций в окрестности точки :
;
;
.

Раскладываем с точностью до квадратичных членов:
;
.
Делим числитель и знаменатель на и находим предел:
.

Пример 4

Все примеры ⇑ Решить предел с помощью ряда Тейлора.
.

Легко видеть, что это неопределенность вида 0/0 . Раскрываем ее, применяя разложения функций в ряд Тейлора. Используем приведенное выше разложение для гиперболического синуса ⇑:
(П4.1) .
В разложении экспоненты, заменим x на –x :
(П4.2) .
Далее, – сложная функция. Сделаем замену переменной . При . Поэтому мы можем используем разложение натурального логарифма в окрестности точки . Используем приведенное выше разложение, в котором переименуем переменную x в t :
(П4.3) .

Заметим, что если бы у нас была функция , то при . Поэтому подставить в предыдущее разложение нельзя, поскольку оно применимо в окрестности точки . В этом случае нам потребовалось бы выполнить следующее преобразование:
.
Тогда при и мы могли бы применить разложение (П4.3).

Попробуем решить предел, выполняя разложение до первой степени переменной x : . То есть оставляем только постоянные члены, не зависящие от x : , и линейные . Остальные будем отбрасывать. Точнее переносить в .
;
;
.
Поскольку , то в разложении логарифма мы отбрасываем члены, начиная со степени 2. Применяя, приведенные выше свойства о малого имеем:

.
Подставляем в предел:

.
Мы снова получили неопределенность вида 0/0 . Значит разложения до степени не достаточно.

Если мы выполним разложение до степени , то опять получим неопределенность:
.

Выполним разложение до степени . То есть будем оставлять только постоянные члены и члены с множителями . Остальные включаем в .
;
;

;

.
Далее замечаем, что . Поэтому в разложении логарифма нужно отбросить члены, начиная со степени , включив их в . Используем разложение (П4.3), заменив t на :

.

Подставляем в исходную функцию.

.
Находим предел.
.

Пример 5

Все примеры ⇑ Найти предел с помощью ряда Тейлора.
.

Будем проводить разложение числителя и знаменателя в ряд Маклорена до четвертой степени включительно.

Теперь переходим к числителю. При . Поэтому сделать подстановку и применить разложение для нельзя, поскольку это разложение применимо при , а у нас . Заметим, что . Поэтому выполним преобразование.
.
Теперь можно сделать подстановку , поскольку при .

Разложим функцию и ее степени в ряд Тейлора в окрестности точки . Применяем приведенное выше разложение ⇑.
;
;

;
;
;
;
Далее заметим, что . Поэтому, чтобы получить разложение сложной функции с точностью до , нам нужно разложить с точностью до .

Разложим второй логарифм. Приводим его к виду , где при .
,
где .

Разложим z в ряд Тейлора в окрестности точки с точностью до .
Применим разложение синуса ⇑:
.
Заменим x на :
. Тогда
;

;
Заметим, что . Поэтому, чтобы получить разложение сложной функции с точностью до , нам нужно разложить с точностью до .

Раскладываем с точностью до и учитываем, что .

;
.

Подставляем разложение числителя и знаменателя и находим предел.
;
.

Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.

Автор: Олег Одинцов . Опубликовано: 29-04-2019

Источник

Как найти частное решение ДУ приближённо с помощью ряда?

Продолжая изучать практические приложения теории рядов, рассмотрим ещё одну распространённую задачу, название которой вы видите в заголовке. И, чтобы не чувствовать себя газонокосилкой на протяжении урока, давайте сразу же разберёмся в сути задания. Три вопроса и три ответа:

Что нужно найти? Частное решение дифференциального уравнения. Намёк между строк шепчет, что к данному моменту желательно хотя бы понимать, что такое дифференциальное уравнение и что такое его решение.

КАК по условию требуется это решение? Приближённо – с помощью ряда.

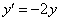
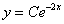
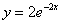
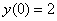
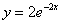
И третий закономерный вопрос: почему приближённо? Этот вопрос я уже освещал на уроке Методы Эйлера и Рунге-Кутты, однако повторение не помешает. Будучи сторонником конкретики, вернусь к простейшему дифференциальному уравнению . В ходе первой лекции по диффурам мы нашли его общее решение (множество экспонент) и частное решение , соответствующее начальному условию . График функции – это самая обычная линия, которую нетрудно изобразить на чертеже.

Но то элементарный случай. На практике встречается великое множество дифференциальных уравнений, неразрешимых аналитически точно (по крайне мере, известными на сегодняшний день способами). Иными словами, как ни крути такое уравнение – проинтегрировать его не удастся. А закавыка состоит в том, что общее решение (семейство линий на плоскости) может существовать. И тогда на помощь приходят методы вычислительной математики.

Встречаем нашу радость!

Типовая задача формулируется следующим образом:

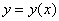
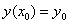
Найти приближённо частное решение дифференциального уравнения …, удовлетворяющее начальному условию , в виде трёх (реже – четырёх-пяти) отличных от нуля членов ряда Тейлора.

Искомое частное решение 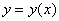раскладывается в данный ряд по известной формуле:

Единственное, здесь вместо буквы «эф» используется «игрек» (так уж повелось).

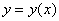
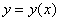
Идея и смысл тоже знакомы: для некоторых диффуров и при некоторых условиях (не будем вдаваться в теорию) построенный степенной ряд будет сходиться к искомому частному решению . То есть, чем больше членов ряда мы рассмотрим, тем точнее график соответствующего многочлена приблизит график функции .

Следует отметить, что вышесказанное применимо и к самым простым случаям. Проведём незамысловатое детское исследование на том же горшке:

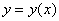
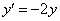
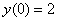
Найти приближённо частное решение дифференциального уравнения , удовлетворяющее начальному условию в виде четырёх первых отличных от нуля членов ряда Тейлора.

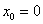
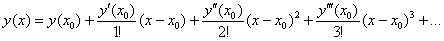
Решение: в условиях данной задачи , поэтому общая формула Тейлора трансформируется в частный случай разложения в ряд Маклорена:

Немного забегая вперёд, скажу, что в практических заданиях значительно чаще встречается именно этот, более компактный ряд.

Занесите обе рабочие формулы в свой справочник.

Разбираемся со значениями 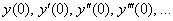. Этапы решения удобно занумеровать:

0) На нулевом шаге записываем значение 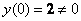, которое всегда известно из условия. В тетради итоговые результаты пунктов желательно обводить в кружок, чтобы они были хорошо видны и не затерялись в решении. Мне по техническим причинам сподручнее выделять их жирным шрифтом. Кроме того, отмечаем, что данное значение не равно нулю! Ведь по условию требуется найти четыре отличных от нуля членов ряда.

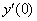
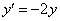
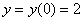
1) Вычислим . Для этого в правую часть исходного уравнения вместо «игрека» подставляем известное значение :

2) Вычислим 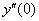. Сначала находим вторую производную:

Подставляем в правую часть найдённое в предыдущем пункте значение :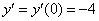

В распоряжении уже три ненулевых члена разложения, нужен ещё один:

3) Находим третью производную – это производная от второй производной:

Так получается, что в данном задании каждая следующая производная оказывается выраженной через предыдущую производную.

Подставляем в правую часть найденное в предыдущем пункте значение :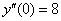

Теперь подставим найденные значения в формулу Маклорена и аккуратно проведём упрощения:

Ответ:

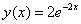
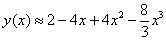
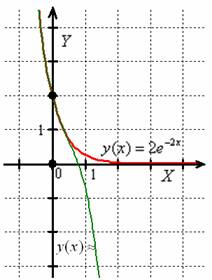
Условие рассматриваемого задания, как правило, не требует чертежа, но я построю демонстрационные графики, чтобы наглядно разъяснить сущность выполненных действий. Изобразим точное частное решение и его приближение :

Как видите, уже 4 члена ряда дают недурственную точность – на довольно длинном участке зелёная дуга кубической функции практически совпала с идеальным («красным») решением, о чём нам сигнализирует коричневый цвет. При этом оба графика проходят через точку начального условия, и естественно, что вблизи неё точность будет максимальной.

Очевидно, что чем больше членов ряда мы рассмотрим, тем лучше соответствующий многочлен приблизит экспоненту.

Неудивительно, что в решении часто задействованы производные более высоких порядков. Кратко повторим материал:

четвёртая производная 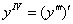– это производная от третьей производной;
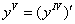
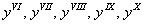
пятая производная – это производная от четвёртой производной и т.д.;
– обозначения 6-й, 7-й, 8-й, 9-й и 10-й производных соответственно.

Помимо римских цифр, в широком обиходе и такой вариант:
– обязательно со скобками, чтобы не путать производную с «игреком в степени».

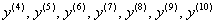
В собственной практике приходилось находить 10-ю производную, не случайно я так подробно воспроизвёл обозначения.

Для успешного выполнения данной задачи необходимо уметь дифференцировать неявную функцию, причём дифференцировать достаточно уверенно. И, прежде чем перейти к конкретным примерам, пожалуйста, проанализируйте, понятны ли вам следующие производные:

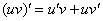
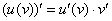
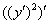
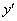
Если не очень, то лучше проработать примеры урока о производных неявно заданных функций. Также проблема может быть в позабытых правилах дифференцирования. В частности, только что и далее будут широко применяться правило дифференцирования произведения и правило дифференцирования сложной функции Пожалуй, некоторая новизна лишь в производной (вторая строка), где в качестве внешней функции выступает степень (квадрат), а в качестве вложения – производная .

Алгоритм и технику решения начнём оттачивать с общего случая разложения в ряд Тейлора:

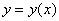
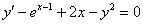
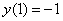
Найти приближённо частное решение дифференциального уравнения , удовлетворяющее начальному условию в виде трёх первых отличных от нуля членов ряда Тейлора.

Решение начинается стандартной фразой:

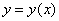
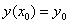
Разложение частного решения дифференциального уравнения при начальном условии имеет вид:

В данной задаче 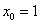, следовательно:

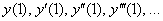
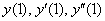
Теперь последовательно находим значения – до тех пор, пока не будут получены три ненулевых результата. Если повезёт, то отличны от нуля будут – это идеальный случай с минимальным количеством работы.

Нарезаем пункты решения:

0) По условию 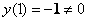. Вот и первый успех.

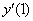
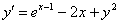
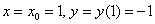
1) Вычислим . Сначала разрешим исходное уравнение относительно первой производной, то есть, выразим . Подставим в правую часть известные значения :

Получена баранка и это не есть хорошо, поскольку нас интересуют ненулевые значения. Однако ноль – тоже результат, который не забываем обвести в кружок или выделить каким-нибудь другим способом.

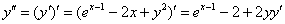
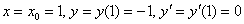
2) Находим вторую производную и подставляем в правую часть известные значения :

3) Находим 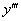– производную от второй производной:

Если действия не понятны, ещё раз призываю изучить статью о дифференцировании неявной функции.

Вообще, задание чем-то напоминает Сказку про Репку, когда дедка, бабка и внучка зовут на помощь жучку, кошку и т.д. И в самом деле, каждая следующая производная выражается через своих «предшественников».

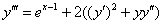
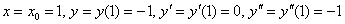
Подставим в правую часть известные значения :

Третье ненулевое значение. Вытащили Репку.

Аккуратно и внимательно подставляем «жирные» числа в нашу формулу:

Ответ: искомое приближенное разложение частного решения:

В рассмотренном примере попался всего один ноль на втором месте, и это не так уж плохо. В общем случае нулей может встретиться сколько угодно и где угодно. Повторюсь, их очень важно выделять наряду с ненулевыми результатами, чтобы не запутаться в подстановках на завершающем этапе.

Вот, пожалуйста – бублик на самом первом месте:

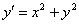
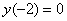
Найти приближённо частное решение дифференциального уравнения , соответствующее начальному условию , в виде трёх первых отличных от нуля членов ряда Тейлора.

Примерный образец оформления задачи в конце урока. Пункты алгоритма можно и не нумеровать (оставляя, например, пустые строки между шагами), но начинающим рекомендую придерживаться строгого шаблона.

Рассматриваемая задача требует повышенного внимания – если допустить ошибку на каком-либо шаге, то всё остальное тоже будет неверным! Поэтому ваша ясная голова должна работать как часы. Увы, это не интегралы или диффуры, которые надёжно решаются и в утомлённом состоянии, поскольку позволяют выполнить эффективную проверку.

На практике заметно чаще встречается разложение в ряд Маклорена:

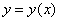
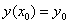
Представить приближенно частное решение ДУ, соответствующее заданному начальному условию , в виде суммы трех первых отличных от нуля членов степенного ряда.

Решение: в принципе, можно сразу записать разложение Маклорена, но оформление задачи академичнее начать с общего случая:

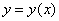
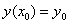
Разложение частного решения дифференциального уравнения при начальном условии имеет вид:

В данном случае 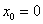, следовательно:

0) По условию .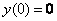

Ну что поделать…. Будем надеяться, что нулей встретится поменьше.

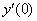
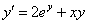
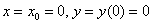
1) Вычислим . Первая производная уже готова к употреблению. Подставим значения :

2) Найдём вторую производную:

И подставим в неё :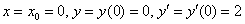

Резво дело пошло!

3) Находим 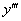. Распишу очень подробно:

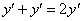
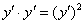
Заметьте, что к производным применимы обычные алгебраические правила: приведение подобных слагаемых на последнем шаге и запись произведения в виде степени: (там же).

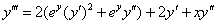
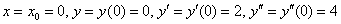
Подставим в всё, что нажито непосильным трудом :

Три ненулевых значения рождены.

Подставляем «жирные» числа в формулу Маклорена, получая тем самым приближенное разложение частного решения:

Ответ:

Для самостоятельного решения:

Представить приближенно частное решение 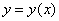ДУ, соответствующее заданному начальному условию , в виде суммы трех первых отличных от нуля членов степенного ряда.

Примерный образец оформления в конце урока.

Как видите, задача с частным разложением в ряд Маклорена оказалась даже труднее общего случая. Сложность рассматриваемого задания, как мы только что убедились, состоит не столько в самом разложении, сколько в трудностях дифференцирования. Более того, порой, приходится находить 5-6 производных (а то и больше), что повышает риск ошибки. И в завершении урока предлагаю пару задач повышенной сложности:

Решить дифференциальное уравнение приближённо с помощью разложения частного решения в ряд Маклорена, ограничившись тремя первыми ненулевыми членами ряда

Решение: перед нами диффур второго порядка, но это практически не меняет дела. По условию 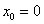и нам сразу же предложено воспользоваться рядом Маклорена, чем мы не преминем воспользоваться. Запишем знакомое разложение, прихватив на всякий пожарный побольше слагаемых:

Алгоритм работает точно так же:

0) – по условию.

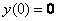
1) – по условию.

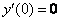
2) Разрешим исходное уравнение относительно второй производной: .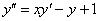

И подставим :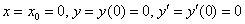

Первое ненулевое значение

Щёлкаем производные и выполняем подстановки:

3)

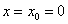
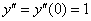
Подставим и :

4)

Подставим :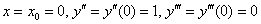

Второе ненулевое значение.

5) – по ходу дел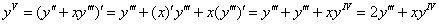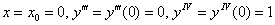а приводим подобные производные.

Подставим :

6)

Подставим :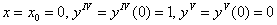

Наконец-то. Впрочем, бывает и хуже.

Таким образом, приближенное разложение искомого частного решения:

Ответ:

Миниатюра для самостоятельного решения:

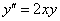
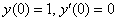
Найти три отличных от нуля члена разложения в ряд Маклорена частного решения дифференциального уравнения второго порядка при начальных условиях .

Я хочу, чтобы все читатели решили это задание. Ведь курс математического анализа потихоньку заканчивается…. пройдут годы, но когда-нибудь каждого из вас посетит непреодолимое желание что-нибудь продифференцировать. Поэтому не упускайте редкую возможность начать прямо сейчас =)

Решения и ответы:

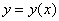
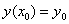
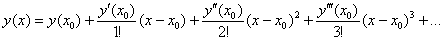
Пример 3: Решение: разложение частного решения ДУ при начальном условии имеет вид: .
В данном случае: .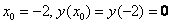
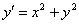
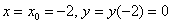
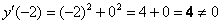
В правую часть подставим :

Найдём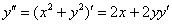
Подставим :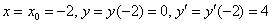

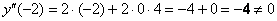
Найдём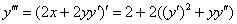
Подставим :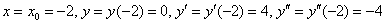

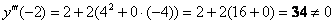
Таким образом, искомое приближенное разложение частного решения: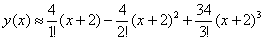

Ответ:

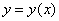
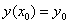
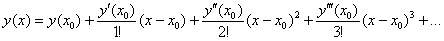
Пример 5: Решение: разложение частного решения ДУ при начальном условии имеет вид: .
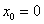
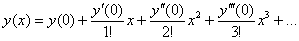
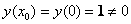
В данном случае , следовательно:

.
Разрешим исходное уравнение относительно .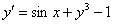
Подставим :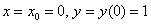

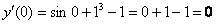
Найдём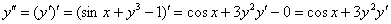
Подставим :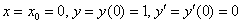

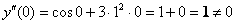
Найдём третью производную: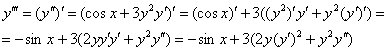

Подставим :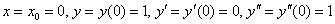

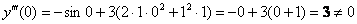
Таким образом, искомое приближенное разложение частного решения: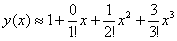

Ответ:

Пример 7: Решение: используем разложение Маклорена: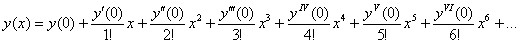

По условию:

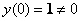
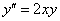
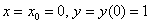
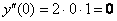
В исходное уравнение подставим :

Найдём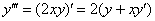
Подставим :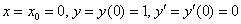

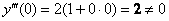
Найдём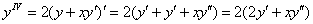
Подставим :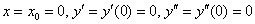

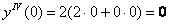
Найдём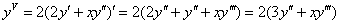
Подставим :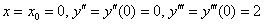

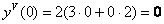
Найдём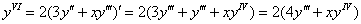
Подставим :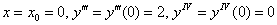

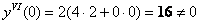
Таким образом, приближенное разложение искомого частного решения: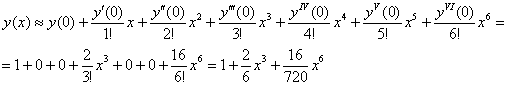

Ответ:

Автор: Емелин Александр

(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Источник