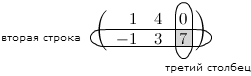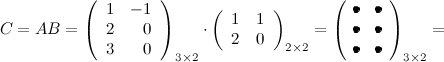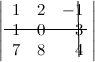Задачи по матрицам способы

Примеры решения задач с матрицами

Матрицы широко применяются в математике для компактной записи СЛАУ или систем дифференциальных уравнений. Тогда количество строк матрицы соответствует количеству уравнений системы, а количество столбцов равно количеству неизвестных. Матричный аппарат позволяет свести решение громоздких СЛАУ к компактным операциям над матрицами.

На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию матриц и научиться решать задачи с ними. Перед изучением примеров решения задач советуем изучить теоретический материал по матрицам, прочитать все определения и свойства. Список тем находится в правом меню.

Примеры по темам:

Матрицы: основные определения и понятия

Задание. Чему равен элемент $ a_ <23>$ матрицы $ A=\left( \begin <1>& <4>& <0>\\ <-1>& <3>& <7>\end\right) $ ?

Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:

Таким образом, $a_<23>=7$.

Ответ. $a_<23>=7$

Умножение матрицы на число

Теоретический материал по теме — умножение матрицы на число.

Примеры решения задач с матрицами не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Пусть $A=\left( \begin <3>\\ <-1>\end\right)$ . Найти матрицу 2$A$.

Ответ. $2 A=\left( \begin <6>\\ <-2>\end\right)$

Сложение и вычитание матриц

Теоретический материал по теме — сложение и вычитание матриц.

Задание. Найти матрицу $C=A-3 B$, если $A=\left( \begin <1>& <2>\\ <2>& <-1>\\ <3>& <0>\end\right), B=\left( \begin <-1>& <1>\\ <1>& <2>\\ <0>& <0>\end\right)$

Умножение матриц

Теоретический материал по теме — умножение матриц.

Задание. Вычислить $A B$ и $B A$, если $A=\left( \begin <1>& <-1>\\ <2>& <0>\\ <3>& <0>\end\right), B=\left( \begin <1>& <1>\\ <2>& <0>\end\right)$

Решение. Так как $A=A_<3 \times 2>$ , а $B=B_<2 \times 2>$ , то произведение возможно и результатом операции умножения будет матрица $C=C_<3 \times 2>$ , а это матрица вида $C=\left( \begin> & > \\ > & > \\ > & >\end\right)$ .

Вычисли элементы матрицы $C$ :

$ c_<11>=a_ <11>\cdot b_<11>+a_ <12>\cdot b_<21>=1 \cdot 1+(-1) \cdot 2=-1 $

$ c_<12>=a_ <11>\cdot b_<12>+a_ <12>\cdot b_<22>=1 \cdot 1+(-1) \cdot 0=1 $

$ c_<21>=a_ <21>\cdot b_<11>+a_ <22>\cdot b_<21>=2 \cdot 1+0 \cdot 2=2 $

$ c_<22>=a_ <21>\cdot b_<12>+a_ <22>\cdot b_<22>=2 \cdot 1+0 \cdot 0=2 $

$ c_<31>=a_ <31>\cdot b_<11>+a_ <32>\cdot b_<21>=3 \cdot 1+0 \cdot 2=3 $

$ c_<31>=a_ <31>\cdot b_<12>+a_ <32>\cdot b_<22>=3 \cdot 1+0 \cdot 0=3 $

Выполним произведения в более компактном виде:

Найдем теперь произведение $D=B A=B_ <2 \times 2>\cdot A_<3 \times 2>$. Так как количество столбцов матрицы $B$ (первый сомножитель) не совпадает с количеством строк матрицы $A$ (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.

Ответ. $A B=\left( \begin <-1>& <1>\\ <2>& <2>\\ <3>& <3>\end\right)$ . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы $B$ не совпадает с количеством строк матрицы $A$ .

Транспонирование матрицы

Теоретический материал по теме — транспонирование матрицы.

Задание. Найти матрицу $A^$, если $A=\left( \begin <1>& <0>\\ <-2>& <3>\end\right)$

Минор и алгебраическое дополнение

Задание. Найти минор $M_<23>$ к элементу $a_<23>$ определителя $\left| \begin <1>& <2>& <-1>\\ <1>& <0>& <3>\\ <7>& <8>& <4>\end\right|$ .

Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:

Задание. Найти алгебраическое дополнение $A_<23>$ к элементу $a_<23>$ определителя $\left| \begin <1>& <2>& <-1>\\ <1>& <0>& <3>\\ <7>& <8>& <4>\end\right|$ .

Вычисление определителя

Задание. Вычислить определитель второго порядка $\left| \begin <11>& <-2>\\ <7>& <5>\end\right|$

Решение. $\left| \begin <11>& <-2>\\ <7>& <5>\end\right|=11 \cdot 5-(-2) \cdot 7=55+14=69$

Задание. Вычислить определитель $\left| \begin <3>& <3>& <-1>\\ <4>& <1>& <3>\\ <1>& <-2>& <-2>\end\right|$ методом треугольников.

Решение. $\left| \begin <3>& <3>& <-1>\\ <4>& <1>& <3>\\ <1>& <-2>& <-2>\end\right|=3 \cdot 1 \cdot(-2)+4 \cdot(-2) \cdot(-1)+$

$+3 \cdot 3 \cdot 1-(-1) \cdot 1 \cdot 1-3 \cdot(-2) \cdot 3-4 \cdot 3 \cdot(-2)=54$

Задание. Вычислить определитель $\left| \begin <1>& <2>& <3>\\ <4>& <5>& <6>\\ <7>& <8>& <9>\end\right|$

Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.

Определитель равен нулю, так как вторая и третья строки являются пропорциональными.

Задание. Вычислить определитель $\Delta=\left| \begin <-2>& <1>& <3>& <2>\\ <3>& <0>& <-1>& <2>\\ <-5>& <2>& <3>& <0>\\ <4>& <-1>& <2>& <-3>\end\right|$ приведением его к треугольному виду.

Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент $a_<11>$ будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:

Далее получим нули в первом столбце, кроме элемента $a_<11>$ , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:

Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен $\pm 1$ , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):

Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:

Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:

Ответ. $\Delta=-80$

Нахождение обратной матрицы

Задание. Для матрицы $A=\left( \begin <7>& <4>\\ <5>& <3>\end\right)$ найти обратную методом присоединенной матрицы.

Решение. Приписываем к заданной матрице $A$ справа единичную матрицу второго порядка:

От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):

От второй строки отнимаем две первых:

Первую и вторую строки меняем местами:

От второй строки отнимаем две первых:

Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:

Итак, слева получили единичную матрицу, а значит матрица, стоящая в правой части (справа от вертикальной черты), является обратной к исходной.

Таким образом, получаем, что $A^<-1>=\left( \begin <3>& <-4>\\ <-5>& <7>\end\right)$

Задание. Найти обратную матрицу для $A=\left( \begin <1>& <1>\\ <1>& <2>\end\right)$

Решение. Шаг 1. Находим определитель: $\Delta=\left| \begin <1>& <1>\\ <1>& <2>\end\right|=2-1=1 \neq 0$

Задание. Найти обратную матрицу к матрице $A=\left( \begin <1>& <0>& <2>\\ <2>& <-1>& <1>\\ <1>& <3>& <-1>\end\right)$

Решение. Вычисляем определитель матрицы:

$\Delta=\left| \begin <1>& <0>& <2>\\ <2>& <-1>& <1>\\ <1>& <3>& <-1>\end\right|=1 \cdot(-1) \cdot(-1)+2 \cdot 3 \cdot 2+0 \cdot 1 \cdot 1-$

$-1 \cdot(-1) \cdot 2-3 \cdot 1 \cdot 1-2 \cdot 0 \cdot(-1)=1+12+0+2-3+0=12 \neq 0$

Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица $A^<-1>$ к матрице $A$ находится по формуле:

Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):

Нахождение ранга матрицы

Теоретический материал по теме — нахождение ранга матрицы.

Решение. С помощью элементарных преобразований над ее строками приведем матрицу $A$ к ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:

От второй строки отнимаем четвертую строку, умноженную на 4; от третьей — две четвертых:

Ко второй строке прибавим пять первых, к третьей — три третьих:

Меняем местами первую и вторую строчки:

Далее четвертую и первую строки:

Ответ. $\operatorname A=2$

Задание. Найти ранг матрицы $A=\left( \begin <1>& <2>& <-1>& <-2>\\ <2>& <4>& <3>& <0>\\ <-1>& <-2>& <6>& <6>\end\right)$ , используя метод окаймления миноров.

Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам матрицы $A$ . Рассмотрим, например, минор $M_<1>=1 \neq 0$ . расположенный в первой строке и первом столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор $M_<2>^<1>=\left| \begin <1>& <2>\\ <2>& <4>\end\right|=0$ ; рассмотрим еще один минор второго порядка, для этого минор $M_<1>$ окаймляем при помощи второй строки и третьего столбца, тогда имеем минор $M_<2>^<2>=\left| \begin <1>& <-1>\\ <2>& <3>\end\right|=5 \neq 0$ , то есть ранг матрицы не меньше двух. Далее рассматриваем миноры третьего порядка, которые окаймляют минор $M_<2>^<2>$ . Таких миноров два: комбинация третьей строки со вторым столбцом или с четвертым столбцом. Вычисляем эти миноры:

так как содержит два пропорциональных столбца (первый и второй); второй минор

преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:

И так как первая и вторая строки пропорциональны, то минор равен нулю.

Таким образом, все окаймляющие миноры третьего порядка равны нулю. А, значит, ранг матрицы $A$ равен двум: $\operatorname A=2$

Ответ. $\operatorname A=2$

Источник

Матрицы: примеры с решением и объяснением

Вы будете перенаправлены на Автор24

Матрицы представляют собой таблицы чисел, взаимосвязанных между собой. Над ними возможно проводить ряд разнообразных операций, о которых мы расскажем вам ниже.

Размер матрицы определяется её порядками — количеством строчек $m$ и столбцов $n$, которые в ней присутствуют. Строчки образованы элементами, стоящими на горизонтальных линиях, а столбцы — элементами, стоящими на прямых вертикальных линиях. В случае если количество строчек эквивалентно количеству столбцов — порядок рассматриваемой таблички определяется лишь одним значением $m = n$.

Для любого элемента матрицы номер строчки, в которой он находится, записывается первым в индексе, а номер столбца — вторым, то есть запись $a_$ обозначает, что элемент стоит в $i$-ой строчке и в $j$-ом столбце.

Сложение и вычитание

Итак, о сложении и вычитании. Эти действия возможно проводить только с матрицами одинакового размера.

Для того чтобы осуществить эти действия, необходимо провести сложение или вычитание каждого элемента матрицы с элементом другой матрицы, стоящим на той же позиции, что элемент в первой.

В качестве примера найдём сумму $A+B$, где:

Сумма любого элемента новой полученной матричной таблички $A + B$ равна $a_ + b_$, например, элемент с индексом $11$ равен $a_ <11>+ b_<11>$,а весь результат целиком выглядит так:

Вычитание для двух матриц $A-B$ осуществляется аналогично, но каждый элемент новой матрицы результата будет вычисляться по формуле $a_ – b_$.

Готовые работы на аналогичную тему

Обратите внимание, что сложение и вычитание для матриц возможно осуществлять только если их порядки одинаковые.

Решите следующие матричные примеры: $A + B$; $A – B$.

$A=\begin 0 & 5 & 2 \\ 1 & -1 & 3 \\ -2 & 0 & 7 \\ \end$

$B=\begin 0 & 3 & 2 \\ -4 & 0 & -1 \\ 0 & 7 & -3 \\ \end$

Объяснение:

Действия выполняем для каждой пары элементов $a_$ и $b_$ соответственно:

$A+B=\begin 0+0 & 5+3 & 2+2 \\ 1-4 & -1+0 & 3 — 1\\ -2+0 & 0+7 & 7 — 3 \\ \end=\begin 0 & 8 & 4 \\ -3 & -1 & 2 \\ -2 & 7 & 4\\ \end$

$A-B=\begin 0-0 & 5-3 & 2-2 \\ 1+4 & -1-0 & 3 + 1\\ -2-0 & 0-7 & 7 + 3 \\ \end=\begin 0 & 2 & 0 \\ 5 & -1 & 4 \\ -2 & -7 & 10 \\ \end$

Умножение матрицы на число

Для того чтобы произвести умножение матричной таблички на какое-либо число, нужно каждый её элемент умножить на это число, то есть любой элемент новой матрицы $C$, являющейся результатом произведения $A$ на $λ$ будет равен $с_=λ \cdot a_$.

Умножьте $A$ на $λ$, где $A=\begin 1 & 0 & 2 \\ -1 & 3 & 0 \\ 2 & 1 & 3 \\ \end$, а $λ=5$:

$A \cdot λ = 5 \cdot \begin 1 & 0 & 2 \\ -1 & 3 & 0 \\ 2 & 1 & 3 \\ \end = \begin 1 \cdot 5 & 0 \cdot 5 & 2 \cdot 5 \\ -1 \cdot 5 & 3 \cdot 5 & 0 \cdot 5 \\ 2 \cdot 5 & 1\cdot 5 & 3\cdot 5 \\ \end = \begin 5 & 0 & 10 \\ -5 & 15 & 0 \\ 10 & 5 & 15 \\ \end$.

Произведение матричных таблиц

Эта задача несколько сложнее предыдущих, но при этом в ней также нет ничего сложного.

Для осуществления умножения двух матриц $A \cdot B$ количество столбцов в $A$ должно совпадать с количеством строчек в $B$.

Математически это можно записать так:

То есть видя перемножаемые исходные матрицы можно сразу определить порядки получаемой новой. Например, если необходимо перемножить $A_<3 \times 2>$ и $B_<2 \times 3>$ — полученный результат будет иметь размер $3 \times 3$:

Если число столбцов первого матричного множителя не совпадает с количеством строчек второго матричного множителя, то умножение выполнить невозможно.

$A \times B = ?$, если $A=\begin 1 & 0 & 2 \\ -1 & 3 & 0 \\ 2 & 1 & 3 \\ \end$ и $B = \begin 3 & — 1 & 2 \\ -4 & 0 & 2 \\ 1 & 1 & 2 \\ \end$.

$A \times B = \begin (1 \cdot 3 + 0 \cdot (-4) + 2 \cdot 1) & (1 \cdot(-1) + 0 \cdot 0 + 2 \cdot 1) & (1 \cdot 2 + 0 \cdot 2 + 2 \cdot 2) \\ (-1) \cdot 3 + 3 \cdot (-4) + 0 \cdot 1) & (-1 \cdot(-1) + 3 \cdot 0 + 0 \cdot 1) & (-1 \cdot 2 + 3 \cdot 2 + 0 \cdot 2) \\ (2 \cdot 3 + 1 \cdot (-4) + 3 \cdot 1) & 2 \cdot (-1) + 1 \cdot 0 + 3 \cdot 1) & (2 \cdot 2 + 1 \cdot 2 + 3 \cdot 2) \\ \end $

$A \times B= \begin (3 + 0+ 2) & (-1 + 0 + 2) & (2 + 0 + 4) \\ (-3-12+0) & (1 + 0 + 0) & (-2+6+0) \\ (6-4+3) & (-2 + 0 + 3) & (4 + 2 + 6) \\ \end = \begin 5 & 1 & 6 \\ -15 & 1 & 4 \\ 5 & 1 & 12 \\ \end$.

Нахождение определителя матрицы

Определитель матрицы обозначается как $Δ$ или $\det$.

Детерминант возможно найти только для квадратных разновидностей матриц.

В простейшем случае, когда матрица состоит из всего одного элемента, её определитель равен этому элементу: $det A = |a_<11>|= a_<11>$

Вычислить определитель от матрицы порядка двух можно следуя такому правилу:

Определитель матрицы размера 2 равен разности произведений элементов, стоящих на главной диагонали с произведением элементов с побочной диагонали:

В случае если определитель матрицы задан размером $3 \times 3$, то найти его можно используя мнемонические правила: Саррюса или треугольников, также можно разложить матрицу по строчке или столбцу или воспользоваться преобразованиями Гаусса.

Для определителей большего размера можно использовать преобразования Гаусса и разложение по строчке.

Обратные матрицы

По аналогии с обычным умножением числа на обратное ему число $(1+\frac1x= 1)$, умножение обратной матрицы $A^<-1>$ на исходную матрицу даёт в результате единичную матрицу $E$.

Самый простой метод решения при поиске обратной матрицы — Жордана-Гаусса. Рядом с матрицей-подопытным кроликом записывается единичная того же размера, а затем исходная с помощью преобразований приводится к единичной, причём все выполняемые действия повторяются и с $E$.

Получить обратную матрицу.

Решение:

Пишем вместе $A$ и справа от неё соответствующего размера $E$:

$ \begin 1& 2 & 1& 0\\ 3 & 4& 0 & 1 \\ \end$

Получаем нуль в последней строчке на первой позиции:прибавляем к ней верхнюю, умноженную на $-3$:

$ \begin 1& 2 & 1 & 0\\ 0 & -2 & -3 & 1 \\ \end$

Теперь обнуляем последний элемент первой строчки. Для этого к верхней строчке плюсуем нижнюю:

$ \begin 1& 0 & -2 & 1\\ 0 & -2 & -3 & 1 \\ \end$

Делим вторую на $-2$:

$ \begin 1& 0 & -2 & 1\\ 0 & 1& 3/2 & -1/2 \\ \end$

Транспонирование матричных таблиц

Транспонирование — это смена строк и столбцов в матрице или определителе местами с сохранением их исходного порядка. Определитель траспонированной матричной таблички $A^T$ будет равен определителю исходной матрицы $A$.

Транспонируйте матрицу $A$ и проверьте себя, найдя определитель $A$ и транспонированной матричной таблички.

$A=\begin 1 & 2 & 3 \\ 4 & 5 & 6 \\ — 1 & -2 & -3\\ \end$

Решение:

Применим метод Саррюса для детерминанта:

$\det A= 1 \cdot 5 \cdot (-3) + 2 \cdot 6 \cdot (-1) + 3 \cdot 4 \cdot (-2) – 2 \cdot 4 \cdot (-3) – 1 \cdot 6 \cdot (-2) – 3 \cdot 5 \cdot (-1) = -15 – 12 – 24+ 24 + 12 + 15 = 0$.

Мы получили вырожденную матрицу.

Теперь произведём транспонирование $A$, для этого повалим матрицу на её правый бок:

$A^T = \begin 1 & 4 & -1 \\ 2 & 5 & -2 \\ 3 & 6 & -3 \\ \end$

Найдём для $A^T$ определитель, используя то же правило:

$det A^T = 1 \cdot 5 \cdot (-3) + 4 \cdot (-2) \cdot 3 + (-1) \cdot 2 \cdot 6 – 4 \cdot 2 \cdot (-3) – 1 \cdot (-2) \cdot 6 – (- 1) \cdot 5 \cdot 3 = — 15 -24 — 12+24+12+15 = 0$.

Источник