Сервис для решения задач по линейному программированию

и другие интересные типовые задачи English

Пример №2. Решение задачи линейного программирования графическим методом.
Функция достигает наименьшего значения в точке

при следующих ограничениях:

	x1	+	2 x2	≤	8
	x1	—	x2	≤	2
	x1	+	2 x2	≥	4
	x1	≥	1

x₁ ≥ 0 x₂ ≥ 0

Точки, координаты которых удовлетворяют одновременно всем неравенствам системы ограничений, называются областью допустимых решений.

Очевидно, для нахождения области допустимых решений данной задачи, необходимо последовательно рассмотреть каждое неравенство. (см. шаг 1 — шаг 4)

Последние два шага служат непосредственно для получения ответа. (см. шаг 5 — шаг 6)

Это стандартная схема решения. Если область допустимых решений представляет собой точку или пустое множество, то решение будет короче.

По условию задачи: x₁ ≥ 0 x₂ ≥ 0.

Если бы это было единственным условием, то область допустимых решений имела бы вид, как на рисунке (вся первая четверть).

Рассмотрим неравенство 1 системы ограничений.

Построим прямую: x₁ + 2 x₂ = 8

Найдены коородинаты двух точек (0, 4) и (8 ,0). Соединяем их и получаем необходимую прямую (1).

Нас интересуют точки расположенные выше или ниже построенной прямой (1) ?
Вернемся к исходному неравенству.

Преобразуем неравенство, оставив в левой части только x₂

Знак неравенства ≤ . Следовательно, нас интересуют точки расположенные ниже построенной прямой (1).

Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.

Рассмотрим неравенство 2 системы ограничений.

Найдены коородинаты двух точек (0, -2) и (2 ,0). Соединяем их и получаем необходимую прямую (2).

Нас интересуют точки расположенные выше или ниже построенной прямой (2) ?
Вернемся к исходному неравенству.

Преобразуем неравенство, оставив в левой части только x₂

Знак неравенства ≥ . Следовательно, нас интересуют точки расположенные выше построенной прямой (2).

Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.

Рассмотрим неравенство 3 системы ограничений.

Построим прямую: x₁ + 2 x₂ = 4

Найдены коородинаты двух точек (0, 2) и (4 ,0). Соединяем их и получаем необходимую прямую (3).

Нас интересуют точки расположенные выше или ниже построенной прямой (3) ?
Вернемся к исходному неравенству.

Преобразуем неравенство, оставив в левой части только x₂

Знак неравенства ≥ . Следовательно, нас интересуют точки расположенные выше построенной прямой (3).

Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.

Рассмотрим неравенство 4 системы ограничений.

Построим прямую: x₁ = 1

Данная прямая параллельна оси OX₂ и проходит через точку (1,0) (4)

Знак неравенства ≥ . Следовательно, нас интересуют точки расположенные правее построенной прямой (4).

Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.

Строим вектор C = (2, 2), координатами которого являются коэффициенты функции F.

Будем перемещать «красную» прямую, перпендикулярно вектору C , от левого нижнего угла к правому верхнему.

В точке, в которой «красная» прямая в первый раз пересечет область допустимых решений, функция F достигает своего наименьшего значения.

В точке, в которой «красная» прямая в последний раз пересечет область допустимых решений, функция F достигает своего наибольшего значения.

Функция F достигает наименьшего значения в точке A. (см. рисунок)

Найдем координаты точки A.
Точка A одновременно принадлежит прямым (3) и (4).

	x1	+	2 x2	=	4	=>	x1 = 1
	x1	=	1	x2 = 3/2

Вычислим значение функции F в точке A (1,3/2).

F (A) = 2 * 1 + 2 * 3/2 = 5

x₁ = 1

x₂ = 3/2

F _min = 5

Замечание: если возникли сомнения, что функция F достигает своего минимума в точке А, необходимо найти значение функции в интересующей точке и сравнить с F(A).

Источник

Графический способ решения производственной задачи

Условие

Сначала запишем условие производственной задачи из предыдущей главы:

Ресурс	Изделие A	Изделие B	Сколько ресурса на складах
R1	1	3	15
R2	2	1	20
R3	3	2	35
Прибыль	5	10

У нас получилась система ограничений и целевая функция следующего вида:

Строим область допустимых решений

Чтобы решить данную задачу линейного программирования графическим методом, необходимо сначала превратить (мысленно) все неравенства в равенства, и на время забыть про целевую функцию. То есть, получить следующую систему:

Мы получили пять уравнений с двумя переменными, следовательно, мы можем построить их графики. Например, мы можем направить ось с переменной $x_A$ вправо (где обычно у нас ось абсцисс) и ось с переменной $x_B$ вверх (где обычно у нас ось ординат). Для построения графиков нужно лишь выразить из этих уравнений $x_B$. Сделаем это:

Прежде чем строить графики, разберемся с последними двумя уравнениями, $x_A=0$ и $x_B=0$. Эти уравнения выражают сами оси — абсцисс и ординат. А так как в исходных ограничениях были неравенства $x_A\geq0$ и $x_B\geq0$, то точка нашего решения должна быть правее и выше, чем эти оси — то есть, находиться в первой четверти. Поэтому эти две линии можно не строить, а просто учитывать, что решение в первой четверти.

Остальные линии мы построим на графике, и получим следующую картину (естественно, на нормальном графике не нужно рисовать такие стрелки, они лишь для наглядности, чтобы не перепутать линии друг с другом):

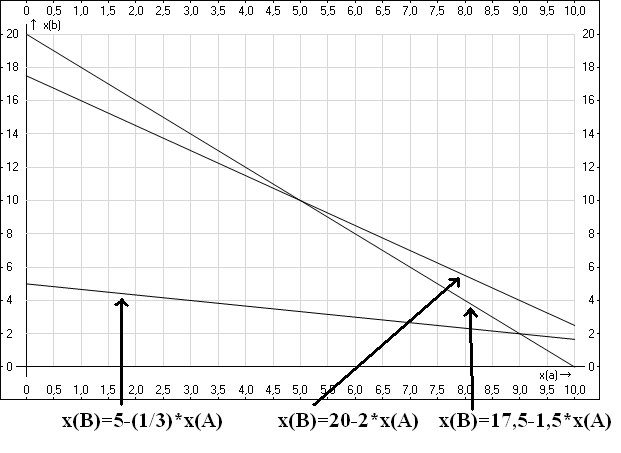
Каждая из этих линий разбивает область допустимых решений на две — одна находится правее и выше каждой из этих линий, вторая — левее и ниже. Какая из них нужна нам? Та, которая левее и ниже. Во-первых, в исходных неравенствах у нас был знак «меньше или равно», а левее и ниже как раз более маленькие значения переменных. А во-вторых, как мы говорили в предыдущем пункте, решение (0,0) вполне удовлетворяет условию задачи, хоть и не является оптимальным. А точка (0,0) — начало координат — расположена как раз левее и ниже каждой из прямых.

То есть, нам нужно найти область, расположенную левее и ниже, чем каждая из наших прямых. Отобразим ее:

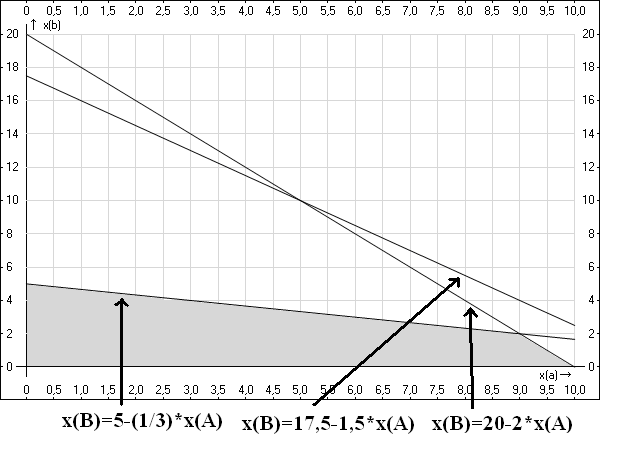
Эта область, во-первых, расположена в первой четверти, как и должно быть, во-вторых, левее и ниже прямых $x_B=5-\frac<1><3>x_A$ и $x_B=20-2x_A$. Прямая $x_B=17,5-1,5x_A$ оказалась не участвующей в решении, так иногда бывает, это не страшно.

Далее задачу можно решать двумя способами.

Основной способ

Рассмотрим первый из них. Для него нужно нарисовать линию нулевого дохода, то есть, линию, при которой целевая функция равна нулю: $5x_A+10x_B=0$. Если упростить данное выражение, получим $x_B=-0,5x_A$. Построим эту функцию красным цветом, и уберем подписи. Она будет расположена не в первой четверти, это нормально.

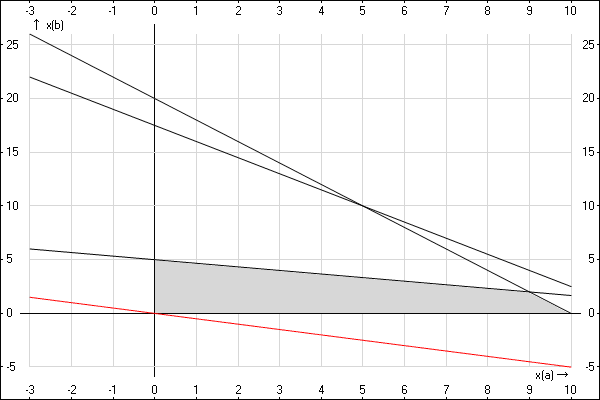
Эта линия состоит из точек, каждая из которых является решением, применяя которое, мы получим нулевой доход. Однако с тем условием, что $x_A,x_B\geq0$, такое решение мы получаем всего одно — в точке (0,0) — остальные точки лежат во второй и четвертой четверти.

Что будет, если эту линию поднимать выше (параллельным переносом)? Мы получим линии, которые будут давать больший, чем 0 доход. Получается, чем выше мы поднимем данную линию, тем лучше. Однако совсем до бесконечности поднимать ее не получится, ведь она должна хотя бы касаться разрешенной области, обозначенной серым цветом (сейчас она касается только в точке (0,0)). Попробуем провести (пока на глаз) линии, параллельные данной, через оставшиеся три точки многоугольника:

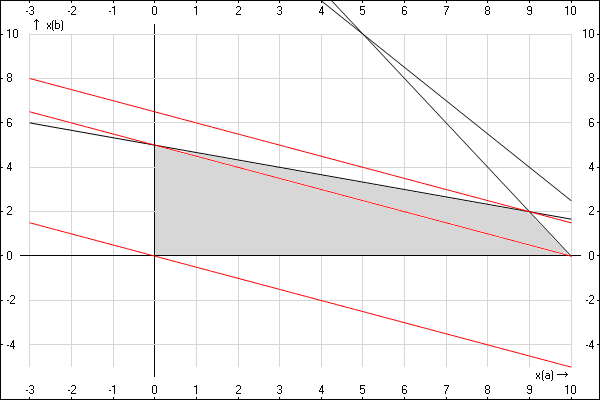
Мы нарисовали еще две линии, параллельные линии нулевого дохода, но расположенные выше. Средняя из них проходит через две точки нашего многоугольника с решениями, а самая высокая — через еще одну точку многоугольника. Кроме того, она вообще пересекает наш многоугольник в одной-единственной точке. И еще выше данную линию поднять нельзя — она вообще перестанет пересекать наш многоугольник. Следовательно, эта линия и есть «линия максимального дохода», а наше решение находится, как раз, в той точке, в которой эта линия пересекает нашу область допустимых решений — в точке пересечения линий $x_B=5-\frac<1><3>x_A$ и $x_B=20-2x_A$. Найдем координаты данной точки. Для этого приравняем эти два значения для $x_B$:

$$5-\frac<1><3>x_A=20-2x_A$$ $$-\frac<1><3>x_A+2x_A=20-5$$ $$\frac<5><3>x_A=15$$ $$5x_A=45$$ $$x_A=9$$ $$x_B=20-2\cdot9=20-18=2$$

Итак, наше решение находится в точке (9,2). Это означает, что необходимо производить 9 единиц изделия A и 2 единицы изделия B. При этом мы получим прибыль

Во всех остальных точках многоугольника решений прибыль будет меньше.

Другой способ

Второй способ заключается в том, что нужно просто проверить значение целевой функции в каждой точке многоугольника. Всего их четыре. Обозначим их буквами:

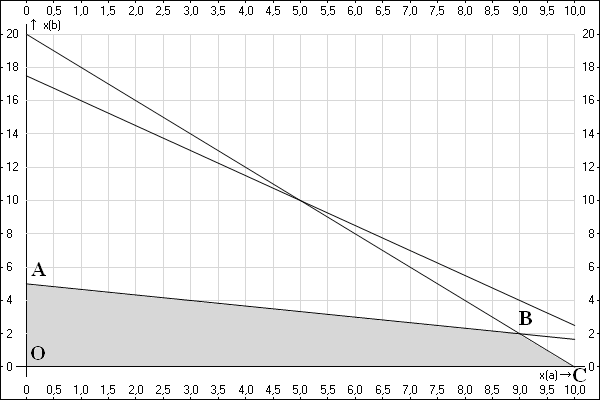
Найдем координаты каждой из них. Координаты точки O мы знаем — (0,0). Координаты точки B мы нашли выше (по первому способу) — (9,2). Точка A — это точка на прямой $x_B=5-\frac<1><3>x_A$, причем $x_A=0$. Следовательно $x_B=5$. То есть, ее координаты (0,5). Точка C — это точка на прямой $x_B=20-2x_A$, причем $x_B=0$. То есть, $20-2x_A=0$, $2x_A=20$, $x_A=10$. Следовательно, ее координаты (10,0).

Теперь найдем значение целевой функции в каждой из данных точек:

$$F(O)=F(0,0)=5\cdot0+10\cdot0=0+0=0$$ $$F(A)=F(0,5)=5\cdot0+10\cdot5=0+50=50$$ $$F(B)=F(9,2)=5\cdot9+10\cdot2=45+20=65$$ $$F(C)=F(10,0)=5\cdot10+10\cdot0=50+0=50$$

Действительно, в точке B наша функция принимает максимальное значение, равное 65. Это и есть максимальная прибыль, которую можно получить в данном случае.

А если товаров больше?

Как говорилось в предыдущем разделе, графическим способом можно решать только задачу для двух производимых товаров. Это потому, что если товаров будет больше двух, то и переменных будет больше двух, например, три — $x_A, x_B, x_C$. И тогда придется строить трехмерный график, в котором запросто можно запутаться. А если переменных больше трех, то график не построить вообще. Однако специально для этих случаев был разработан еще один метод решения задач линейного программирования, и, в частности, производственной задачи — симплекс-метод, который мы рассмотрим в следующей главе.

Источник

Задачи по линейному программированию

Ответы на вопросы по заказу заданий по линейному программированию:

Сколько стоит помощь?

• Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

Какой срок выполнения?

• Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.

Если требуется доработка, это бесплатно?

• Доработка бесплатна. Срок выполнения от 1 до 2 дней.

Могу ли я не платить, если меня не устроит стоимость?

• Оценка стоимости бесплатна.

Каким способом можно оплатить?

• Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

Какие у вас гарантии?

• Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.

В какое время я вам могу написать и прислать задание на выполнение?

• Присылайте в любое время! Я стараюсь быть всегда онлайн.

Содержание:

Линейное программирование

Задача линейного программирования. Каноническая и стандартная формы

Пусть — множество, заданное системой ограничений

где каждый из знаков означает или Предполагается, что система (7.1) содержит неравенства

Пусть также задана линейная функция

Множество называется допустимым, а любая точка — допустимым решением; функция называется целевой функцией. Задача линейного программирования (ЛП) состоит в отыскании наибольшего или наименьшего значения целевой функции (7.3) на множестве допустимых решений. Записывается это следующим образом:

при

Любая точка для которой — наибольшее (наименьшее) значение на называется оптимальным решением.

Если система (7.1) состоит только из уравнений и неравенств вида (7.2), то говорят о канонической форме задачи ЛП, если же в системе (7.1) присутствуют только неравенства, то говорят о стандартной форме задачи ЛП. Если предполагается, что

целые числа, то соответствующая задача называется целочисленной. Любая задача ЛГ1 может быть сведена как к канонической, так и к стандартной форме.

Возможно, вас также заинтересует эта ссылка:

Задача 1.

Стальные прутья длиной 110 см требуется разрезать на заготовки длиной 50, 45, 30 см. Заготовок длиной 50 см должно быть изготовлено не менее 20, длиной 45 см — не менее 40, длиной 30 см не менее 60. Сколько прутьев и каким способом следует разрезать, чтобы получить указанное количество заготовок при минимальных отходах? Составить математическую модель этой задачи.

Нетрудно перебрать все возможные варианты разреза (табл. 7.1):

Пусть — количество прутьев, разрезаемых по варианту с номером Набор натуральных чисел составляет план разреза. Из условий задачи вытекают следующие oipa-ничения на неизвестные

Суммарное количество отходов описывается функцией

В итоге приходим к следующей стандартной задаче ЛП:

при условиях (7.4).

Сформулированную задачу можно привести к канонической форме. Это достигается введением дополнительных (балансовых) переменных

Возможно, вас также заинтересует эта ссылка:

Задача 2.

На двух складах имеется 50 и 100 тонн товара соответственно. Потребности магазинов в товаре соответственно равны 30, 40, 80 тонн. Известны тарифы перевозок , где — стоимость в рублях перевозки одной тонны товара со склада в магазин Найти минимальный по стоимости план перевозки товара со складов в магазины. Составить математическую модель этой задачи.

Пусть — количество товара в тоннах, предназначенное к перевозке из склада в магазин. Набор чисел

составляет план перевозок. Так как в данном случае суммарные запасы равны суммарным потребностям: 50 + 100 = 30 + 40 + 80, то с каждого склада должен быть вывезен весь товар. Это приводит к уравнениям

Поскольку потребность каждого магазина также должна быть удовлетворена, то имеем еще три уравнения: Очевидно также, что

Суммарная стоимость всех перевозок задается линейной функцией

В итоге имеем каноническую задачу линейного программирования:

при условиях (7.5) — (7.7).

Данная задача приводится к стандартной форме следующим образом. Преобразуем систему (7.5), (7.6) методом Гаусса к виду с базисными неизвестными и свободными неизвестными В силу (7.7) справедливы неравенства

Заменив в (7.8) базисные неизвестные по формулам (7.9), приведем целевую функцию к виду Таким образом, получаехМ задачу линейного программирования в стандартной форме

при условиях (7.10), (7.11), эквивалентную задаче в канонической форме.

Возможно, вас также заинтересует эта ссылка:

Графический метод решения задачи линейного программирования

Рассматривается задача ЛП в стандартной форме при Допустимое множество (заданное неравенствами) — выпуклое множество на плоскости Целевая функция имеет вид

Прямые вида где — постоянная, называются линиями уровня. Все линии уровня параллельны друг другу

и перпендикулярны общему вектору нормали

Задача линейного программирования с двумя переменными допускает решение графическим методом, который состоит в следующем:

• 1) строится допустимое множество
• 2) если — пустое множество, то задача неразрешима, так как система ограничений противоречива;
• 3) если — непустое множество, то рассматриваются линии уровня При монотонном увеличении от прямые смещаются параллельно в направлении вектора

Если при таком перемещении линии уровня существует первая общая точка линии уровня и множества то — минимум на множестве Если — последняя точка пересечения

линии уровня и множества то в этой точке достигается максимум на множестве Если при неограниченном уменьшении

параметра прямая пересекает множество то

Если аналогичное свойство справедливо при неограниченном увеличении параметра то

Задачи линейного программирования общего вида допускают решение графическим методом, если их можно преобразовать к задаче с двумя независимыми переменными.

Возможно, вас также заинтересует эта ссылка:

Задача 3.

Найти минимальное и максимальное значения целевой функции при условиях:

На рис. 7.1 изображены допустимое множество линия уровня и вектор нормали Перемещая линию

уровня по направлению вектора находим сначала точку минимума целевой функции а затем точку максимума

2. Решить следующую задачу линейного программирования:

После исключения переменных получим задачу с двумя переменными:

Решая последнюю задачу графическим методом (рис. 7.2), находим ее оптимальное решение

Затем вычисляем значения переменных исходной задачи, соответствующие координатам точки

В результате получаем оптимальное решение исходной задачи:

Возможно, вас также заинтересует эта ссылка:

Симплексный метод решения задачи линейною программирования

Для решения задач линейного программирования симплексным методом следует выполнить ряд подготовительных операций.

• 1. Привести задачу к каноническому виду.
• 2. Преобразовать систему ограничений (уравнений) к специальному виду, в котором переменные разделены на базисные и свободные, а соответствующее базисное решение — неотрицательное (оно называется допустимым базисным решением или опорным решением).

Пример такой системы:

где — базисные переменные, — свободные переменные

3. Исключить из целевой функции базисные переменные с помощью (7.12) и записать ее в виде

Коэффициенты называются оценками соответствующих переменных

Из (7.12), (7.13) следует, что на допустимом базисном решении

целевая функция принимает значение

После выполнения подготовительного этапа заполняется начальная симплекс-таблица (табл. 7.12):

Здесь и ниже используются следующие сокращения:

• 1. — базисные неизвестные.
• 2. — свободные члены.

Таблица соответствует системе уравнений (7.12) с присоединенной целевой функцией (7.13). Последняя строка таблицы называется строкой оценок.

Пусть решается задача о нахождении минимума функции

Тогда цель дальнейших симплексных преобразований таблиц состоит в нахождении новых допустимых базисных решений, на которых значение целевой функции уменьшается (или не увеличивается). Алгоритм симплексных преобразований следующий.

1. Если в строке оценок среди чисел имеется хотя бы одна положительная (например, а в соответствующем столбце

(разрешающем столбце) хотя бы один положительный элемент, то решение может быть улучшено. Среди указанных положительных элементов столбца в качестве разрешающего элемента выбирается тот, которому отвечает минимальное отношение

Если имеется несколько элементов с подобным свойством, то в качестве разрешающего выбирается любой из них. В таблице таким элементом является Далее над таблицей проводятся элементарные преобразования: переменная становится базисной, a — свободной. На новом базисном решении значение целевой функции не увеличивается, и снова анализируется строка оценок.

2. Если в строке оценок нет положительных чисел, то оптимальное решение найдено.

3. Если в строке оценок есть положительное число, а в соответствующем ей столбце нет положительных элементов, то задача линейного программирования не имеет решения. В задаче о нахождении минимума функции это обозначается так:

4. Если в последней строке нет положительных оценок, но при этом имеются свободные переменные, равные нулю, то задача имеет, по крайней мере, одно альтернативное решение (чтобы его получить, следует сделать еще одно преобразование, выбрав разрешающий столбец с нулевой оценкой).

Как правило, множество оптимальных решений совпадает с выпуклой оболочкой всех альтернативных (базисных) решений. Исключением является случай, когда в процессе перебора альтернативных решений возникает нулевая оценка, такая, что в соответствующем столбце нет положительных чисел.

При решении задачи о поиске максимума функции алгоритм меняется только в том, что разрешающий столбец выбирается по отрицательной оценке в последней строке.

Задача 4.

Решить симплекс-методом задачу:

Переменные — базисные. Исключив их из целевой функции, получаем На исходном базисном решении значение целевой функции

Заполним начальную симплексную таблицу 7.13 и преобразуем ее.

Все оценки в последней строке неположительные, следовательно, получено оптимальное решение

Заметим, что значения базисных переменных и целевой функции получены из первого столбца симплекс-таблицы.

Задача 5.

Решить задачу линейного программирования:

Преобразуем целевую функцию: Система имеет исходное базисное решение со значением целевой функции Заполним симплексную таблицу (табл. 7.14) и преобразуем ее в соответствии с алгоритмом.

В последней строке есть положительная оценка но в соответствующем столбце нет ни одного положительного элемента, следовательно, задача не имеет решения:

Задача 6.

Решить задачу линейного программирования:

Исходное базисное решение Заполним начальную симплексную таблицу с учетом того, что и выполним последовательность преобразований таблиц в соответствии с алгоритмом симплекс-метода.

Анализ третьей и четвертой таблиц показывает, что минимальное значение целевой функции достигается на соответствующих этим таблицам базисных решениях: и Следовательно, общее оптимальное решение имеет вид:

для отыскания допустимого базисного решения.

Метод искусственных переменных

Для решения задачи линейного программирования симплексным методом необходимо, чтобы исходная система ограничений-уравнений имела вид, допускающий неотрицательное базисное решение. Вели это пребование не выполнено, то можно решить симплекс-методом вспомогательную задачу, что приведет систему ограничений к нужному виду. Алгоритм решения вспомогательной задачи следующий.

1. Исходная система ограничений- уравнений переписывается в виде

где все свободные члены

2. В каждое уравнение системы (7.14) вводятся искусственные переменные

Решение системы (7.15) а сама система имеет допустимое базисное решение

3. Рассматривается вспомогательная целевая функция

и симплексным методом решается задача линейного программирования

при ограничениях (7.15).

Если эта задача имеет решение, то возможны два случая.

1) Тогда исходная система (7.14) не имеет неотрицательных решений.

2) Система (7.14) имеет неотрицательное базисное решение. Если в последней симплекс-таблице вспомогательной задачи все искусственные переменные — свободные, то из этой таблицы несложно получить систему уравнений, эквивалентную (7.14) и преобразованную к виду, необходимому для решения исходной задачи линейного программирования.

Задача 7.

Преобразовать следующую систему уравнений к виду, допускающему неотрицательное базисное решение:

Введем искусственные переменные в двух последних уравнениях (в первом уравнении уже имеется базисная переменная

и рассмотрим вспомогательную целевую функцию Учитывая (7.16), получаем

Решим задачу при ограничениях (7.16). Решение дано в виде последовательности симплекс-таблиц (табл. 7.15).

Вспомогательная задача решена, искусственные переменные стали свободными переменными. Это означает, что система уравнений (7.15) преобразована к нужному виду

допускающему неотрицательное базисное решение

Взаимно двойственные задачи линейного программирования

Следующие задачи линейного программирования в стандартной форме, записанные в матричной форме, называются симметричной парой взаимно двойственных задач:

— матрица коэффициентов и транспонированная матрица; — столбцы неотрицательных иеизвестпых; — столбцы правых частей; — константа.

Решения задач I и II взаимосвязаны. Решив любую из них (исходную задачу), можно восстановить решение другой (двойственной задачи).

Первая теорема двойственности. Если исходная задача имеет оптимальное решение, то и двойственная ей также имеет оптимальное решение. При этом оптимальные значения целевых функций обеих задач равны:

Вторая теорема двойственности. Оптимальные решения

пары двойственных задач связаны между собой следующими соотношениями:

Замечание. Если исходная задача неразрешима из-за неограниченности целевой функции, то двойственная задача неразрешима из-за отсутствия допустимых решений (и наоборот).

Пусть теперь рассматривается общая задача линейного программирования. Приведем правила построения двойственной задачи. Матрицу коэффициентов при неизвестных дополним справа столбцом знаков неравенств и равенств для соответствующих ограничений, а также столбцом правых частей. Снизу матрицу дополним строкой ограничений для неизвестных: если при отсутствии ограничения на знак неизвестной; еще ниже добавим строку коэффициентов целевой функции. В результате получим следующую матрицу: Тогда аналогичная матрица двойственной задачи выглядит следующим образом: Из сравнения матриц (7.17) и (7.18) видно, что числовые части этих матриц получаются друг из друга транспонированием. Строка неравенств исходной задачи переходит без изменения в столбец неравенств двойственной задачи, причем символ переходит в знак Столбец неравенств исходной задачи переходит в строку ограничений на неизвестные, причем знаки неравенства меняются на противоположные, а знаки на знаки

При этом для пары двойственных задач с матрицами (7.17) и (7.18) остаются в силе формулировки первой и второй теорем двойственности.

Преобразуем пару двойственных задач в стандартной форме к канонической форме. При этом в задаче I появятся дополнительных неизвестных по числу основных ограничений, а в задаче дополнительных неизвестных Поэтому

число неизвестных в каждой задаче станет равным одному и тому же числу Можно установить взаимнооднозначное соответствие между этими неизвестными, а именно, основные неизвестные задачи I будут соответствовать дополнительным неизвестным задачи И, и дополнительные неизвестные задачи 1 — основным неизвестным задачи II.

Установленное соответствие позволяет находить решение двойственной задачи по заключительной симплекс-таблице основной задачи. А именно, выделим из последней симплекс-таблицы строку целевой функции. Если число, стоящее в ней, начиная со второго, взять с противоположным знаком, а затем воспользоваться соответствием между неизвестными обеих задач, то получим оптимальное решение двойственной задачи. Первое число в указанной строке дает искомый оптимум целевой функции.

Задача 8.

Сформулировать двойственную задачу линейного программирования для следующей задачи:

Составим расширенную матрицу данной задачи:

В соответствии с указанными правилами расширенная матрица двойственной задачи будет выглядеть следующим образом:

Поэтому развернутая запись двойственной задачи имеет вид:

Задача 9.

Найти решение следующей задачи линейного программирования, используя первую и вторую теоремы двойственности:

По общему правилу составим двойственную задачу:

Двойственная задача совпадает с задачей из § 7.2, которая была решена графическим методом, и ее оптимальное решение

Чтобы найти оптимальное решение исходной задачи, заметим, прежде всего, что выполняются строгие неравенства Этим переменным соответствуют первые два неравенства исходной задачи, которые по второй теореме двойственности обращаются в равенства:

Чтобы найти недостающее уравнение, подставим значения в неравенства двойственной задачи:

Поскольку третье неравенство строгое, то по второй теореме двойственности соответствующая этому неравенству переменная Таким образом, имеем систему уравнений:

откуда При этом достигается минимум функции что совпадает с ранее найденным значением

Задача 10.

Решить симплексным методом задачу ЛП. По заключительной таблице найти решение двойственной задачи.

Для решения задачи ЛП симплекс-методом введем дополнительные переменные и изменим знак целевой функции

Запишем исходную симилекс-таблицу для данной задачи и решим ее симплекс-методом (табл. 7.16):

Поскольку в строке коэффициентов целевой функции все коэффициенты неположительные, то решение исходной задачи таково: на базисном решении Поэтому исходная задача имеет решение

Двойственная задача к исходной выглядит следующим образом:

Установим соответствие между неизвестными исходной и двойственной задач, записанными в канонической форме:

поэтому из строки коэффициентов целевой функции последовательно находим:

Таким образом, решение двойственной задачи на базисном решении

Возможно, вас также заинтересует эта ссылка:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник