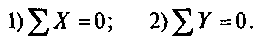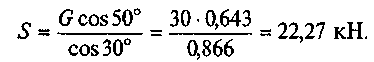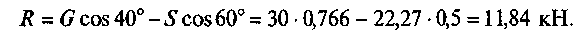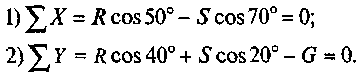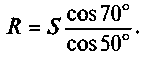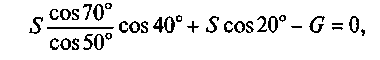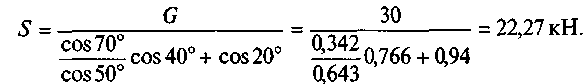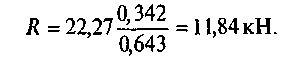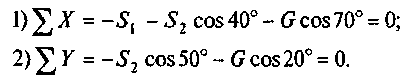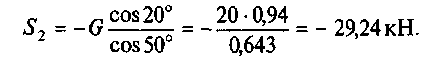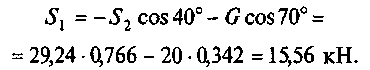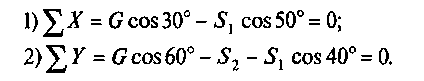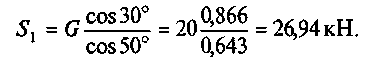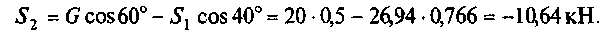Задачи определение реакции идеальных связей аналитическим способом

Решение задач на определение реакции связей

Два абсолютно жестких стержня АВ и АС соединены шарниром в точке А и прикреплены к полу шарнирами В и С, образуя с полом соответственно углы 45° и 60° (рис. 22 а). К валику шарнира А подвешен на нерастяжимой нити груз D, вес которого Р= 100 кг. Определить усилия, возникающие в стержне АВ и АС. Весом стержней и нити пренебречь.

Для определения усилий в стержнях АВ и АС следует рассмотреть равновесие шарнира А. Однако непосредственно приступить к исследованию равновесия узла А невозможно, так как он находится в равновесии под действием трех неизвестных сил: сил реакций стержней АВ и АС и реакции нити AD. Поэтому для определения силы реакции нити предварительно рассмотрим равновесие груза D. Груз D находится в равновесии под действием двух сил: веса Р и силы реакции нити Т. Эти силы направлены в противоположные стороны (рис. 22 б).

Учитывая условие равновесия груза, получим, что Т = Р = 100 Н.

Теперь, когда одна из трех сил, приложенных к шарниру А, известна, можно изучить равновесие шарнира А. К шарниру А приложена одна известная сила ­ реакция нити Т, направленная по вертикали вниз. Силы реакций N_АВ и N_АС стержней АВ и АС направлены вдоль стержней. На рис. 22 в эти три силы изображены приложенными в шарнире А (направлены ли силы N_АВ и N_АС вдоль стержней вверх или вниз уточнится в последующем решении задачи).

Графическое решение задачи.

При равновесии шарнира А равнодействующая всех трех сил должна быть равна нулю, следовательно, силы Т, N_АВ и N_АС образуют замкнутый силовой треугольник.

Построение силового треугольника (рис. 22 г) начинаем с силы Т, известной по величине и по направлению. Принимаем масштаб построения М = 2 Н / 1 мм Выбрав точку О, приложим к ней силу Т в выбранном масштабе построений. Длина отрезка графически представляющего вектор Т равняется 50 мм.

Затем, проведя через начало и конец силы Т прямые, соответственно параллельные стержням АС и АВ, получим в пересечении третью вершину Q силового треугольника OSQ. Изобразив на сторонах треугольника SQ и QO стрелки так, чтобы сумма трех сил Т, N_АВ и N_АС равнялась пулю (в каждой из вершин силового треугольника OSQ должен быть расположен конец только одной из трех сил), получим направления сил реакций N_АВ и N_АС и их величину в миллиметрах. Умножив длину в миллиметрах на масштаб получим:

Аналитическое решение задачи.

Принимаем направление оси y параллельно стержню АС, а направление оси x ей перпендикулярно, тогда угол между силой Т и осью y составит 30°, а угол между силой N_АВ и осью x составит 15° (рис. 22 в).

Составим уравнения равновесия:

из уравнения 1 N_АВ = T*sin30°/ cos15°= 100* sin30°/ cos15°=51,8 Н;

из уравнения 2 N_АС = T*cos 30°- N_АВ * sin 15° = 100* cos 30°-

Однородная балка, вес которой равен Р=100 Н, прикреплена к полу шарниром А и опирается другим концом в точке В на выступ вертикальной стены. Определить силы реакций выступа В и шарнира, если балка АВ разует угол 30° с горизонтом (см. рис. 23).

Вес балки Р= 100 Н, являющийся единственной задаваемой силой, приложен в середине балки в точке С и направлен по вертикали вниз. На балку наложены две связи: выступ В и шарнир А. Сила опорной реакции выступа В направлена пер­пендикулярно к балке. Направление силы реакции шарнира А заранее неизвестно. Однако в данной задаче можно воспользоваться теоремой о трех непараллельных силах и указать направление линии действия силы реакции шарнира А. Действительно, проведя линии действия сил Р и R_B (рис. 24 а), определим их точку пересечения О. Так как балка находится в равновесии под действием трех сил Р, R_B и R_A, то линии действия этих сил должны пересечься в одной точке, т. е. линия действия силы реакции шарнира R_A должна пройти через эту точку О. Поэтому проводим линию действия силы реакции шарнира R_А через ее точку приложения — шарнир А и точку О.

Дальнейшее решение задачи не представляет затруднений.

Графический способ решения задачи

Строим замкнутый силовой треугольник. Из точки D, взятой вне основного рисунка, проводим силу Р, приняв масштаб построения М =1 Н/1 мм. Через начало и конец силы Р ( отрезок DE = 100 мм) проводим прямые DN и ЕК, соответственно параллельные линиям действия сил R_А и R_В (рис.24 б). В точке пересечения прямых DN и ЕК находим третью вершину М силового треугольника DEM. Направляем векторы сил так, чтобы в каждой из вершин силового треугольника был расположен конец одной из сил. Определяем длину отрезков EM и MD, с учетом выбранного масштаба:

Аналитический способ решения задачи

Принимаем направление оси y параллельно реакции R_B, а направление оси x ей перпендикулярно, тогда угол между силой P и осью y составит 30°, а угол между силой R_А и осью x нам неизвестен — обозначим его α (рис. 25 а).

Определим угол α.

Из прямоугольного треугольника ОВС: ОВ = ВС/tg30° = a/0.577

Из прямоугольного треугольника ОВА: tg α = ОВ/АВ = a/(0.577*2a) = 0.866

Отсюда α = 40°54’38»

Составим уравнения равновесия:

из уравнения 1 R_А = P*sin30°/ cos40°54’38»= 100* sin30°/cos40°54’38»= 66,14 Н;

из уравнения 2 R_B = P*cos 30°- R_А * sin 40°54’38» = 100* cos 30°-

Источник

Раздел I самостоятельные и контрольные работы

Глава 1 теоретическая механика. Статика

1.1. Определение реакций идеальных связей аналитическим способом

1. Указывают точку, равновесие которой рассматривается. В задачах для самостоятельной работы такой точкой является центр тяжести тела или точка пересечения всех стержней и ни­тей.

2. Прикладывают к рассматриваемой точке активные силы. В задачах для самостоятельной работы активными силами явля­ются собственный вес тела или вес груза, которые направлены вниз (правильнее — к центру тяжести земли). При наличии бло­ка вес груза действует на рассматриваемую точку вдоль нити. Направление действия этой силы устанавливается из чертежа. Вес тела принято обозначать буквой G.

3. Мысленно отбрасывают связи, заменяя их действие реакция­ми связей. В предлагаемых задачах используются три вида свя­зей — идеально гладкая плоскость, идеально жесткие прямоли­нейные стержни и идеально гибкие нити, — в дальнейшем име­нуемые соответственно плоскостью, стержнем и нитью.

При замене связей их реакциями следует помнить, что реак­ция плоскости направлена по нормали (перпендикуляру) к ней в точке контакта (соприкосновения), а реакции стержня и нити — по их осям. При этом реакция плоскости направлена от нее и проходит через центр тяжести тела, а реакция нити — от рас­сматриваемой точки или тела (нить всегда испытывает растяже­ние). Направление реакции стержня заранее неизвестно, поэто­му оно может быть принято произвольно. Если направление ре­акции стержня трудно определить из схемы, то его принимают растянутым, и реакцию направляют от рассматриваемой точки. Истинное направление будет установлено после решения урав­нений.

Реакции нити и стержня принято называть усилиями. Реак­цию плоскости обозначают буквой R, а усилие в нити и стерж­не — S или N. В дальнейшем, если не указывается вид связи или говорится о разных связях, то будет применяться термин «реак­ция».

К рассматриваемой точке прикладывают реакции связей. Луч­ше сделать это на отдельном чертеже, выполненном схематиче­ски, придерживаясь масштаба при изображении углов. В резуль­тате получают систему трех сходящихся сил. Активная сила (груз или собственный вес тела) известна, а реакции связей (их две) не­известны.

4. Выбирают положение прямоугольной системы координат, Начало координат совмещают с точкой, равновесие которой рас­сматривается. Положение осей может быть выбрано произволь­но и на конечном результате при правильном решении это не отражается. Обычно используют один из двух приемов для выбо­ра направления осей координат. Первый: одну из осей (любую) направляют так, чтобы она совпала с направлением одной из не­известных реакций, а другая при этом составляла бы с первой угол 90°. Второй: ось у направляют вертикально, а ось х — гори­зонтально. В частном случае возможен еще один прием для рас­положения осей: если система сил имеет ось симметрии, то одну из координатных осей совмещают с ней.

Во всех случаях следует определить углы между реакциями и координатными осями и указать их на чертеже.

5. Составляют уравнения равновесия вида:

Напомним, что проекцией силы на ось является произведение модуля (величины) этой силы на косинус угла между направления­ми действия силы и оси. Если угол между направлениями силы и оси острый, то перед величиной проекции ставится знак «плюс», т. е. сила и ось направлены в одну сторону, если они направлены в противоположные стороны, то ставиться знак «минус».

Решают систему двух уравнений с двумя неизвестными. При этом если одна из осей совпадает с неизвестной реакцией, то одно из двух уравнений содержит только одно неизвестное, что упрощает решение системы.

Если ответ получится со знаком «минус», то это означает, что направление реакции на чертеже было выбрано неверно, т.е. если до составления уравнений равновесия стержень предпола­гался растянутым, то в действительности он будет сжатым, и на­оборот. Такой ответ не является ошибкой решения (если оно выполнено верно), так как чертеж и ответ вместе дают возмож­ность указать истинное направление реакции.

6. Выполняют проверку решения. Обычно она делается графи­ческим или другими способами, но может быть выполнена и аналитически. Для этого следует изменить положение осей ко­ординат и решить задачу в новой системе. Ответы должны быть одинаковыми.

Пример 1. Определить величину и направление реакций свя­зей для схемы, приведенной на рис. 1, а под действием груза С = 30 кН. Проверить правильность определения реакций.

Решение. 1. В задаче рассматривается равновесие тела, опи­рающегося на плоскость и подвешенного на нити. Заменим тело точкой 0, совпадающей с центром тяжести.

2. Приложим к точке О активную силу, которой является соб­ственный вес тела G. Направим ее вниз (рис. 1, б).

3. Мысленно отбросим связи — плоскость и нить. Заменим их действие на точку 0 реакциями связей. Реакция плоскости (обо­значим ее R) проходит по нормали к плоскости в точке А, а ре­акция или усилие в нити (обозначим ее 5) — по нити от точки. Обе реакции и вес тела или линии их действия должны пересе­каться в точке 0.

Изобразим действующие силы в виде системы трех сходя­щихся сил на отдельном чертеже (рис. 1, в).

4. Выберем положение системы координат. Начало координат совмещаем с точкой 0. Ось х совмещаем с направлением линии действия реакции R, а ось у направим перпендикулярно оси х (рис. 1, г). Определим утлы между осями координат и реакциями R и S. Обычно рис. 1, б и 1, в не выполняют отдельно, а сразу от рис. 1, а переходят к рис. 1, г. Можно было ось у совместить с усилием S, и ось х направить по углом 90°, тогда решение было бы другим.

5. Составим сумму проекций всех сил на оси координат:

1) £ X = R + S cos 60° — G cos 40° — 0;

2)]Ty = Scos30 0 -Gcos50 0 = 0.

Решим систему уравнений. Из второго уравнения находим

Из первого уравнения находим

6. Проверим решение, для чего расположим оси координат, как показано на рис. 1, д. Составим уравнения равновесия для вновь принятых осей:

Решим систему уравнений способом подстановки. Из первого уравнения найдем R:

Подставим это выражение во второе уравнение:

Теперь найдем R:

Очевидно, что при расположении осей, как показано на рис. 1, д, вычисления оказались более сложными.

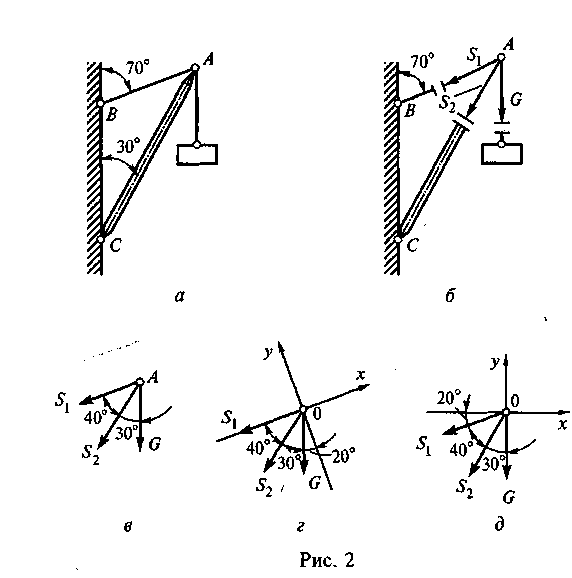
Пример 2. Определить усилия в нити и стержне кронштейна, показанного на рис. 2, а, если G= 20 кН.

Решение. 1. Рассмотрим равновесие точки А (или узла А), в которой сходятся все стержни и нити.

2. Активной силой является вес груза G, направленный вниз (рис. 2, б).

3. Отбросим связи: стержень и нить. Усилие в нити обозна­чим S\ и направим от точки А, так как нить может испытывать только растяжение. Усилие в стержне обозначим S₂ и тоже на­правим от точки А, предполагая что стержень АС растянут (рис. 2, б).

Выполним на отдельном чертеже схему действия сил в точке А (рис. 2, в).

4. Выберем положение системы координат. Начало коорди­нат совмещаем с точкой А (рис. 2, г). Ось х совмещаем с лини­ей действия усилия S₁ , а ось у располагаем перпендикулярно оси х. Укажем углы между осями координат и усилиями Si и S₂.

5. Составим уравнения равновесия:

Из второго уравнения находим

Из первого уравнения находим

Знак «минус» перед S₂ свидетельствует о том, что стержень АС не растянут, как предполагалось, а сжат.

6. Проверку решения предлагаем выполнить самостоятельно, расположив оси координат так, как показано на рис. 2, д.

Величина усилий зависит от углов наклона стержня и нити. Например, если на рис. 2, а угол 70° заменить на 60°, сохранив угол 30 Р , то усилия будут равны: Si = 20 кН, S₂ = -34,64 кН. А при угле 50° S_< = 29,26 кН, S₂ = -44,8 кН. Оба усилия растут и становятся больше веса груза.

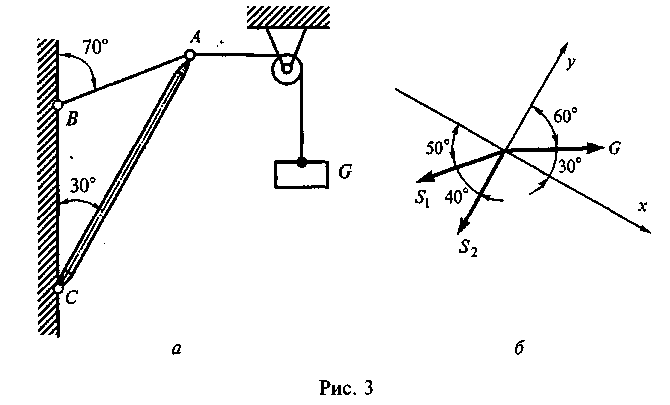
Пример 3. Как изменятся усилия в стержне и нити, если груз будет перекинут через блок, как показано на рис. 3, а>.

Остальные данные — в примере 2.

Решение. 1. Рассматриваемой точкой остается точка А. 1. Активная сила (вес груза G) действует на точку горизон­тально слева направо, так как груз перекинут через блок.

3. Усилия Si и S₂ прикладываем к точке А, как в примере 2.

4. Выбираем систему координат, как показано на рис. 3, б.

5. Составляем и решаем уравнения равновесия:

Из первого уравнения находим

Из второго уравнения находим

Ответ: Si = 26,94 кН; S₂ = -10,64 кН при принятом направле­нии усилий на чертеже. Усилие Si увеличилось, S₂ — уменьши­лось, а знаки не изменились.

Задание для самостоятельной работы 1. Определить величину и на­правление реакций связей по данным одного из вариантов, показан­ных на рис. 4.

Источник