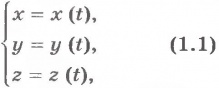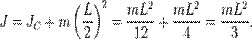Задачи механики способы описания движения материальной точки

Три способа описания движения материальной точки. Векторный способ. Определение скорости и ускорения

Теоретическая механика как наука. Три основных раздела ТМ. Кинематика. Основные задачи кинематики.

Теоретическая механика – наука об общих законах механических взаимодействий между материальными телами, а также об общих законах движения тел по отношению друг к другу.

Теоретическая механика, преподаваемая в техническом вузе, содержит три раздела: кинематику, статику и динамику:

Кинематика – часть механики, в которой изучаются зависимости между величинами, характеризующими состояние движения систем, но не рассматриваются причины, вызывающие изменение состояния движения.

Статика – это учение о равновесии совокупности тел некоторой системы отсчета.

Динамика – часть механики, в которой рассматривается влияние сил на состояние движения систем материальных объектов.

Основная задача кинематики заключается в установлении (при помощи тех или иных математических методов) способов задания движения точек или тел и в определении по уравнениям их движений соответствующих кинематических характеристик движения, таких, как траектории, скорости и ускорения движущихся точек, угловые скорости и угловые ускорения вращающихся тел и др.

Три способа описания движения материальной точки. Векторный способ. Определение скорости и ускорения.

Естественный способ. Этим способом пользуются, если из­вестна траектория движения точки. Траекторией называется совокупность точек пространства, через которые проходит движущаяся материальная частица. Это линия, которую она вычерчивает в пространстве.

Координатный способ. Будем задавать положение точки с помощью координат. Если точка движется, то ее координаты изменяются с течением времени. Так как координаты точки зависят от времени, то можно сказать, что они являются функциями времени. В зависимости от формы траектории все движения точки делятся на прямолинейные и криволинейные. Если траекторией является прямая линия, движение точки называется прямолинейным, а если кривая — криволинейным.

Математически это принято записывать в виде:

Векторный способ. Положение точки можно задать, как известно, и с помощью радиус-вектора. При движении материальной точки радиус-вектор, определяющий ее положение, с течением времени изменяется, т. е. является функцией времени: r=r(t) (стрелочки над ними нужны). Одна такая функция равняется трем функциям (1.1). Если ввести единичные векторы i, j, k ( i = j = k = 1), направленные соответственно вдоль осей x, y и z то, очевидно, закон движения может быть представлен в виде:

r(t) = x(t)i + y(t)j + z(t)k.

Преимущество векторной формы записи перед координатной в компактности (вместо трех величин оперируют с одной) и часто в большей наглядности.

Источник

Задачи механики способы описания движения материальной точки

Движение. Виды движений. Описание движения. Система отсчета.

Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.

А) Равномерное прямолинейное движение материальной точки.

Б) Равноускоренное прямолинейное движение материальной точки.

В) Движение тела по дуге окружности с постоянной по модулю скоростью.

Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.

1. Векторный способ описания движения

ОПРЕДЕЛЕНИЕ: Векторный способ описания движения – это описание изменения радиус-вектора материальной точки в пространстве с течением времени.

Рассмотрим движение точки М в некоторой системе отсчета Oxyz (рис.1). Зададим радиус-вектор точки r — вектор, соединяющий начало координат с этой точкой.

При движении точки M вектор r будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость r = r ( t ) представляет собой закон движения в векторном виде.

В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение s точки.

2. Координатный способ описания движения

ОПРЕДЕЛЕНИЕ: Координатный способ описания движения – описание изменения во времени координат точки в выбранной системе отсчета.

В декартовой системе координат положение точки определяется тройкой чисел ( x , y , z ) — ее декартовыми координатами.

Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений: x = x ( t ), y = y ( t ), z = z ( t )

Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки: r_x = x , r_y = y , r_z = z .

3. Естественный способ описания движения

ОПРЕДЕЛЕНИЕ: Естественный способ описания движения – описание движения вдоль траектории. Этим способом пользуются, когда траектория точки заранее известна.

Пусть точка М движется вдоль траектории АВ в системе отсчета Oxyz (рис.3). Выберем на траектории какую-нибудь неподвижную точку О 1 , которую будем считать началом отсчета, и определим положительное и отрицательное направления. Тогда положение точки M будет определяться расстоянием S от точки О 1 . При движении точка М переместится в точку М 1 , соответственно изменится ее расстояние от точки О 1 . Таким образом, расстояние S зависит от времени, а характер этой зависимости позволит определить положение точки М на траектории в любой момент времени. Закон движения в этом случае имеет вид: s = s ( t ) .

Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.

Источник

Задачи механики. Естественный и векторный способы описания движения материальной точки (МТ)

Задачи механики. Естественный и векторный способы описания движения материальной точки (МТ)

Меха́ника— область физики, изучающая движение материальных тел и взаимодействие между ними. Основная задача механики – определить положение тела в любой момент времени. Механика где? Кинематика

почему? Динамика

Материа́льная то́чка (частица) — простейшая физическая модель в механике — идеальное тело, размеры которого равны нулю, можно также считать размеры тела бесконечно малыми по сравнению с другими размерами или расстояниями в пределах допущений исследуемой задачи. Положение точки относительно тела отсчета можно задавать естественным и векторным способами. Естественный способ описания движения МТ основывается на том что нам известна траектория движения. 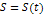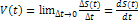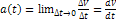Зная её мы легко можем найти путь( ), перемеще- ние, скорость( , ускорение . Недостатки: необход начальные сведения о траектории, проблема двух тел. При векторномспособе положение частицы по отношению к системе отсчета определяется с помощью радиус-вектора r. Траектория точки годограф вектора r, -геометрическое место концов радиус-вектора. В большинстве случаев траектория невидима и допускает лишь математическое описание. Модуль радиус-вектора равен расстоянию от траектории до начала координат.

Основные понятия кинематики. Векторный и координатный способы описания движения материальной точки.

Кинематика -рассматривает движение тел без выяснения причин этого движения. Кинематика-раздел мех., в котором изучается мех движ тел независимо от причин, вызывающих и изменяющих это движ. Тело отсчёта — тело, условно принимаемое за неподвижное, относительно которого рассматривается движение др тел. Мех движение-изменение положения тел относительно др тел в пространстве с течением времени. Сист отсчёта состоит из тела отсчёта, сист координат и прибора для измерения времени. МТ- тело, размерами которого можно пренебречь в данных усл. Траектория- воображаемая линия, которую опис движущаяся МТ.1Координатный способ. Это наиболее универсальный и ис­черпывающий способ описания движения. Он предполагает задание: а) системы координат (не обязательно декартовой) q1, q2, q3; б) начало отсчета времени t; в) закона движения точки, т.е. функций q1(t), q2(t), q3(t). Говоря о координатах точки, мы всегда будем иметь в виду ее декартовы координаты. 2. Векторный способ. Положение точки в пространстве может быть определено также и радиус-вектором, проведенным из некоторо­го начала в данную точку (рис. 2). В этом случае для описания дви­жения необходимо задать: а) начало отсчета радиус-вектора r; б) начало отсчета времени t; в) закон движения точки r(t)

. 3.Классификация механических движений материальной точки. Основные соотношения кинематики прямолинейного движения.

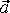
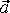
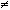
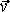
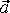
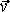
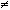
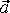
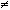
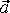
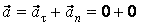
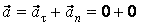
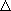
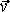
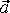
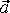
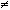
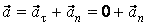
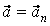
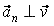
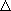
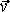
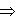
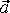
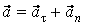
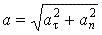
Классификацию видов движения материальной точки подразделяются на два вида: прямолинейное ( _n = 0) и криволинейное ( _n 0). В зависимости от характера изменения скорости механические движения подразделяются также на два вида: равномерное (| | = const, _t = 0) и неравномерное (| | const и | | const). 1. Прямолинейное движение ( _n = 0) а) Равномерное прямолинейное движение (модуль скорости и направление скорости не изменяются . ; = const. б) Равномерное прямолинейное движение (модуль скорости изменяется на равную величину за любые равные интервалы времени: | | = const, направление скорости не изменяется. 2. Криволинейное движение(движение материальной точки по окружности – простейшее криволинейное движение)а) Равномерное движение материальной точки по окружности (модуль скорости _t не изменяется, но направление скорости изменяется _t 0 изменяется. ; ,т.е. . б) Равнопеременное движение материальной точки по окружности (модуль скорости изменяется, но | | = const _t 0 и направление скорости изменяется

; . Если направления векторов тангенциального ускорения и скорости совпадают– это равноускоренное движение материальной точки по окружности. Если направления векторов тангенциального ускорения и скорости противоположны – это равнозамедленное движение материальной точки по окружности.

Момент инерции. Примеры вычисления моментов инерции твердых тел.

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Измеряется: кг·м².Обозначается: I или J.Примеры:

тело	Момент инерции
Полый цилиндр радиуса R	mR 2
Сплошной диск	½ mR 2
Шар	2/5 mR 2

Теорема Штейнера. Примеры ее применения.

Если известен момент инерции тела относительно оси проходящей ч/з его центр масс то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции J_c относительно параллельной оси проходящей ч/з центр масс С тела, сложенной с произведением массы m тела на квадрат расстояния а между осями: J= J_c + ma 2 . 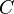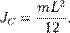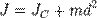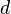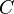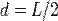Пример:Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью ) равен Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен где — расстояние между искомой осью и осью . В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти положив в последней формуле :

Уравнение плоской волны.

Плоская волна — волна, у которой направление распространения одинаково во всех точках пространства. ; .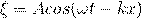

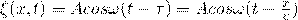
Волновое уравнение.

Волновое уравнение в математике — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно линейная: звук в газах, жидкостях и твёрдых телах) и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн. 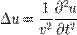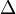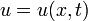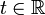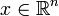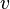В общем случае волновое уравнение записывается в виде , где — оператор Лапласа, — неизвестная функция, — время, — пространственная переменная, — фазовая скорость.

Основные понятия гидродинамики. Теорема неразрывности и ее следствия.

Задачи механики. Естественный и векторный способы описания движения материальной точки (МТ)

Меха́ника— область физики, изучающая движение материальных тел и взаимодействие между ними. Основная задача механики – определить положение тела в любой момент времени. Механика где? Кинематика

почему? Динамика

Материа́льная то́чка (частица) — простейшая физическая модель в механике — идеальное тело, размеры которого равны нулю, можно также считать размеры тела бесконечно малыми по сравнению с другими размерами или расстояниями в пределах допущений исследуемой задачи. Положение точки относительно тела отсчета можно задавать естественным и векторным способами. Естественный способ описания движения МТ основывается на том что нам известна траектория движения. 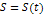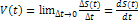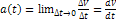Зная её мы легко можем найти путь( ), перемеще- ние, скорость( , ускорение . Недостатки: необход начальные сведения о траектории, проблема двух тел. При векторномспособе положение частицы по отношению к системе отсчета определяется с помощью радиус-вектора r. Траектория точки годограф вектора r, -геометрическое место концов радиус-вектора. В большинстве случаев траектория невидима и допускает лишь математическое описание. Модуль радиус-вектора равен расстоянию от траектории до начала координат.

Основные понятия кинематики. Векторный и координатный способы описания движения материальной точки.

Кинематика -рассматривает движение тел без выяснения причин этого движения. Кинематика-раздел мех., в котором изучается мех движ тел независимо от причин, вызывающих и изменяющих это движ. Тело отсчёта — тело, условно принимаемое за неподвижное, относительно которого рассматривается движение др тел. Мех движение-изменение положения тел относительно др тел в пространстве с течением времени. Сист отсчёта состоит из тела отсчёта, сист координат и прибора для измерения времени. МТ- тело, размерами которого можно пренебречь в данных усл. Траектория- воображаемая линия, которую опис движущаяся МТ.1Координатный способ. Это наиболее универсальный и ис­черпывающий способ описания движения. Он предполагает задание: а) системы координат (не обязательно декартовой) q1, q2, q3; б) начало отсчета времени t; в) закона движения точки, т.е. функций q1(t), q2(t), q3(t). Говоря о координатах точки, мы всегда будем иметь в виду ее декартовы координаты. 2. Векторный способ. Положение точки в пространстве может быть определено также и радиус-вектором, проведенным из некоторо­го начала в данную точку (рис. 2). В этом случае для описания дви­жения необходимо задать: а) начало отсчета радиус-вектора r; б) начало отсчета времени t; в) закон движения точки r(t)

. 3.Классификация механических движений материальной точки. Основные соотношения кинематики прямолинейного движения.

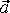
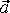
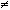
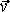
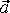
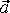
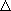
Классификацию видов движения материальной точки подразделяются на два вида: прямолинейное ( _n = 0) и криволинейное ( _n 0). В зависимости от характера изменения скорости механические движения подразделяются также на два вида: равномерное (| | = const, _t = 0) и неравномерное (| | const и | | const). 1. Прямолинейное движение ( _n = 0) а) Равномерное прямолинейное движение (модуль скорости и направление скорости не изменяются . ; = const. б) Равномерное прямолинейное движение (модуль скорости изменяется на равную величину за любые равные интервалы времени: | | = const, направление скорости не изменяется. 2. Криволинейное движение(движение материальной точки по окружности – простейшее криволинейное движение)а) Равномерное движение материальной точки по окружности (модуль скорости _t не изменяется, но направление скорости изменяется _t 0 изменяется. ; ,т.е. . б) Равнопеременное движение материальной точки по окружности (модуль скорости изменяется, но | | = const _t 0 и направление скорости изменяется

; . Если направления векторов тангенциального ускорения и скорости совпадают– это равноускоренное движение материальной точки по окружности. Если направления векторов тангенциального ускорения и скорости противоположны – это равнозамедленное движение материальной точки по окружности.

Источник