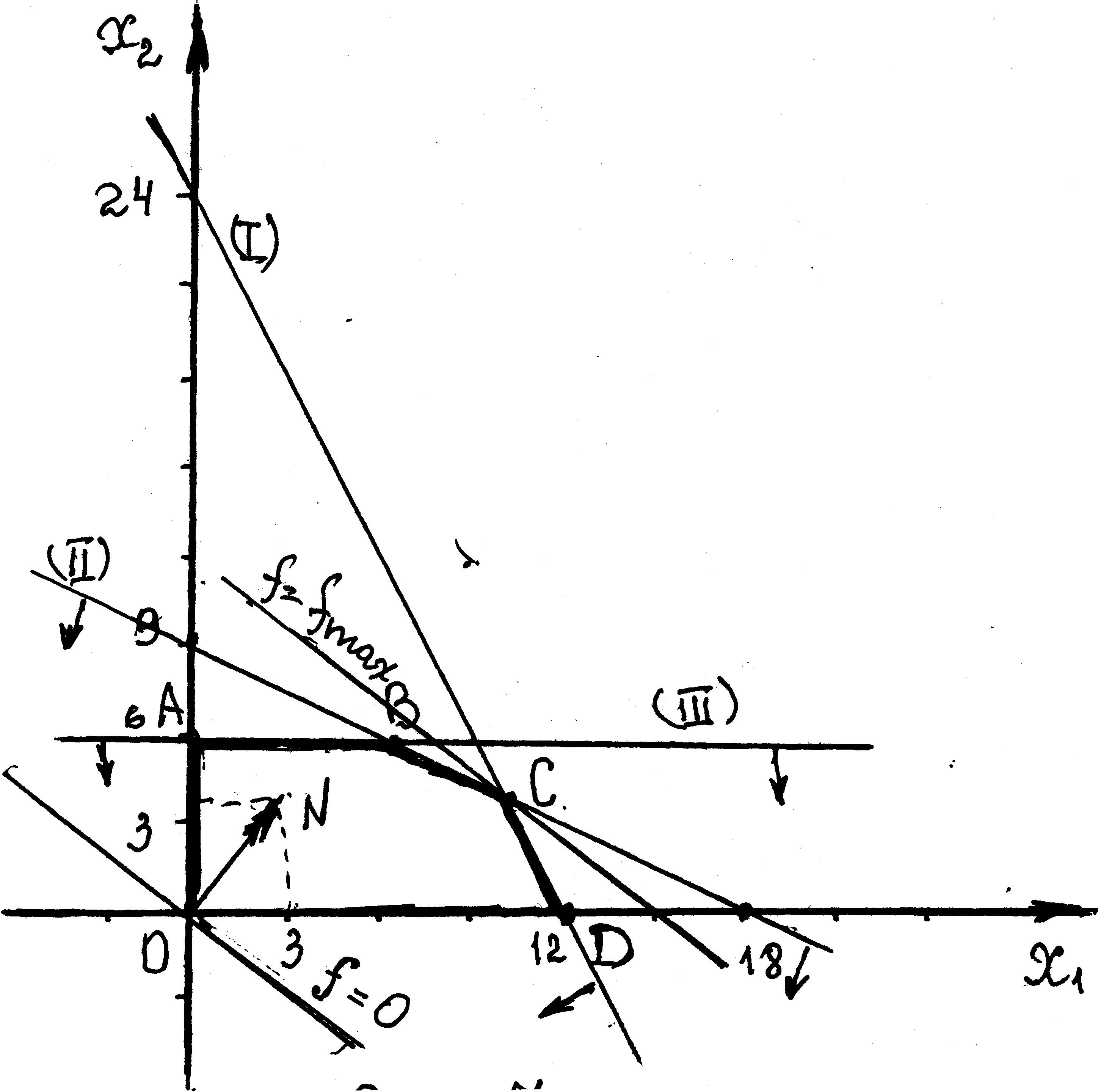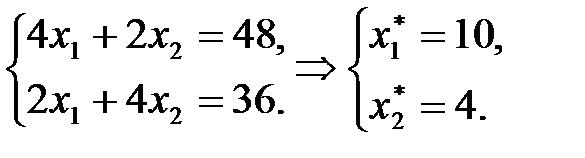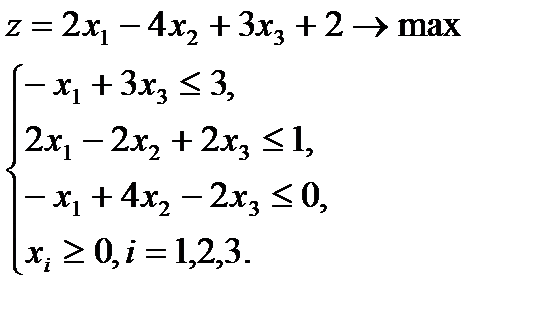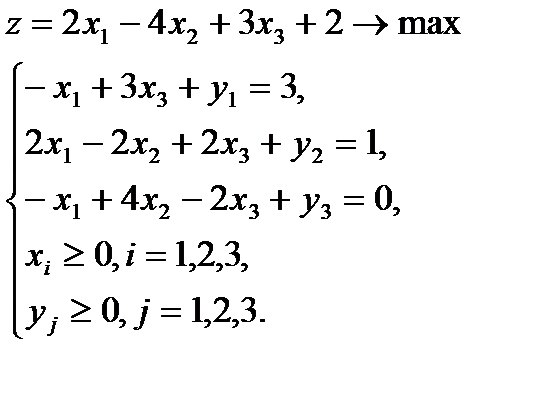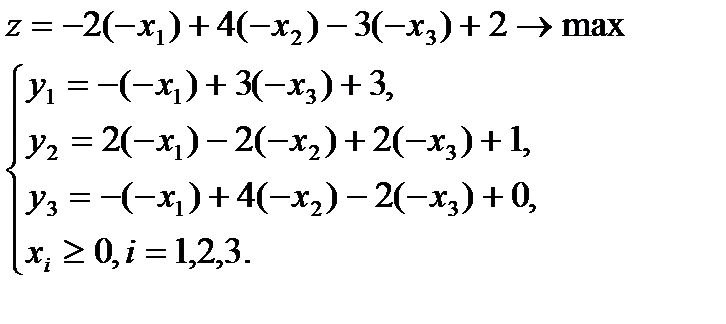Тема 5. Линейные задачи оптимизации
Рассмотрим ряд конкретных прикладных задач, в которых надо найти экстремум (максимум или минимум) линейной функции многих переменных при наличии линейных ограничений, т.е. равенств или неравенств, связывающих эти переменные.
Область математики, разрабатывающая теорию и численные методы решения таких задач – линейное программирование. Общие методы решения таких задач мы рассмотрим позже.
Задачи будем решать графическим способом. Его целесообразно использовать для решения задач с двумя переменными, ограничения которых заданы в виде неравенств и равенств, или для задач со многими переменными, ограничения которых заданы равенствами, при условии, что в этой системе не более двух свободных переменных. Ограничимся первыми.
Для практического решения экономических задач математическими методами надо составить математическую модель задачи, т.е. записать ее с помощью математических выражений.
Задача 10. Предприятие для производства двух видов продукции может использовать 48 станков типа А, 36 станков типа В и 12 станков типа С. По техническим условиям на производство единицы продукции первого вида требуется занять 4 станка А и 2 станка В, для производства единицы продукции второго вида требуется 2 станка А, 4 станка В и 2 станка С.
Прибыль от реализации одной единицы продукции первого вида – 3 тысячи рублей, второго вида – 4 тысячи рублей. Составить план выпуска продукции, обеспечивающий максимальную прибыль.
Решение. Составим математическую модель задачи. Обозначим через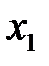 
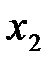
и 
соответственно количество единиц продукции первого и второго видов.
Перейдем к анализу технических условий производства. Для производства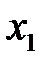 
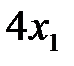
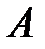
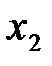
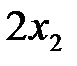
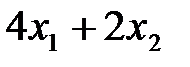
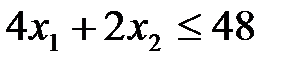
изделий первого вида требуется 
станков 
, а для 
второго вида – 
станков А, а для производства всей продукции 
, но их можно использовать не более чем имеется в наличии, следовательно,
. (1)
Точно так же получим ограничения по станкам соответственно типов В и С:
, (2)
. (3)
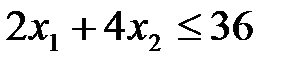
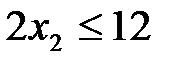
По смыслу задачи: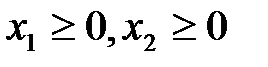 
. (4)
Любой план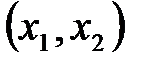 
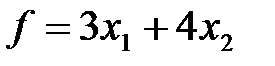
, удовлетворяющий ограничениям (1)-(4), будет допустимым и даст предприятию прибыль (в тыс. руб.)
. (5)
Итак, математически задача отыскания оптимального плана производства изделий сводится к определению таких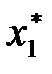 
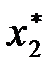
и 
, удовлетворяющих линейным ограничениям (1)-(4), которые доставляют максимум линейной функции (5).
Соотношения (1)-(5) образуют математическую модель задачи:
. (6)
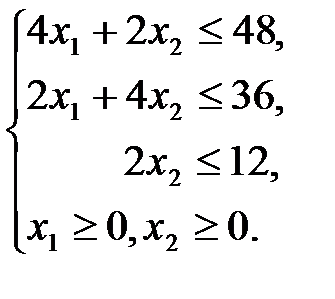
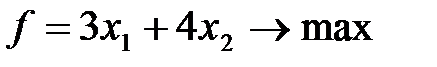
Решим задачу (6) графическим методом. Для построения области допустимых значений строим соответствующие данным неравенствам граничные прямые: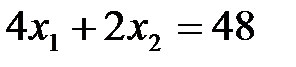 
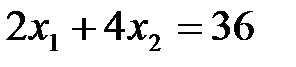
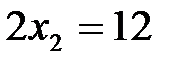
– (I),
– (II),
– (III)
по точкам пересечения с осями координат. Для прямой (I) это точки: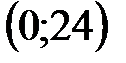 
, 
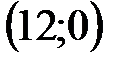
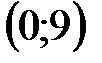
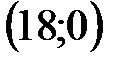
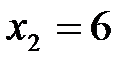
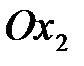
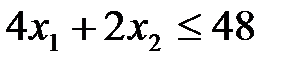
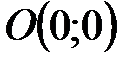
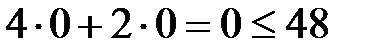
; для (II): 
, 
; прямая (III) 
параллельна оси 
. Выберем масштаб 1 : 3 (рис. 1). Далее находим полуплоскости, в которых выполняются данные неравенства. Так неравенство определяет полуплоскость с граничной прямой (I), в которой расположена точка 
( 
, т.е. это неравенство удовлетворяется координатами точки 
).
Область допустимых решений определяется как общая часть пяти полуплоскостей, соответствующим трем данным неравенствам, и неравенствами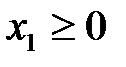 
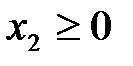
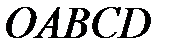
(правая координатная полуплоскость) и 
(верхняя координатная полуплоскость). Это многоугольник 
.
Теперь обратимся к функции (5), которая носит название целевой. Линии уровня функции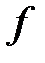 
: 
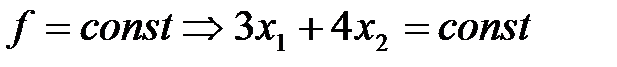
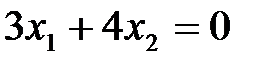
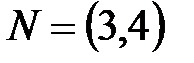
– это семейство паралельных прямых. Построим одну из них, например, 
, ее вектор нормали 
и она проходит через начало координат.
Можно доказать, что при перемещении линии уровня линейного функционала параллельно себе в направлении вектора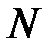 
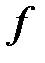
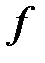
значение функции 
возрастает. Следовательно, наибольшее значение функции 
в области допустимых решений принимает в точке 
.
Найдем координаты этой точки, решив систему уравнений:
Подставим найденные значения в (5):
.
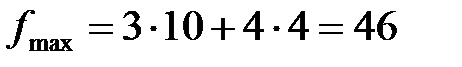
Ответ. Максимальное значение прибыли 46 тыс. рублей обеспечивает план выпуска продукции: 10 ед. продукции первого вида и 4 ед. продукции второго вида.
Пример 2. Животное должно получать ежедневно не менее 18 единиц вещества А и не менее 20 единиц вещества В. Один килограмм I вида корма содержит 6 ед. вещества А и 5 ед. вещества В. Один килограмм II вида корма содержит 3 ед. вещества А и 4 ед. вещества В. Цена корма I вида 10 руб., II вида – 8 руб. за кг.
Установить рацион кормления животных с учетом биологических требований, дающий минимальные затраты.
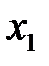
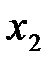
Решение. Обозначим через и кг соответственно количество кормов I и II видов, которые предполагается включить в рацион.
Количество единиц вещества А, содержащееся в рационе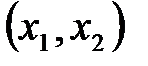 
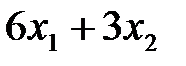
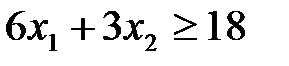
, можно выразить суммой 
. По условию эта величина не может быть меньше 18 единиц, т.е.
. (7)
Ограничение по содержанию вещества B в рационе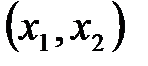 
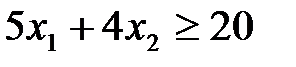
имеет вид:
. (8)
Естественно также, что
. (9)
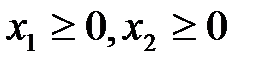
В принятых обозначениях стоимость рациона выражается в виде функции:
. (10)
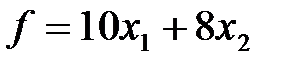
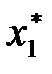
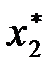
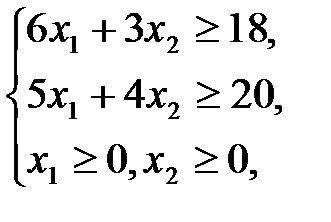
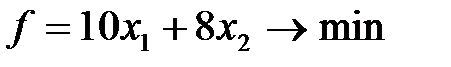
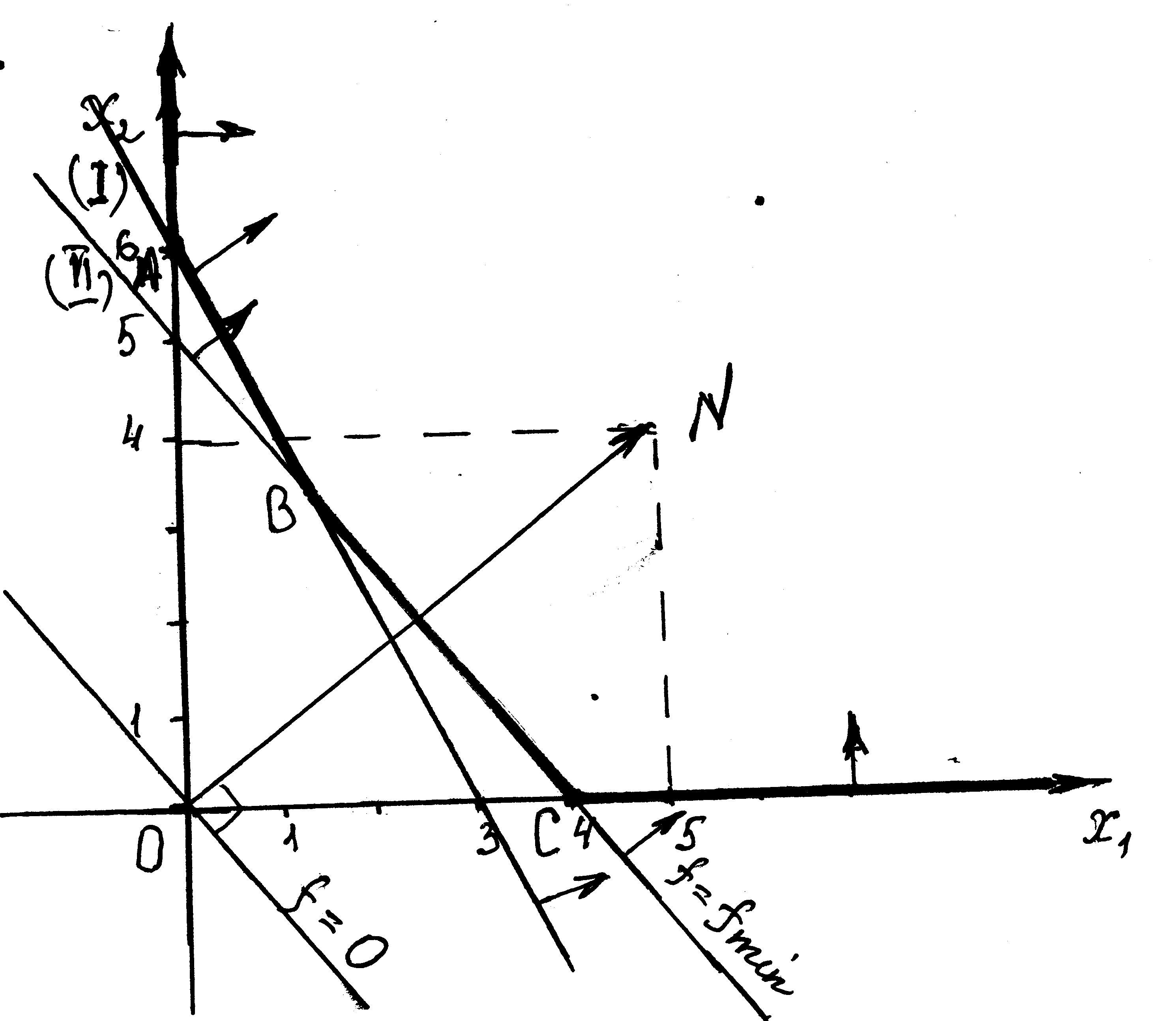
Итак, задача сводится к определению , , удовлетворяющих линейным ограничениям (7)-(9), при которых линейная функция (10) достигает наименьшего значения. Математическая модель задачи:
. (11)
Решим ее графическим методом. Проведем построение аналогично примеру 1.
Областью допустимых решений задачи является выпуклая многогранная неограниченная область х2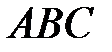 
х1 (рис.2).
Построим нулевую линию уровня
, тогда 
.
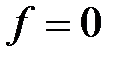
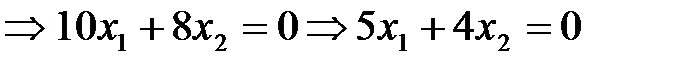
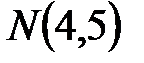
Перемещаем прямую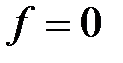 
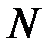
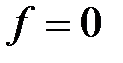
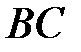
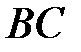
параллельно самой себе в направлении вектора 
, тогда точка ее входа в область допустимых решений даст нам решение задачи. Но прямая параллельна прямой линии (II), т.е. минимальное значение достигается во всех точках отрезка 
. Задача имеет неединственное решение. Найдем уравнение отрезка .
Так как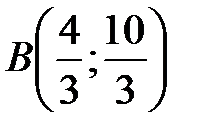 
, 
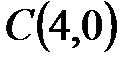
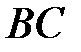
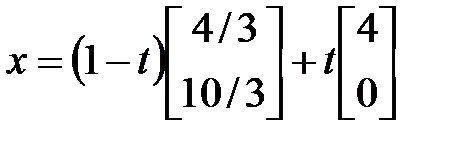
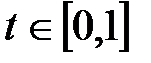
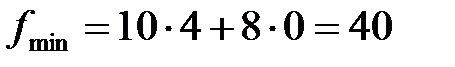
, то уравнение отрезка : 
, 
. Тогда 
(руб.)
Ответ: задача имеет неединственное решение. Минимальная стоимость рациона кормления – 40 рублей, оптимальный рацион можно рассчитать по формулам: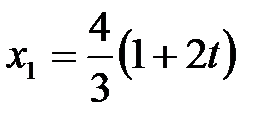 
, 
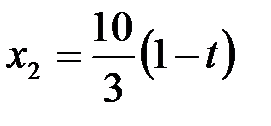
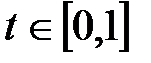
, где .
Из решений задач линейного программирования графическим методом мы можем сделать следующие основные выводы:
1. Если область допустимых решений задачи является выпуклым многогранником, то оптимальное решение задачи всегда существует и совпадает, по крайней мере, с одной из угловых точек этого многогранника.
2. Если область допустимых решений задачи является выпуклой многогранной областью, то оптимальное решение задачи либо не существует, либо существует и достигается, по крайней мере, в одной из угловых точек области.
Можно доказать, что каждой угловой точке выпуклого многогранника или выпуклой многогранной области соответствует взаимно однозначным образом опорное (базисное неотрицательное) решение эквивалентной системы уравнений.
Если оптимальное решение достигается более чем в одной угловой точке, то оно достигается в любой точке, являющейся выпуклой линейной комбинацией этих угловых точек, т.е. если эти угловые точки обозначить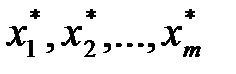 
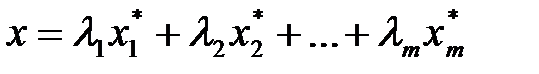
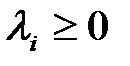
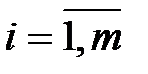
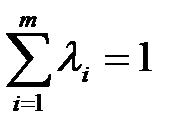
, то оптимальное решение достигается в любой точке
, где 
( 
), 
.
Основной вывод. Если задача линейного программирования имеет оптимальное решение, то оно совпадает, по крайней мере, с одним из опорных решений системы ограничительных уравнений.
Указанные свойства позволят в дальнейшем наметить общие методы решения таких задач.
Симплексный метод (с. м.) является одним из основных способов практического решения задач линейного программирования. Большинство широко распространенных программных средств, позволяющих решать задачи л. п., используют алгоритмы симплексного метода.
ПРИМЕР. Решить задачу л. п. симплексным методом: 
Нам будет удобно привести данную задачу к каноническому виду следующим образом. Введем новую дополнительную переменную y1 такую, что будет выполняться равенство -x1+3x2+y1=3. При этом, очевидно, y1³0. Аналогично, для любых x1, x2, x3, удовлетворяющих второму неравенству системы, существует переменная y2³0 такая, что 2x1 — 2x2 + 2x3 + y2=1, и, наконец, существует y3³0, что — x1+4x2-2x3+y3= 0 для x1, x2, x3, удовлетворяющих третьему неравенству системы. Таким образом, исходная задача эквивалентна следующей:
Разрешим систему уравнений относительно введенных нами переменных y1, y2, y3 и запишем ее в виде удобном для применения м.ж.и. :
Напомним, что переменные, относительно которых система разрешена (в нашем случае это y1, y2, y3), называются базисными, а остальные — свободными. Если свободные переменные приравняем нулю, то получим базисное решение. В нашем случае оно будет выглядеть так :
Базисное решение , в котором все базисные переменные принимают неотрицательные значения, называется опорным решением. Таким образом, это опорное решение системы . Запишем систему и целевую функцию z в таблицу1. Такая таблица называется симплексной.
| Б / С | -х1 | -х2 | -х3 |
| У1 | -1 | ||
| У2 | -2 | ||
| У3 | -1 | -2 | |
| z | -2 | -3 |
Здесь коэффициенты из каждой строки умножаются на соответствующие заголовки. Таким образом, из таблицы
z = — 2 ( — x1 ) + 4 ( — x2 ) — 3 ( — x3 ) + 2 * 1 или
z = 2x1 — 4x2 + 3x3 + 2 , то есть целевая функция записана в таблицу верно.
Теперь мы будем перебирать одно за другим базисные решения, пока не получим оптимальный план или не убедимся в неразрешимости рассматриваемой задачи.
На данном примере рассмотрим алгоритм перехода от опорного плана к оптимальному.
Для того чтобы найти новое базисное решение, достаточно выбрать разрешающий столбец и разрешающую строку.
Разрешающий столбец будем выбирать по наименьшему отрицательному элементу z — строки, кроме свободного члена. Выбранный столбец будем отмечать стрелкой . (В таблице 1 это столбец ( — x3 ).)
Для того чтобы выбрать разрешающую строку, разделим свободный член каждой строчки на элемент этой же строки, находящийся в выбранном столбце. Получаем в первой строке 3/3; во второй строке — 1/2 ; в третьей строке — 0 / (-2). Полученное таким образом отношение назовем симплексным отношением ( с. о. ), если оно больше нуля или имеет вид 0/a , где a > 0. В нашем случае 3/3 и 1/2 — симплексные отношения, а 0/(-2) не является симплексным отношением. Разрешающую строку будем выбирать по наименьшему симплексному отношению разрешающего столбца. В нашем примере надо выбрать вторую строку, так как 1/2
Источник
