- Сервис для решения задач по линейному программированию
- Пример №2. Решение задачи линейного программирования графическим методом. Функция достигает наименьшего значения в точке
- x1 = 1
- x2 = 3/2
- F min = 5
- 2.3. Графический метод решения задачи линейного программирования
- Сервис для решения задач по линейному программированию
- Пример №2. Решение задачи линейного программирования графическим методом. Функция достигает наименьшего значения в точке
- x1 = 1
- x2 = 3/2
- F min = 5
Сервис для решения задач по линейному программированию
и другие интересные типовые задачи
Пример №2. Решение задачи линейного программирования графическим методом.
Функция достигает наименьшего значения в точке
при следующих ограничениях:
 | x1 | + | 2 x2 | ≤ | 8 |
| x1 | — | x2 | ≤ | 2 | |
| x1 | + | 2 x2 | ≥ | 4 | |
| x1 | ≥ | 1 |
x1 ≥ 0 x2 ≥ 0
Точки, координаты которых удовлетворяют одновременно всем неравенствам системы ограничений, называются областью допустимых решений.
Очевидно, для нахождения области допустимых решений данной задачи, необходимо последовательно рассмотреть каждое неравенство. (см. шаг 1 — шаг 4)
Последние два шага служат непосредственно для получения ответа. (см. шаг 5 — шаг 6)
Это стандартная схема решения. Если область допустимых решений представляет собой точку или пустое множество, то решение будет короче.
По условию задачи: x1 ≥ 0 x2 ≥ 0.
Если бы это было единственным условием, то область допустимых решений имела бы вид, как на рисунке (вся первая четверть).
Рассмотрим неравенство 1 системы ограничений.
Построим прямую: x1 + 2 x2 = 8
Найдены коородинаты двух точек (0, 4) и (8 ,0). Соединяем их и получаем необходимую прямую (1).
Нас интересуют точки расположенные выше или ниже построенной прямой (1) ?
Вернемся к исходному неравенству.
Преобразуем неравенство, оставив в левой части только x2
Знак неравенства ≤ . Следовательно, нас интересуют точки расположенные ниже построенной прямой (1).
Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.
Рассмотрим неравенство 2 системы ограничений.
Найдены коородинаты двух точек (0, -2) и (2 ,0). Соединяем их и получаем необходимую прямую (2).
Нас интересуют точки расположенные выше или ниже построенной прямой (2) ?
Вернемся к исходному неравенству.
Преобразуем неравенство, оставив в левой части только x2
Знак неравенства ≥ . Следовательно, нас интересуют точки расположенные выше построенной прямой (2).
Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.
Рассмотрим неравенство 3 системы ограничений.
Построим прямую: x1 + 2 x2 = 4
Найдены коородинаты двух точек (0, 2) и (4 ,0). Соединяем их и получаем необходимую прямую (3).
Нас интересуют точки расположенные выше или ниже построенной прямой (3) ?
Вернемся к исходному неравенству.
Преобразуем неравенство, оставив в левой части только x2
Знак неравенства ≥ . Следовательно, нас интересуют точки расположенные выше построенной прямой (3).
Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.
Рассмотрим неравенство 4 системы ограничений.
Построим прямую: x1 = 1
Данная прямая параллельна оси OX2 и проходит через точку (1,0) (4)
Знак неравенства ≥ . Следовательно, нас интересуют точки расположенные правее построенной прямой (4).
Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.
Строим вектор C = (2, 2), координатами которого являются коэффициенты функции F.
Будем перемещать «красную» прямую, перпендикулярно вектору C , от левого нижнего угла к правому верхнему.
В точке, в которой «красная» прямая в первый раз пересечет область допустимых решений, функция F достигает своего наименьшего значения.
В точке, в которой «красная» прямая в последний раз пересечет область допустимых решений, функция F достигает своего наибольшего значения.
Функция F достигает наименьшего значения в точке A. (см. рисунок)
Найдем координаты точки A.
Точка A одновременно принадлежит прямым (3) и (4).
| x1 | + | 2 x2 | = | 4 | => | x1 = 1 |
| x1 | = | 1 | x2 = 3/2 |
Вычислим значение функции F в точке A (1,3/2).
F (A) = 2 * 1 + 2 * 3/2 = 5
x1 = 1
x2 = 3/2
F min = 5
Замечание: если возникли сомнения, что функция F достигает своего минимума в точке А, необходимо найти значение функции в интересующей точке и сравнить с F(A).
Источник
2.3. Графический метод решения задачи линейного программирования
Если число переменных в задаче линейного программирования (ЗЛП) равно двум, а ограничениями является система неравенств, то задачу можно решать графическим методом.
При продаже двух видов товара используется 4 типа ресурсов. Норма затрат ресурсов на реализацию единицы товара, общий объем каждого ресурса заданы в табл. 2.3.1.
Норма затрат ресурсов на товары
Прибыль от реализации одной единицы товара первого вида составляет 2 усл. ед., второго вида – 3 усл. ед.
Требуется найти оптимальный план реализации товаров, обеспечивающий торговому предприятию максимальную прибыль.
Это задача составления плана реализации товара (пример 2.2.5) при 
=2,
=4.
Математическая модель имеет вид
(2.3.1)
(2.3.2)
В модели управляющие переменные 
,
– количество реализуемых изделий первого и второго вида, соответственно,
– прибыль. Система неравенств включает ограничения по ресурсам. Количество ресурсов на реализацию товаров первого и второго вида не превышает общего количества ресурсов каждого типа.
Построим в плоскости 
область допустимых решений. Каждое неравенство системы (2.3.2) определяет в плоскости 
полуплоскость, лежащую выше или ниже прямой, определяемой соответствующим уравнением. Построим прямые
Рассмотрим точку с координатами 
. Подставив их в первое неравенство, получаем
– верно, следовательно, искомая полуплоскость лежит ниже прямой
; остальные полуплоскости находятся аналогичным образом.
Область 
– область решения задачи.
Для нахождения максимального значения 
проверим граничные точки из области решений.
Построим две линии уровня:
Функция 
возрастает в направлении вектора-нормали
, следовательно, минимум находится в точке (0;0). Максимум определяем, передвигая нашу линию уровня в направлении вектора
параллельно самой себе до тех пор, пока хотя бы одна ее точка будет принадлежать области допустимых решений.
В данном случае это точка: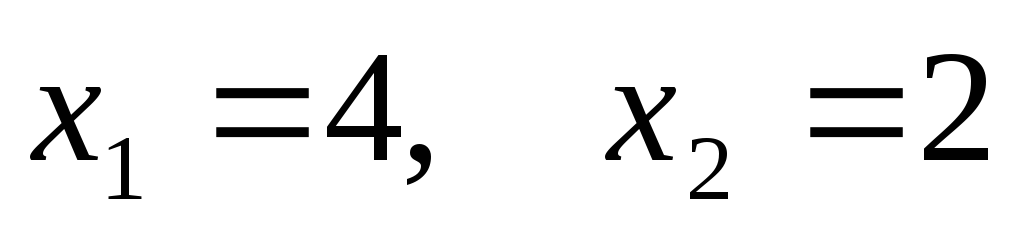 
;
при этом 
.
Таким образом, для получения максимальной прибыли в размере 14 усл. ед. надо продать 4 изделия первого вида и 2 изделия второго вида.
Изложенный выше графический метод применим для решения задач линейного программирования следующего вида:
(2.3.3)
(2.3.4)
Алгоритм решения ЗЛП графическим методом.
Записывают уравнения прямых, соответствующих ограничениям (2.3.4), и строят их на плоскости 
.
2) Определяют области, в которых выполняются ограничения задачи. Для этого выбирают произвольную точку на плоскости 
и подставляют ее координаты в первую часть одного из неравенств. Если неравенство верно, то искомая полуплоскость находится с той же стороны от прямой, что и точка; в противном случае искомая полуплоскость лежит с противоположной стороны от прямой. Эти действия последовательно выполняются для всех неравенств (2.3.4).
Определяют область допустимых решений задачи как область пересечения 
полуплоскостей, соответствующих 
ограничениям задачи.
Определяют направление возрастания (убывания) целевой функции 
.Это можно сделать двумя способами. Можно построить вектор-нормаль
, его направление показывает направление возрастания функции
, в противоположном направлении функция убывает. Можно просто построить две линии уровня функции
; 
; (
) –произвольные константы, 
), и по их расположению определить направление возрастания (убывания) функции.
Определяют граничную точку (точки) области допустимых решений, в которых целевая функция принимает максимальное или минимальное значение.
Вычисляют значения найденной точки, решая совместно уравнения, задающие прямые, на пересечении которых находится эта точка, или выявляя уравнение граничной прямой области допустимых решений, с которой совпадает линия уровня целевой функции.
Возможны следующие варианты области допустимых решений (рис. 2.3.2 – рис. 2.3.5):
На рис. 2.3.2, 2.3.3 показаны варианты пересечения линии уровня целевой функции с областью допустимых решений. Может быть единственное решение – точка В, бесконечно много решений – отрезок CD (рис.2.3.2), максимальным (минимальным) значением целевой функции может быть 
(рис.2.3.3).
После изучения данного раздела целесообразно решить задачу 1 контрольной работы № 3.
Источник
Сервис для решения задач по линейному программированию
и другие интересные типовые задачи
Пример №2. Решение задачи линейного программирования графическим методом.
Функция достигает наименьшего значения в точке
при следующих ограничениях:
| x1 | + | 2 x2 | ≤ | 8 |
| x1 | — | x2 | ≤ | 2 | |
| x1 | + | 2 x2 | ≥ | 4 | |
| x1 | ≥ | 1 |
x1 ≥ 0 x2 ≥ 0
Точки, координаты которых удовлетворяют одновременно всем неравенствам системы ограничений, называются областью допустимых решений.
Очевидно, для нахождения области допустимых решений данной задачи, необходимо последовательно рассмотреть каждое неравенство. (см. шаг 1 — шаг 4)
Последние два шага служат непосредственно для получения ответа. (см. шаг 5 — шаг 6)
Это стандартная схема решения. Если область допустимых решений представляет собой точку или пустое множество, то решение будет короче.
По условию задачи: x1 ≥ 0 x2 ≥ 0.
Если бы это было единственным условием, то область допустимых решений имела бы вид, как на рисунке (вся первая четверть).
Рассмотрим неравенство 1 системы ограничений.
Построим прямую: x1 + 2 x2 = 8
Найдены коородинаты двух точек (0, 4) и (8 ,0). Соединяем их и получаем необходимую прямую (1).
Нас интересуют точки расположенные выше или ниже построенной прямой (1) ?
Вернемся к исходному неравенству.
Преобразуем неравенство, оставив в левой части только x2
Знак неравенства ≤ . Следовательно, нас интересуют точки расположенные ниже построенной прямой (1).
Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.
Рассмотрим неравенство 2 системы ограничений.
Найдены коородинаты двух точек (0, -2) и (2 ,0). Соединяем их и получаем необходимую прямую (2).
Нас интересуют точки расположенные выше или ниже построенной прямой (2) ?
Вернемся к исходному неравенству.
Преобразуем неравенство, оставив в левой части только x2
Знак неравенства ≥ . Следовательно, нас интересуют точки расположенные выше построенной прямой (2).
Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.
Рассмотрим неравенство 3 системы ограничений.
Построим прямую: x1 + 2 x2 = 4
Найдены коородинаты двух точек (0, 2) и (4 ,0). Соединяем их и получаем необходимую прямую (3).
Нас интересуют точки расположенные выше или ниже построенной прямой (3) ?
Вернемся к исходному неравенству.
Преобразуем неравенство, оставив в левой части только x2
Знак неравенства ≥ . Следовательно, нас интересуют точки расположенные выше построенной прямой (3).
Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.
Рассмотрим неравенство 4 системы ограничений.
Построим прямую: x1 = 1
Данная прямая параллельна оси OX2 и проходит через точку (1,0) (4)
Знак неравенства ≥ . Следовательно, нас интересуют точки расположенные правее построенной прямой (4).
Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.
Строим вектор C = (2, 2), координатами которого являются коэффициенты функции F.
Будем перемещать «красную» прямую, перпендикулярно вектору C , от левого нижнего угла к правому верхнему.
В точке, в которой «красная» прямая в первый раз пересечет область допустимых решений, функция F достигает своего наименьшего значения.
В точке, в которой «красная» прямая в последний раз пересечет область допустимых решений, функция F достигает своего наибольшего значения.
Функция F достигает наименьшего значения в точке A. (см. рисунок)
Найдем координаты точки A.
Точка A одновременно принадлежит прямым (3) и (4).
| x1 | + | 2 x2 | = | 4 | => | x1 = 1 |
| x1 | = | 1 | x2 = 3/2 |
Вычислим значение функции F в точке A (1,3/2).
F (A) = 2 * 1 + 2 * 3/2 = 5
x1 = 1
x2 = 3/2
F min = 5
Замечание: если возникли сомнения, что функция F достигает своего минимума в точке А, необходимо найти значение функции в интересующей точке и сравнить с F(A).
Источник
