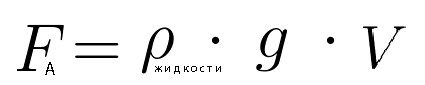Тема урока «Задача Архимеда»
Статья посвящена лемме Архимеда о перпендикулярных хордах. Как передать красоту этой задачи? Разнообразие способов ее решения? Эмоции, которые она вызывает у тех, кто любит геометрию? Может быть, об этом лучше расскажет урок, который прошел в 9-м математическом классе у одного из авторов. Если так, то давайте приоткроем дверь и проникнем на урок, урок эрудиции, знаний и творчества учащихся. И называться он будет так: «Урок одной задачи. »
Хорды AB и CD окружности радиуса R перпендикулярны и делятся точкой пересечения на отрезки a, b, c, d (рис. 1). Докажите, что сумма квадратов этих отрезков есть величина постоянная для данной окружности, равная квадрату ее диаметра, то есть
Да, задача хороша на слух, красива на вид и вызывает интерес у учащихся. Но стоит ли посвящать урок одной задаче?
Безусловно стоит! Потому что эта задача:
1) задача Архимеда, позволяющая понять его гениальность;
2) она — конкурсная, во многих вузах ее предлагают на вступительных экзаменах;
3) она позволяет повторить ряд важнейших фактов и задач планиметрии;
4) она трудная! (Даже искушенные в геометрии ученики не сразу справляются с ней.);
5) она решается удивительно красиво и изящно и разными способами.
Знакомство с задачей Архимеда происходит на предыдущем уроке. Дома ученики решают эту задачу, но возможно большим числом способов!
Однако задача непростая, и удастся ли большей части класса вообще решить ее?
Перед уроком две минуты говорю с ребятами о задаче, бегло просматриваю их решения. В это время звенит звонок, и я начинаю Урок одной задачи.
Прошу выйти к доске Федора, потому что до урока заметил, что его решение совпадает с решением Архимеда. (Представляется важным начать именно с авторского решения.) Он рассказывает.
Решение 1. Пусть a, b, c, d — данные отрезки хорд AB и CD (рис. 2). Пусть AD = x, CB = y. Тогда по теореме Пифагора для треугольника AED:
А по теореме Пифагора для треугольника BEC:
Проведем AK 

Здесь я останавливаю Федора и прошу другого ученика продолжить рассказ.
CKAD — равнобокая трапеция, поскольку только равнобокую можно вписать в окружность, и CK = AD = x. 
Воспользовавшись равенствами (1) и (2), получаем требуемое:
— У меня решение, которое Архимед не мог предложить! — включается в разговор Юля. — Ведь тригонометрия появилась значительно позже.
Юля идет к доске и показывает свой способ решения.
Решение 2. К тем же обозначениям (см. рис. 1 и 2) добавим следующие (рис. 3): (из прямоугольного треугольника AEC). Тогда по теореме синусов для треугольника CAB:
А для треугольника ACD по той же теореме.
Здесь я прерываю рассказ и предлагаю самостоятельную работу: закончить решение задачи Архимеда способом, предложенным Юлей. (Ей в это время предлагаю подумать над еще одним, чисто геометрическим, способом решения задачи.)
Большинство учащихся успешно заканчивают задачу и сдают листки с решением.
Один из учеников показывает окончание решения на доске.
Решение 2 (продолжение). Для треугольника ACD по теореме синусов имеем:
Возведем обе части равенств (3) и (4) в квадрат и сложим:
x 2 + y 2 = 4R 2 (sin 2 α + cos 2 α) = 4R 2 .
С учетом (1) и (2), задача решена:
— Ребята, есть ли у кого другие способы решения задачи Архимеда?
— Я воспользовался симметрией при решении задачи, — говорит Женя. — А также известным свойством угла с вершиной внутри круга.
Женя идет к доске и записывает это свойство (рис. 4).
Затем начинает объяснять свой способ.
Решение 3. Согласно свойству угла с вершиной внутри круга полусумма дуг AD и BC равна 90° (рис. 5).


Проведем прямую l, содержащую диаметр, так что l 
Тогда и дуга DK равна BC (равные хорды стягиваются равными дугами). Значит,


Если это так, то AK — диаметр, и 
По теореме Пифагора для треугольника ADK x 2 + y 2 = 4R 2 , что равносильно решению задачи.
— У меня тоже симметрия, только немного по-другому! — выходит к доске Сергей и показывает.
Решение 4. Построим отрезок TK, симметричный AB относительно центра окружности O (рис. 6). В силу симметрии: TK = AB, CP = ED = d,
PK = BE = b. Очевидно, что PD = c. Из прямоугольного треугольника DPK имеем:
Очевидно, что AK — диаметр (так как ABKT — прямоугольник), и тогда 
— В этом способе возможно другое решение! — берет слово Наташа.
Решение 5. Воспользуемся тем же рисунком (рис. 6).

Тогда AK 2 = AB 2 + BK 2 , или:
Но по известной теореме о равенстве произведений отрезков хорд ab = cd. Тогда 2ab и –2cd сократятся! Решение задачи получено.
— А у меня принципиально другое решение, не похожее ни на одно из предыдущих! — заявляет Аленка.
Перед уроком я бегло просмотрел способ Аленки. Обращаюсь к классу:
— Если способ верен, то это — маленькая сенсация. Такого способа решения задачи Архимеда я нигде в литературе не встречал.
Решение 6. Проведем в треугольнике ABC высоту AK (рис. 7). Тогда H — ортоцентр (точка пересечения высот) треугольника ABC. Покажем, что AH = AD = x. Действительно, (вписанные, опирающиеся на одну дугу). Тогда из треугольника ABK:


Далее применим хорошо известную формулу:
Здесь я прерываю рассказ и предлагаю ученикам самостоятельно завершить решение задачи (мне уже понятно, что сенсация состоялась). Попутно спрашиваю у учащихся доказательство предложенной Аленкой формулы (6).
Знание формулы входит в их эрудицию, и мне предлагается несколько способов доказательства.
Большинство учеников легко разгадывают и дальнейший ход рассуждений в решении 6.
Решение 6 (продолжение).
то есть x 2 + y 2 = 4R 2 .
Ну что ж, такого способа учитель не знал!
Формула (6) подсказывает Антону идею, которая дарит нам еще один способ решения задачи. Он воспользовался известным ученикам свойством ортоцентра H: «Точки, симметричные ортоцентру относительно сторон треугольника, принадлежат описанной окружности».
На рисунке 8 точки H и H’ симметричны друг другу относительно стороны BC.
Этот факт предлагаем читателям доказать самостоятельно!
С учетом вышесказанного, способ Антона выглядит так (хорда CD опущена вниз для удобства работы с рис. 9):
Решение 7.
Но ab = cd — из равенства произведений отрезков хорд. Тогда
В заключение урока — маленький сюрприз от Данила. Я попросил его выполнить векторное решение задачи Архимеда, придуманное одним из наших выпускников несколько лет назад.
Докажем, что α + β = 180°: 

Тогда β = 180° –α и cos β = –cos α, откуда следует, что
Задача Архимеда решена еще одним, векторным способом!
Подводим итоги «Урока одной задачи»:
- повторены важнейшие факты планиметрии;
- предложено много способов решения знаменитой задачи;
- задача решена векторным способом.
К домашнему заданию, которое написано на доске, добавлю: решить задачу Архимеда методом координат. Такое решение существует!
Итак, «Урок одной задачи» состоялся. Осуществилась связь времен, связь прошлого с настоящим.
Источник
Задача архимеда способы решения
Репетитор
по физике
На тело, погруженное в жидкость действует вверх сила, равная весу вытесненной жидкости.
\(\rho\) это плотность жидкости или газа, то есть той среды, в которой находится тело
Силу Архимеда еще называют выталкивающей силой.
0. Аня уронила в речку мячик объёмом 0,8 л какая сила архимеда действует на мячик,если он погружен в воду только наполовину?
Показать ответ Показать решение Видеорешение
\(F_A=1000\dfrac<КГ><М^3>\cdot 10\dfrac<Н> <КГ>\cdot \dfrac<1> <2>\cdot 0,0008м^3=4Н \)
Репетитор по физике
1. Найти силу Архимеда, действующую на тело объемом \(V=150 см^3\), целиком погруженное в воду .Плотность воды: \(\rho=1000\dfrac<кг><м^3>\).
Показать ответ Показать решение Видеорешение
2. Найти силу Архимеда, действующую на тело объемом \(V=850 см^3\), целиком погруженное в керосин .Плотность керосина \(\rho=800\dfrac<кг><м^3>\)
Показать ответ Показать решение Видеорешение
3. Найти силу Архимеда, действующую на тело объемом \(V=2 м^3\), половина объема которого погружено в воду .Плотность воды: \(\rho=1000\dfrac<кг><м^3>\)
Показать ответ Показать решение Видеорешение
Сила Архимеда зависит только от той части объема, который погружен в жидкость, поэтому мы берем половину объема
4. Найти силу Архимеда, действующую на тело объемом \(V=2 м^3\), четверть объема которого погружено в воду .Плотность воды: \(\rho=1000\dfrac<кг><м^3>\)
Сила Архимеда зависит только от той части объема, который погружен в жидкость, поэтому мы берем одну четвертую объема \(V=\dfrac<1><4>\cdot 2 м^3 \: =0,5 м^3 \)
5. Найти объем тела, полностью погруженного в воду, если действующая на него сила Архимеда \(F_A=20\) Н , а плотность воды \(\rho=1000 \) \(\dfrac<КГ><М^3>\)
6. На тело, объемом \(V=0,5м^3\) полностью погруженное в жидкость, действуюет сила Архимеда \(F_A=5000Н\). Найти плотность этой жидкости.
Показать ответ Показать решение Видеорешение
7. Стальной шар объемом \(V=50см^3\), полностью погружен в воду. Какая сила Архимеда действует на шар? Плотность воды \(\rho=1000\dfrac<кг><м^3>\)
Показать ответ Показать решение Видеорешение
8. Чему равна выталкивающая сила (сила Архимеда), действующая в воде на полностью погруженный железный шар массой 0,78 кг? Плотность воды \(\rho_в=1000\dfrac<кг><м^3>\) , Плотность железа \(\rho_ж=7800\dfrac<кг><м^3>\)
Показать ответ Показать решение Видеорешение
\(F_A=\rho_в\cdot g \cdot V\)
9. Чему равна выталкивающая сила, действующая в воде на полностью погруженный деревянный брусок размером 60x10x15см? Плотность воды \(\rho_в=1000\dfrac<кг><м^3>\)
Показать ответ Показать решение Видеорешение
\(F_A=1000\dfrac<кг><м^3>\cdot 10\dfrac<Н> <кг>\cdot 0,6м \cdot 0,1м \cdot 0,15м \: = \: 90 Н \)
10. Чему равна сила Архимеда, действующая в бензине на полностью погруженный медный брусок размером 6x1x2см? Плотность бензина \(\rho_в=710\dfrac<кг><м^3>\)
Показать ответ Показать решение Видеорешение
\(F_A=710\dfrac<кг><м^3>\cdot 10\dfrac<Н> <кг>\cdot 0,06м \cdot 0,01м \cdot 0,02м \: = \: 0,0852 Н \)
11. Чему равна архимедова сила, действующая в воздухе на шарик объемом \(V=3000 см^3\)? Плотность воздуха \(\rho_в=1,29\dfrac<кг><м^3>\)
Показать ответ Показать решение Видеорешение
\(F_A=1,29\dfrac<кг><м^3>\cdot 10\dfrac<Н> <кг>\cdot 0,003м^3 \: = \: 0,0387 Н \)
12. Какую силу нужно приложить к камню, находящемуся под водой, чтобы не дать ему пойти ко дну, если на него действует сила тяжести \(F_Т=10Н\) и сила Архимеда \(F_A=4Н\)?
Куда направлена эта сила?
Показать ответ Показать решение Видеорешение
Камень, находящийся под водой, утонет(будет двигаться вниз), если не прикладывать к нему внешней силы, поэтому внешняя сила направлена вверх
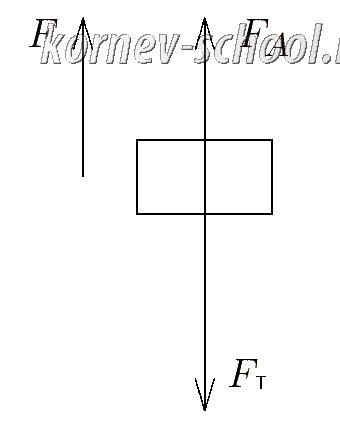
Составим уравнение балланса сил (с 9 класса оно называется первым законом Ньютона )
Сумма сил, направленных вверх равна сумме сил направленных вниз
13. Какую силу нужно приложить к стальному предмету, находящемуся под водой, чтобы не дать ему пойти ко дну, если на него действует сила тяжести \(F_Т=780Н\) и сила Архимеда \(F_A=100Н\)?
Куда направлена эта сила?
Предмет, находящийся под водой, утонет(будет двигаться вниз), если не прикладывать к нему внешней силы, поэтому внешняя сила направлена вверх

Составим уравнение балланса сил (с 9 класса оно называется первым законом Ньютона )
Сумма сил, направленных вверх равна сумме сил направленных вниз
14. Какую силу нужно приложить к деревянному предмету, находящемуся под водой, чтобы не дать ему всплывать, если на него действует сила тяжести \(F_Т=50Н\) и сила Архимеда \(F_A=125Н\)?
Куда направлена эта сила?
Показать ответ Показать решение Видеорешение
Без приложения внешней силы предмет будет всплывать вверх, а чтобы не давать ему всплывать нужно приложить силу, направленную вниз
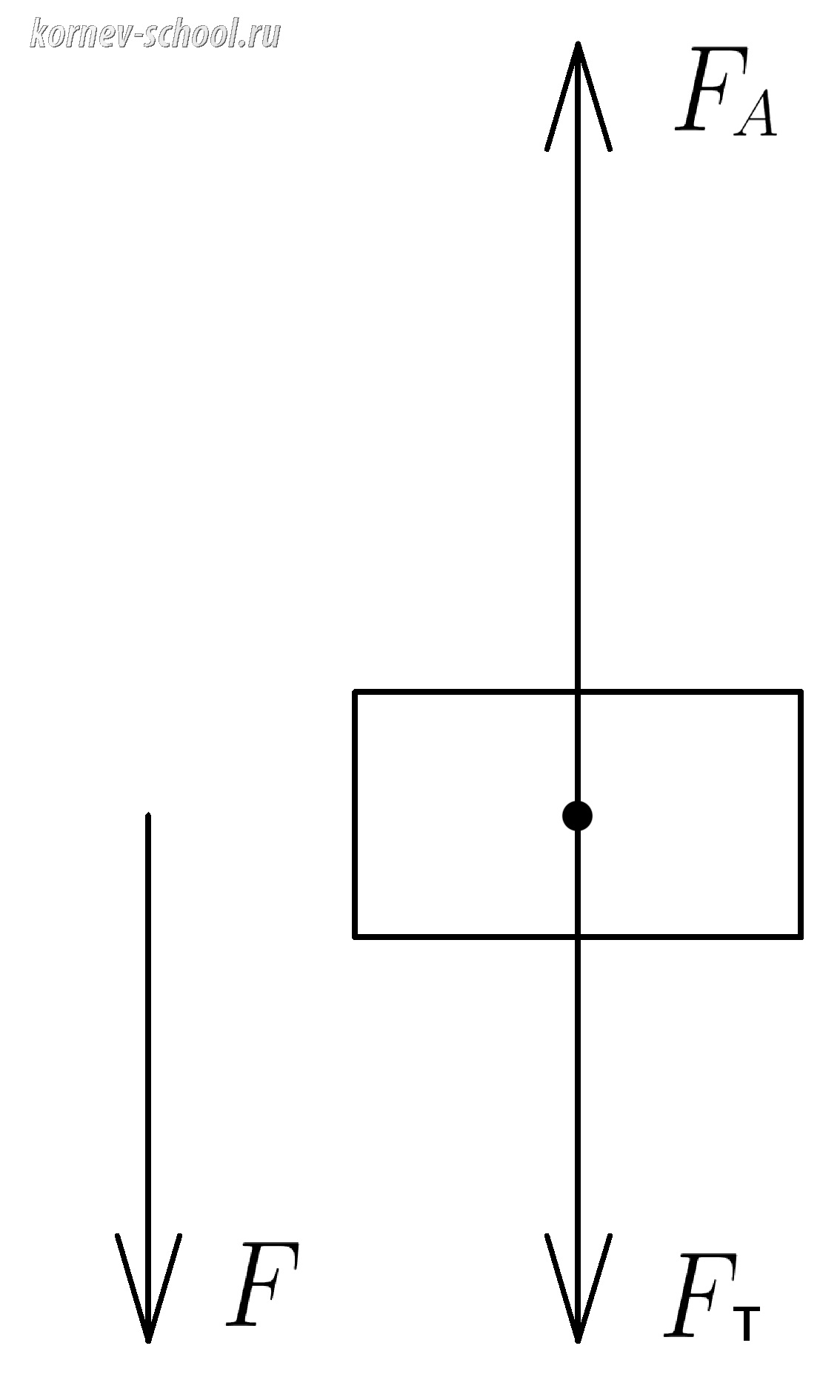
Составим уравнение балланса сил (с 9 класса оно называется первым законом Ньютона )
Сумма сил, направленных вверх равна сумме сил направленных вниз
15. Какую силу нужно приложить к деревянному бруску, объемом \(V= 0,1 м^3\), находящемуся под водой, чтобы не давать ему всплывать ?
Плотность воды \(\rho_в=1000\dfrac<кг><м^3>\). Плотность дерева \(\rho_д=400\dfrac<кг><м^3>\)
Без приложения внешней силы деревянный брусок будет всплывать вверх, а чтобы не давать ему всплывать нужно приложить силу, направленную вниз

Составим уравнение балланса сил (с 9 класса оно называется первым законом Ньютона )
Сумма сил, направленных вверх равна сумме сил направленных вниз
\( F= \rho_в \cdot g \cdot V-m \cdot g= \rho_в \cdot g \cdot V- \rho_д \cdot V \cdot g=gV(\rho_в-\rho_д) \)
\( F= 10\dfrac<Н> <кг>\cdot 0,1 м^3 \cdot ( 1000\dfrac<кг> <м^3>— 400\dfrac<кг> <м^3>)=600 Н \)
16. Какую силу нужно приложить к деревянной доске, объемом \(V= 300 см^3\), находящейся под водой, чтобы не давать ей всплывать ?
Плотность воды \(\rho_в=1000\dfrac<кг><м^3>\). Плотность дерева \(\rho_д=400\dfrac<кг><м^3>\)
Без приложения внешней силы деревянная доска будет всплывать вверх, а чтобы не давать ей всплывать нужно приложить силу, направленную вниз

Составим уравнение балланса сил (с 9 класса оно называется первым законом Ньютона )
Сумма сил, направленных вверх равна сумме сил направленных вниз
\( F= \rho_в \cdot g \cdot V-m \cdot g= \rho_в \cdot g \cdot V- \rho_д \cdot V \cdot g=gV(\rho_в-\rho_д) \)
\( F= 10\dfrac<Н> <кг>\cdot 0,0003 м^3 \cdot ( 1000\dfrac<кг> <м^3>— 400\dfrac<кг> <м^3>)=1,8 Н \)
17. Какую силу нужно приложить к стальному листу, массой \(m= 780 г\), находящемуся под водой, чтобы не давать ему утонуть ?
Плотность воды \(\rho_в=1000\dfrac<кг><м^3>\). Плотность стали \(\rho_с=7800\dfrac<кг><м^3>\)
Без приложения внешней силы стальной лист будет будет тонуть (двигаться вниз), чтобы не давать ему тонуть нужно приложить силу, направленную вверх

Составим уравнение балланса сил (с 9 класса оно называется первым законом Ньютона )
Сумма сил, направленных вверх равна сумме сил направленных вниз
\( F= m \cdot g- \rho_в \cdot g \cdot V= m \cdot g-\rho_в \cdot g \cdot \dfrac
19. Какую силу нужно приложить к сплошному деревянному кубу, массой \(m= 3 кг\), находящемуся под водой, чтобы не давать ему всплывать ?
Плотность воды \(\rho_в=1000\dfrac<кг><м^3>\). Плотность дерева \(\rho_д=400\dfrac<кг><м^3>\)
Показать ответ Показать решение Видеорешение
20. Полый алюминиевый куб, массой \(m= 3 кг\) и объемом \(V= 0,01 м^3\) бросили в воду.
Плотность воды \(\rho_в=1000\dfrac<кг><м^3>\). Куб утонет или будет плавать на поверхности?
Показать ответ Показать решение Видеорешение
21. Полый алюминиевый куб, массой \(m_к= 3 кг\) и объемом \(V= 0,01 м^3\) бросили в воду, но едва он коснулся поверхности воды, как на него села птичка массой \(m_п= 2 кг\). Плотность воды \(\rho_в=1000\dfrac<кг><м^3>\). Удастся ли птичке поплавать на нем?
Показать ответ Показать решение Видеорешение
решение \(m_к=p 3 кг\) и \(\rho_в=1000\dfrac<кг><м^3>\)
22. Каким должен быть минимальный объем надувной лодки массой 50 кг, чтобы взять на борт груз массой 500 кг? Плотность воды \(\rho_в=1000\dfrac<кг><м^3>\). Удастся ли птичке поплавать на нем?
Показать ответ Показать решение Видеорешение
23. какая сила архимеда действует шар объемом \(1 м^3 \) и массой 0,5 кг плавающего на поверхности воды ?
Показать ответ Показать решение Видеорешение

В этой задаче дан полный объем шара, а в формуле силы Архимеда применяется тот объем, который находится под водой
Поэтому в этой задаче объем- лишнее данное
Сначала запишем условие плавания:
\( F_A= F_Т \)
\( F_A= m \cdot g=0,5 кг \cdot 10\dfrac<Н><кг>=5 Н \)
Источник