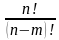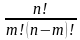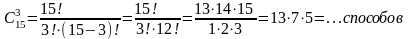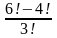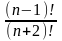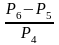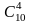За столом семь мест сколькими способами можно расставить семерых гостей

Практическая работа по теме : Размещения, сочетания, перестановки

Практическое занятие №8

Просмотр содержимого документа
«Практическая работа по теме : Размещения, сочетания, перестановки»

Практическое занятие Приложение 8

Размещения, сочетания и перестановки. История развития комбинаторики, теории вероятностей и статистики и их роль в различных сферах человеческой жизнедеятельности. Правила комбинаторики. Решение комбинаторных задач. Бином Ньютона и треугольник Паскаля. Прикладные задачи.

Произведение всех натуральных чисел от 1 до n включительно называют

n – факториалом и пишут .

n элементов n мест

порядок имеет значение

порядок имеет значение

порядок не имеет значение

=

= n (n – 1) (n – 2) … (n – m +1)

=

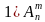
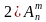
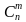
2) Подготовительный этап.

Перепишите и заполните пропуски:

Пример 1. За столом пять мест. Сколькими способами можно расставить пятерых гостей?

Решение: Р₅ = 5! = 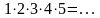_{способов}

Ответ: 120 способов.

Пример 2. а) Сколько трехзначных чисел можно записать, используя цифры 1,3,6,7,9, если каждая их них может быть использована в записи только один раз?

Решение: Искомое число вариантов равно числу размещений из 5 элементов по 3 элемента, т.е. по формуле получаем: 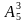= 5 4 3 = … чисел.

б) Из 20 студентов надо выбрать старосту, его заместителя и редактора газеты. Сколькими способами это можно сделать?

Решение: Искомое число вариантов равно числу размещений из 20 элементов по 3 элемента, т.е. по формуле получаем: 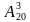= 20 19 18 = … способов.

Ответ: 6840 способов.

Пример 3. а) Из 15 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?

Решение: каждый выбор отличается от другого хотя бы одним дежурным. Значит, здесь речь идет о сочетаниях из 15 элементов по 3. Следовательно, по формуле получаем

Ответ: 455 способов.

б) Студентам дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами студент может выбрать из них 6 книг?

Решение: Выбор 6 из 10 без учёта порядка: 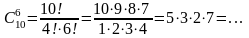способов.

Ответ: 210 способов.

3) Практический этап.

За столом семь мест. Сколькими способами можно расставить семерых гостей?

а) Сколько трехзначных чисел можно записать, используя цифры 1,2,4,6,7,9, если каждая их них может быть использована в записи только один раз?

б) Из 15 учащихся надо выбрать старосту, его заместителя и редактора газеты. Сколькими способами это можно сделать?

3. а) Из 25 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?

б) Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 7 книг?

Пример 4. Вычислить

Пример 5. Упростить

Пример 6. Вычислить

Пример 7. Вычислить ;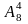

Источник

Самостоятельная работа по алгебре 10 класс на тему «Перестановки, сочетания, размещения»

Самостоятельная работа по предмету «Алгебра и начало аанализа» на тему «Перестановки, сочения, размещения».

Сколько мелодий можно сыграть из четырех различных нот? Воспользуйтесь правилом перестановки.

Сколькими способами можно случайным образом из 25 лучших студентов курса выбрать двух для поездки в Англию и Америку? Воспользуйтесь правилом размещения.

Сколько можно сыграть аккордов из четырех нот, выбранных из семи заданных различных нот? Воспользуйтесь правилом сочетания.

За столом семь мест. Сколькими способами можно расставить семерых гостей?

а) б) в)

Из 25 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?

Сколько можно составить четырех буквенных слов из букв слова «Брак»?

Воспользуйтесь правилом перестановки.

Сколько мелодий можно сыграть из четырех нот, выбранных без повторения из семи заданных различных нот? Воспользуйтесь правилом размещения.

Сколькими способами можно из группы в 25 человек случайным образом вызвать двух человек к доске? Воспользуйтесь правилом сочетания.

Сколько трехзначных чисел можно записать, используя цифры 1,2,4,6,7,9, если каждая из них может быть использована в записи только один раз?

а) б) в)

Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 7 книг?

Сколькими способами можно поставить 7 человек в очередь? Воспользуйтесь правилом перестановки.

На 9 карточках написано по одной цифре от 1 до 9 без повторения. Располагая любые три карточки в строку, мы получим трехзначное число. Сколько различных трехзначных числе можно получить при помощи этих 9 карточек? Воспользуйтесь правилом размещения.

Необходимо выбрать в подарок 4 из 10 имеющихся книг. Сколькими способами можно это сделать? Воспользуйтесь правилом сочетания.

Из 15 учащихся надо выбрать старосту, его заместителя и редактора газеты. Сколькими способами это можно сделать?

а) б) в)

Имеется 10 белых и 5 черных шаров. Сколькими способами можно выбрать 7 шаров, чтобы среди них были 3 черных?

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 812 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 286 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 599 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Международная дистанционная олимпиада Осень 2021

Похожие материалы

План урока по теме «Арифметическая прогрессия»

Индивидуальное домашнее задание «Рациональные дроби»

Презентация «Прямоугольная система координат»

Конспект урока «Числовая последовательность»

Открытый урок «Степень с натуральным показателем»

Конспект урока «Деление мнолгочленов » 2 урок»

Конспект урока «Деление многочленов»

КОМПЛЕКТ КОНТРОЛЬНО – ОЦЕНОЧНЫХ СРЕДСТВ ПО ДИСЦИПЛИНЕ

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5308427 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Руководители управлений образования ДФО пройдут переобучение в Москве

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Студентам вузов могут разрешить проходить практику у ИП

Время чтения: 1 минута

Правительство предложило потратить до 1 млрд рублей на установку флагов РФ у школ

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Презентация на тему «Комбинаторика»

Выбранный для просмотра документ Комбинаторика.pptx

Описание презентации по отдельным слайдам:

КОМБИНАТОРИКА Размещения, перестановки, сочетания

Произведение подряд идущих первых n натуральных чисел обозначают n! и называют «эн факториал»: Определение 1: n!=1·2·3·…·(n-2)·(n-1)·n

Теорема 1: n различных элементов можно расставить по одному на n различных мест ровно n! способами. Рn=n! — перестановки

6 слонят Сколькими способами можно их расставить? Например: 6!=1·2·3·4·5·6=720

Задача 1: К хозяину дома пришли гости A,B,C,D. За круглым столом – пять разных стульев. а) Сколькими способами можно рассадить гостей за столом? б) Сколькими способами можно рассадить гостей за столом, если место хозяина дома уже известно? A B C D хозяин

Решение: а) На 5 стульев должны сесть 5 человек (включая хозяина дома). Значит, всего имеется Р5 способов их рассаживания: Р5 =5!= 1·2·3·4·5= 120

Решение: б) Так как место хозяина фиксировано, то следует рассадить четырех гостей на четыре места. Это можно сделать Р4 способами: Р4 =4!= 1·2·3·4= 24

Задача 2: В чемпионате по футболу участвовало 7 команд. Каждая команда сыграла по одной игре с каждой командой. Сколько всего было игр?

Решение: Первый способ: Рассмотрим таблицу 7х7, в которой вписаны результаты игр. В ней 49 клеток: По диагонали клетки закрашены, т.к. никакая команда не играет сама с собой. Если убрать диагональные клетки, их останется 49-7=42. 1 2 3 4 5 6 7 1 3:1 0:5 2:2 0:0 1:0 1:3 2 4:3 1:0 1:0 0:0 1:1 3 1:3 1:0 1:2 0:0 4 1:1 1:1 1:4 5 1:0 0:0 6 2:2 7

Решение: В нижней части таблицы результатов нет, т.к. все они получаются отражением уже имеющихся результатов из верхней части таблицы. 3:1 1:3 Поэтому количество всех проведенных игр равно половине от 42, т.е. 21. 1 2 3 4 5 6 7 1 3:1 0:5 2:2 0:0 1:0 1:3 2 4:3 1:0 1:0 0:0 1:1 3 1:3 1:0 1:2 0:0 4 1:1 1:1 1:4 5 1:0 0:0 6 2:2 7

Второй способ: Произвольно пронумеруем команды №1, №2,…, №7 и посчитаем число игр поочередно. Команда №1 встречается с командами №2-7 – это 6 игр. Команда №2 тоже проведет 6 встреч, но одну игру , с командой №1, мы уже посчитали. Получается 5 новых игр. Команда №3 проведет 6 встреч, из которых две, с №1 и №2 мы посчитали, значит, добавится еще 4 игры. Продолжая, получим: 6 игр 5 игр 4 игры 3 игры 2 игры 1 игра 21 игра 6+5+4+3+2+1=21 1 2 3 4 5 6 7 1 3:1 0:5 2:2 0:0 1:0 1:3 2 4:3 1:0 1:0 0:0 1:1 3 1:3 1:0 1:2 0:0 4 1:1 1:1 1:4 5 1:0 0:0 6 2:2 7

Третий способ: Используем геометрическую модель: 7 команд – это вершины выпуклого семиугольника, а отрезок между двумя вершинами – это встреча двух соответствующих команд: сколько отрезков, столько игр. Из каждой вершины выходит 6 отрезков. Получается 7·6 отрезков, каждый из которых посчитан дважды: как АВ, так и ВА. Значит, всего проведен (7·6):2=42:2=21 отрезок. А В С D E F G

Выводы: Состав игры определен, как только мы выбираем две команды. Значит, количество всех игр в турнире для n команд – это количество всех выборов двух элементов из n данных элементов. При этом порядок выбора не важен.

Теорема 2: Если множество состоит из n элементов и требуется выбрать два элемента без учета их порядка, то такой выбор можно произвести способами.

Определение 2: Число всех выборов двух элементов без учета их порядка из n данных элементов называют числом сочетаний из n элементов по 2 и обозначают [«цэ из эн по два»]

Задача 3: Встретились 11 футболистов и 6 хоккеистов и каждый стал по одному разу играть с каждым в шашки, которые они «давненько не брали в руки». Сколько встреч было: а) между футболистами б) между хоккеистами в) всего?

А что получится, если мы будем учитывать порядок двух выбираемых элементов? Теорема 3: Если множество состоит из n элементов и требуется выбрать два элемента учитывая их порядок, то такой выбор можно произвести способами.

Определение 3: Число всех выборов двух элементов с учетом их порядка из n данных элементов называют числом размещений из n элементов по 2 и обозначают [«а из эн по два»]

Задача 4: В классе 27 учеников. К доске нужно вызвать двоих. Сколькими способами это можно сделать, если: а) первый ученик должен решить задачу по алгебре, а второй – по геометрии; б) они должны быстро стереть с доски? Решение: В случае а) порядок важен, а в случае б) – нет. Значит, а) б)

А как будут выглядеть формулы, если в них верхний индекс заменить на 5, 7, 10 и т.д.? Сколькими способами можно выбрать 5 учеников из 30 для дежурства в столовой; 7 монет из 10 данных; 10 карт из колоды в 32 карты? Определение 4: Число всех выборов k элементов из n данных без учета порядка называют числом сочетаний из n элементов по k и обозначают Число всех выборов k элементов из n данных с учетом их порядка называют числом размещений из n элементов по k и обозначают

Теорема 4: Для любых натуральных чисел n и k таких, что k 24 слайд

Задача 5: В классе 27 учеников, из них нужно выбрать троих. Сколькими способами это можно сделать, если: а) первый ученик должен решить задачу, второй – сходить за мелом, третий – пойти дежурить в столовую? б) им следует спеть в хоре?

Задача 6: «Проказница Мартышка, Осел, Козел и Косолапый Мишка затеяли сыграть квартет». Мишке поручили выбрать 4 любых инструмента из имеющихся 11. а) найти число всевозможных выборов инструментов; б) найти число всевозможных рассаживаний участников квартета с выбранными четырьмя инструментами (инструменты, как в басне Крылова, занимают четко отведенные позиции).

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 812 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 286 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 599 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: 37849032614

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Вопрос о QR-кодах для сотрудников школ пока не обсуждается

Время чтения: 2 минуты

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Руководители управлений образования ДФО пройдут переобучение в Москве

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Российские адвокаты бесплатно проконсультируют детей 19 ноября

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник