Умножение по-японски, или как легко и быстро перемножить числа без калькулятора
Как умножают в японии: Учимся считать с помощью линий.
В век смартфонов-калькуляторов и голосовых помощников умножение больших чисел вручную уже кажется необычным и совершенно ненужным навыком. Но жизнь – непредсказуемая штука: никогда не знаешь, когда понадобится быстро что-то посчитать. И в этом деле идеальным помощником будет японский метод умножения (иногда его называют умножением по строкам). Все, что вам понадобится, – лист бумаги и ручка. Чтобы облегчить задачу, вы можете использовать чернила разных цветов, но это вовсе необязательно.
Давайте рассмотрим, как работает этот метод.
Посчитаем, сколько будет 12 x 13.
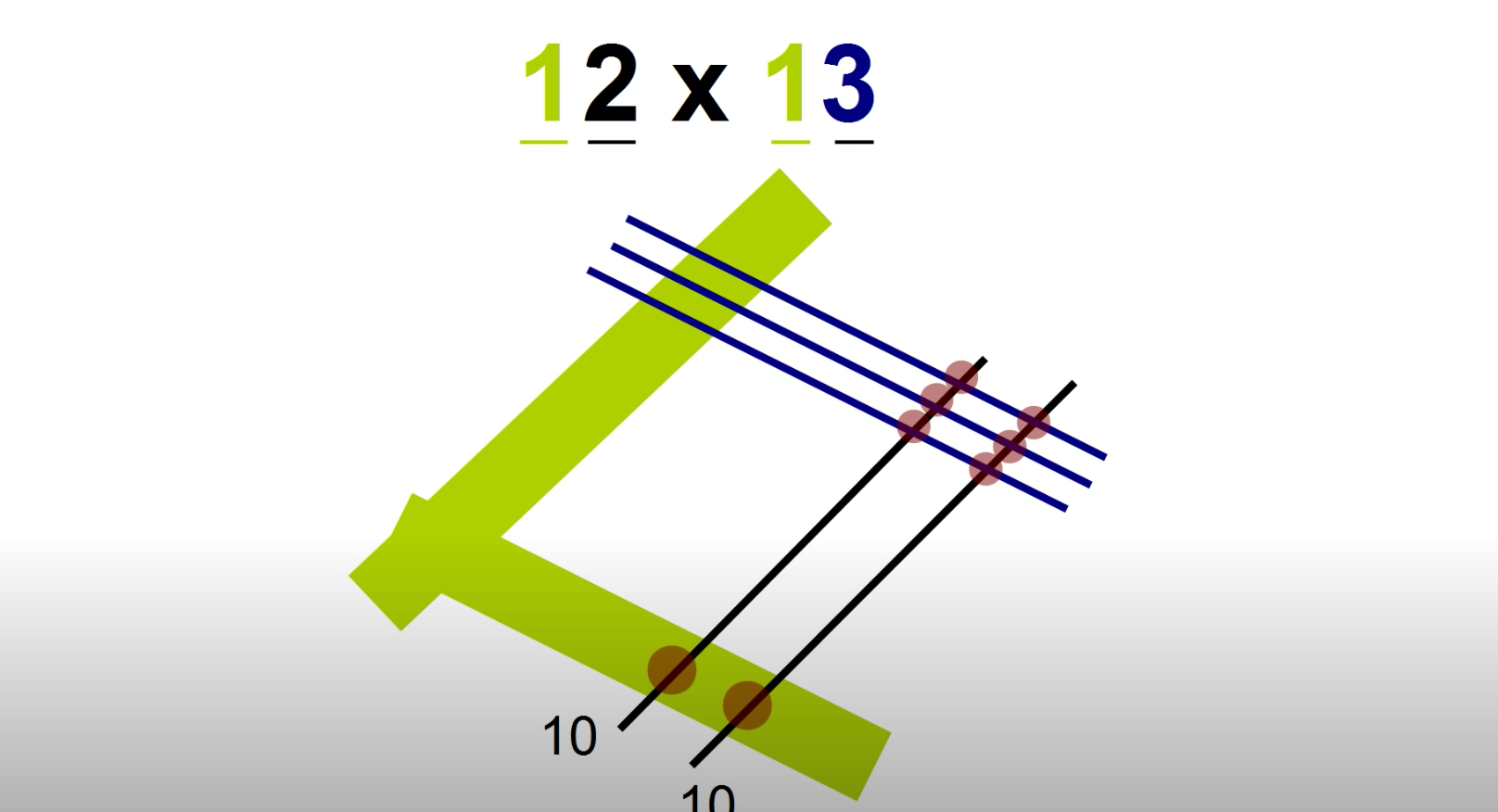
Первый шаг – рисуем линии. Один набор линий – для каждой «десятки» и параллельный набор – для разряда «единиц». У вас получится «квадрат», образованный одной линией для «десятков» числа 12 (зеленый цвет) + одной линией для «десятков» числа 13 (зеленый цвет) + двумя линиями для разряда «единиц» числа 12 (черный цвет) + тремя линиями для разряда «единиц» числа 13 (синий цвет). «Десятки» должны всегда располагаться слева, а прямоугольник – быть повернутым на 45 градусов.
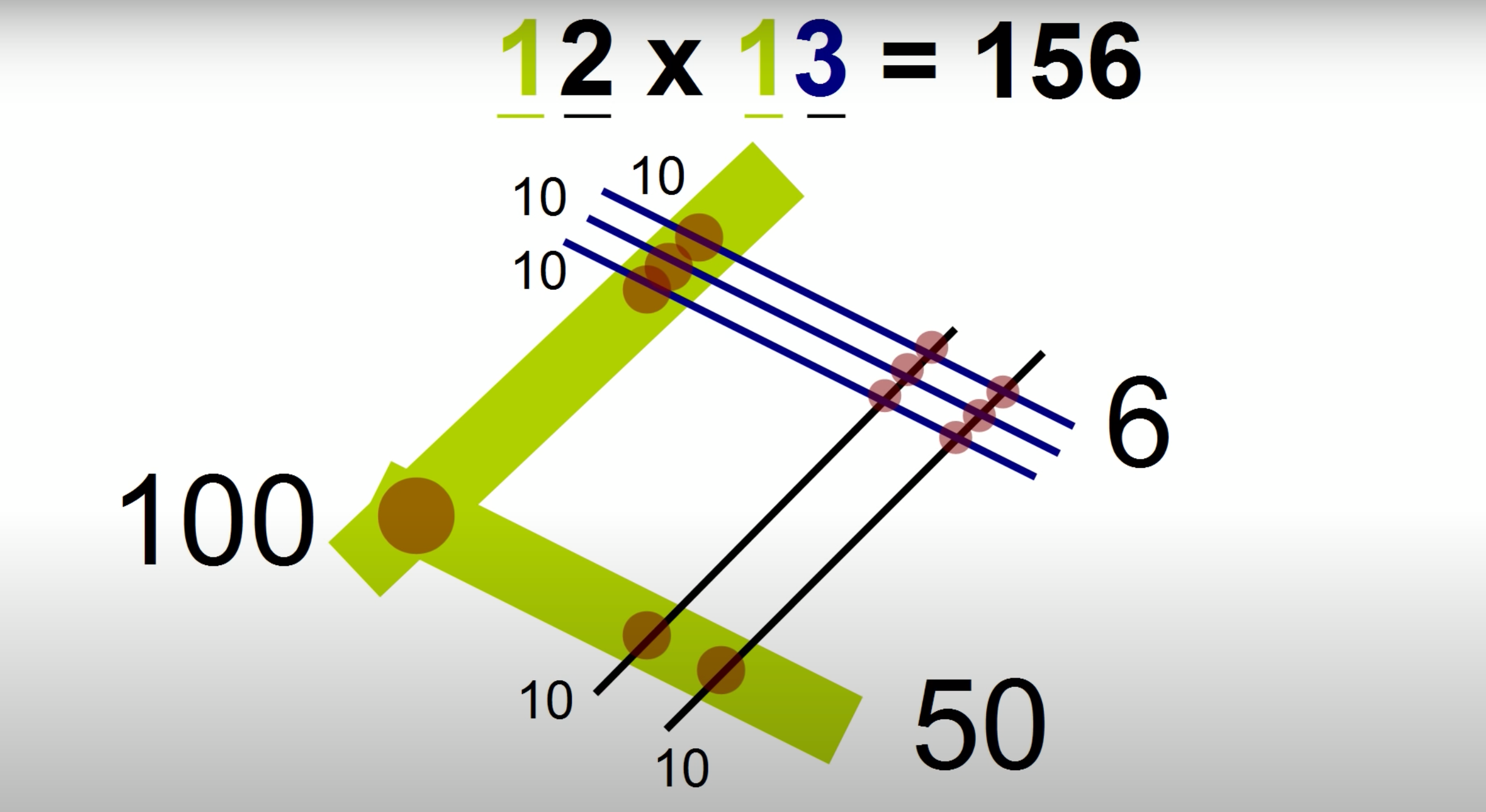
После того как вы нанесете на лист все линии, вам останется лишь нарисовать точки в местах пересечения и их подсчитать. В правом углу квадрата получится 6 точек (пересечения двух черных и трех синих линий). Эта цифра будет означать «единицы» в полученном числе, то есть стоять на последнем месте.
В нижнем углу видим 2 точки (пересечения разряда «десятков» числа 13 и двух черных линий). В верхнем углу – 3 точки (пересечение разряда «десятков» числа 12 и трех синих линий). Теперь сложим их вместе. Полученный результат 5 будет представлять разряд «десятков» в итоговом числе.
Наконец, в левом углу получилась 1 точка. В итоговом числе цифра 1 будет представлять разряд «сотен».
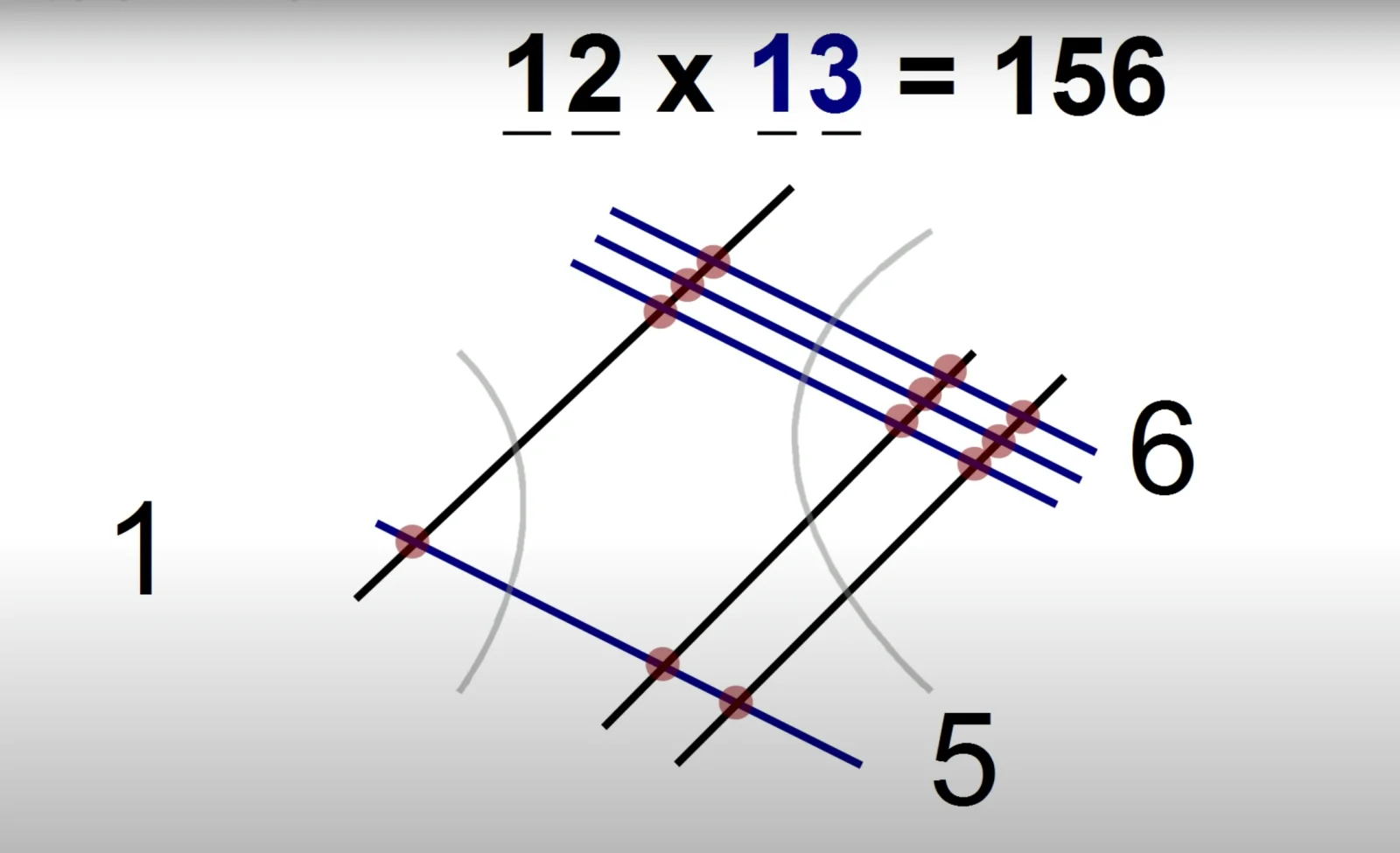
Возможно, вам будет удобнее отделять разряды на квадрате изогнутыми вертикальными линиями (как показано на рисунке). В любом случае, поставив каждую цифру на свое место, вы получите: 12 x 13 = 156 .
Этот метод работает и с гораздо большими числами. Просто попробуйте!
Вот видеопример как можно посчитать: 31х32, 213 x 13 и 103х23
Источник
Старинные способы умножения
Презентация к уроку
Загрузить презентацию (411 кБ)
“Счёт и вычисления – основа порядка в голове”.
Песталоцци
Цель:
- Познакомиться со старинными приемами умножения.
- Расширить знания по различным приемам умножения.
- Научиться выполнять действия с натуральными числами, используя старинные способы умножения .
Содержание.
- Старинный способ умножение на 9 на пальцах
- Умножение методом Ферроля.
- Японский способ умножения.
- Итальянский способ умножения (“Сеткой”)
- Русский способ умножения.
- Индийский способ умножения.
Ход занятия
Актуальность использования приемов быстрого счета.
В современной жизни каждому человеку часто приходится выполнять огромное количество расчётов и вычислений. Поэтому цель моей работы – показать лёгкие, быстрые и точные методы счёта, которые не только помогут вам во время каких-либо расчётах, но вызовут немалое удивление у знакомых и товарищей, ведь свободное выполнение счётных операций в значительной степени может свидетельствовать о незаурядности вашего интеллекта. Основополагающим элементом вычислительной культуры являются сознательные и прочные вычислительные навыки. Проблема формирования вычислительной культуры актуальна для всего школьного курса математики, начиная с начальных классов, и требует не простого овладения вычислительными навыками, а использования их в различных ситуациях. Владение вычислительными умениями и навыками имеет большое значение для усвоения изучаемого материала, позволяет воспитывать ценные трудовые качества: ответственное отношение к своей работе, умение обнаруживать и исправлять допущенные в работе ошибки, аккуратное исполнение задания, творческое отношение к труду. Однако, в последнее время уровень вычислительных навыков, преобразований выражений имеет ярко выраженную тенденцию к снижению, учащиеся допускают массу ошибок при подсчетах, все чаще используют калькулятор, не мыслят рационально, что отрицательно сказывается на качестве обучения и уровне математических знаний учащихся в целом. Одной из составляющих вычислительной культуры является устный счёт, который имеет большое значение. Умение быстро и правильно произвести несложные вычисления “в уме” необходимо для каждого человека.
Старинные способы умножения чисел.
1. Старинный способ умножение на 9 на пальцах
Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9 x 3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9 x 3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.
2. Умножение методом Ферроля.
Для умножения единиц произведения переумножения перемножают единицы множителей, для получения десятков, умножают десятки одного на единицы другого и наоборот и результаты складывают, для получения сотен перемножают десятки. Методом Ферроля легко перемножать устно двухзначные числа от 10 до 20.
б) 1х4+2х1=6, пишем 6
3. Японский способ умножения
Такой прием напоминает умножение столбиком, но проводится довольно долго.
Использование приема. Допустим, нам надо умножить 13 на 24. Начертим следующий рисунок:
Этот рисунок состоит из 10 линий (количество может быть любым)
- Эти линии обозначают число 24 (2 линии, отступ, 4 линии)
- А эти линии обозначают число 13 (1 линия, отступ, 3 линии)
Теперь нужно сосчитать пересечения линий на всех четырех концах следующим способом:
(пересечения на рисунке указаны точками)
Количество пересечений:
- Верхний левый край: 2
- Нижний левый край: 6
- Верхний правый: 4
- Нижний правый: 12
1) Пересечения в верхнем левом крае (2) – первое число ответа
2) Сумма пересечений нижнего левого и верхнего правого краев (6+4) – второе число ответа
3) Пересечения в нижнем правом крае (12) – третье число ответа.
Получается: 2; 10; 12.
Т.к. два последних числа – двузначные и мы не можем их записать, то записываем только единицы, а десятки прибавляем к предыдущему.
4. Итальянский способ умножения (“Сеткой”)
В Италии, а также во многих странах Востока, этот способ приобрел большую известность.
Например, умножим 6827 на 345.
1. Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте.
2. Умножаем число каждого ряда последовательно на числа каждой колонки.
т.е.
- 6*3 = 18. Записываем 1 и 8
- 8*3 = 24. Записываем 2 и 4
Если при умножении получается однозначное число, записываем вверху 0, а внизу это число.
(Как у нас в примере при умножении 2 на 3 получилось 6. Вверху мы записали 0, а внизу 6)
3. Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.
5. Русский способ умножения.
Этот прием умножения использовался русскими крестьянами примерно 2-4 века назад, а разработан был еще в глубокой древности. Суть этого способа та:“На сколько мы делим первый множитель, на столько умножаем второй”.Вот пример: Нам нужно 32 умножить на 13. Вот как бы решили этот пример 3-4 века назад наши предки:
- 32 * 13 (32 делим на 2, а 13 умножаем на 2)
- 16 * 26 (16 делим на 2, а 26 умножаем на 2)
- 8 * 52 (и т.д.)
- 4 * 104
- 2 * 208
- 1 * 416 =416
Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат. Нетрудно понять, на чем этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение
Однако как поступить, если при этом приходится делить пополам число нечетное? Народный способ легко выходит из этого затруднения. Надо, — гласит правило, — в случае нечётного числа откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением. Практически это делают так, что все строки с четными левыми числами зачеркивают; остаются только те, которые содержат налево нечетное число. Приведем пример (звездочки указывают, что данную строку надо зачеркнуть):
- 19*17
- 9*34
- 4 *68*
- 2 *136*
- 1 *272
Сложив незачеркнутые числа, получаем вполне правильный результат:
- 17 + 34 + 272 = 323.
6. Индийский способ умножения.
Такой способ умножения использовали в Древней Индии.
Для умножения, например, 793 на 92 напишем одно число как множимое и под ним другое как множитель. Чтобы легче ориентироваться, можно использовать сетку (А) как образец.
Теперь умножаем левую цифру множителя на каждую цифру множимого, то есть, 9х7, 9х9 и 9х3. Полученные произведения пишем в сетку (Б), имея в виду следующие правила:
- Правило 1. Единицы первого произведения следует писать в той же колонке, что и множитель, то есть в данном случае под 9.
- Правило 2. Последующее произведения надо писать таким образом, чтобы единицы помещались в колонке непосредственно справа от предыдущего произведения.
Повторим весь процесс с другими цифрами множителя, следуя тем же правилам (С).
Затем складываем цифры в колонках и получаем ответ: 72956.
Как можно видеть, мы получаем большой список произведений. Индийцы, имевшие большую практику, писали каждую цифру не в соответствующую колонку, а сверху, насколько это было возможно. Затем они складывали цифры в колонках и получали результат.
Заключение
Мы вступили в новое тысячелетие! Грандиозные открытия и достижения человечества. Мы много знаем, многое умеем. Кажется чем-то сверхъестественным, что с помощью чисел и формул можно рассчитать полёт космического корабля, “экономическую — ситуацию” в стране, погоду на “завтра”, описать звучание нот в мелодии. Нам известно высказывание древнегреческого математика, философа, жившего в 4 веке д. н.э.- Пифагора — “Всё есть число!”.
Согласно философскому воззрению этого учёного и его последователей, числа управляют не только мерой и весом, но также всеми явлениями, происходящими в природе, и являются сущностью гармонии, царствующей в мире, душой космоса.
Описывая старинные способы вычислений и современные приёмы быстрого счёта, я попытался показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись.
“Кто с детских лет занимается математикой, тот развивает внимание, тренирует мозг, свою волю, воспитывает настойчивость и упорство в достижении цели”. (А.Маркушевич)
Источник
Как умножают японцы
Наши дети и мы привыкли умножать числа традиционным способом, записывая числа-множители столбиком.
Однако, в Азии детей учат совершенно другому приему умножения.
Умножая «в столбик», ребенку приходится держать в голове большие объемы данных. Японское умножение полезно показать всем детям, особенно любят данный способ визуалы и кинестеты. Ведь они могут увидеть умножение!
В этом видео мы рассказываем, как умножать по-японски:
Данный метод позволяет ребенку визуализировать умножение и решать примеры в рамках таблицы умножения и за ее пределами.
Например нам нужно умножить 12 на 12.
Шаг 1 — Горизонтально рисуем линии первого числа. Для каждого числа рисуется свое количество линий. Десятки и единицы разделяются промежутками. Например, для числа 12 единица рисуется одной линией. Двойка – чуть ниже двумя параллельными линиями. Для числа 36, 3 рисуется тремя линиями, 6 шестью параллельными линиями ниже и т.д.
Шаг 2 По аналогии с шагом 1, вертикальными линиями рисуем второе число 12:
Единицу – одной линией
Двойку – чуть отступив вправо двумя линиями
Шаг 3 Ставим на пересечениях линий точки
Шаг 4 Подсчитываем количество точек в трех группах, разделив их на «Рыбу»: хвост, голову и тело
Левый верхний угол – 1 (сотни)
Правый верхний и левый нижний углы (Диагональ) – 4 (десятки)
Правый нижний угол – 4 (единицы)
Шаг 5 Записываем результат: 144. Если у единиц или десятков получилось двухзначное число, то первая цифра добавляется к следующему разряду.
С помощью умножения «по-японски» дети могут легко посчитать любой пример таблицы умножения. Что нельзя сделать при традиционном подходе.
Забыв, ребенок легко может умножить 6 на 4 или 7 на 8.
Ему надо лишь нарисовать умножение!
Используйте этот прием и метод. И если ребенок на контрольной от волнения забудет таблицу умножения, он сможет на черновике посчитать «по-японски»!
В прошлое воскресенье, на занятиях в Школе спецагентов, детям очень понравился данный метод. Порисовав умножение, ребята применили еще два приема, которые позволили выучить таблицу умножения раз и навсегда.
В мире есть огромное количество уникальных техник, упрощающих жизнь и помогающих полюбить учиться.
Мы собрали их все, совместили со знанием детской психологией, добавили индвидуальный подход и обучаем детей лучшим мировым техникам обучения.
Давайте сделаем Вашим детям новогодний подарок — научим их учиться С удовольствием. Потому что учиться может быть очень увлекательно
Можно радоваться тому:
- Как здорово ты справился со всеми сложными словами и пишешь грамотно
- Как легко поддаются задачи по математике
- Как с помощью техники «Гамбургер» увлекательно пересказывать тексты
- Можно радоваться выученной таблице умножения, падежам, правилам русского и математике
- Можно побеждать сложных боссов, таких как физика или история
- И все это, спецагентскими приемами, необычными и увлекательнымиВ пакете стандрат дети научатся легко справляешься с самыми сложными заданиями по окружающему миру, математике, по русскому языку и красиво отвечать у доски.
- В пакете ПРО ребята изучат как эффективно учить и понимать английский, физику, историю, информатику.
- Научатся писать сочинения и изложения.
Мы используем собственную авторскую методику обучения.
Наши ученики не зубрят правила, они учатся думать, быть внимательными, верить в себя и не бояться трудностей, пишут грамотно и быстро и правильно считают.
Вам понравилась статья? Сохраните себе на стену, чтобы не потерять
Источник