Японский способ умножения презентация

3.Японский способ умножения Допустим, нам надо умножить 24 на 13

3.Японский способ умножения Допустим, нам надо умножить 24 на 13. Начертим следующий рисунок: 24 13 Верхний левый край: 2 Нижний левый край: 6 Верхний правый: 4 Нижний правый: 12. Х.

Слайд 11 из презентации «Cтаринные способы умножения»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Cтаринные способы умножения.pptx» можно в zip-архиве размером 364 КБ.

Похожие презентации

«Японская война» — Война c японией. Сокрушительный удар по Квантунской группировке войск на Дальнем Востоке явился одним из определяющих факторов разгрома Японии. В настоящее время территориальные проблемы препятствуют заключению мирного договора между Японией и Россией как преемницей СССР. (9 августа — 2 сентября ) 1945 год.

«Способы умножения» — Деление. Десятки располагаются в нижнем треугольнике, а единицы в верхнем. В Средние века совсем немногие владели искусством умножения. Перемножим способом «Ревность» числа 1998 и 987. Русский крестьянский способ. Умножение. Умножение методом «Ревность». Затем складываются оставшиеся числа в правом столбце – получается 1972026.

«Японская архитектура» — Природа «прорастает» архитектурой, и архитектура затем, в свою очередь, «прорастает» природой. Конструкции в Японии, стране деревянной архитектуры, редко бывают тяжелыми и массивными. Исследуем характерные особенности японской архитектуры. Приобщаясь к природе, можно найти путь к истине, просветлению.

«Японский сад» — Сад компонуется небольшими растениями с присутствием хвойных пород, цветы в японских садах встречаются редко. Для европейца название “японский сад” условно и говорит о саде лаконичном, предназначенном для созерцания, а не развлечений. В японском саду обычно отсутствуют доминанты в виде остроконечных конусов, устремленных в небо.

«Японская культура» — Основой японской кухни является рис. Чайная церемония (яп. тя-но ю). Среди остальных жанров мультипликации выделяется большей ориентацией на взрослую аудиторию. Одежда. Национальная кухня. Оригами (яп.«сложенная бумага»). Икебана («кадо» — путь цветов). Японский язык всегда был важной составляющей японской культуры.

«Японская чайная церемония» — На восходе солнца. Начинается беседа. Ночная церемония. Вечерняя. Традиционные виды церемонии. Утренняя. Чайный домик должен быть простым и скромным. Весь процесс проходит в полном молчании. Японская чайная церемония. Чайный домик (тясицу). Порядок и символика. История. Чайный сад (тянива). Название «родзи» означает «земля, покрытая росой».

Источник

Проект по математике » Китайский и японский способы умножения»

ознакомиться со способами умножения натуральных чисел, которые не используются на уроках, и научиться их применять при вычислениях.

Скачать:

Вложение	Размер
proekt_po_matematike.ppt	618.5 КБ

Предварительный просмотр:

Подписи к слайдам:

Китайский и японский способы умножения натуральных чисел

Цель: ознакомиться со способами умножения натуральных чисел, которые не используются на уроках, и научиться их применять при вычислениях.

Актуальность: У многих ребят возникают проблемы в учёбе. Из беседы с ребятами 4, 5, 6, 7 классов и учителями я узнал, что это связано с тем, что они плохо считают. У некоторых сложности с таблицей умножения! Я решил выяснить : «Надо ли знать таблицу умножения?»

В школе изучают таблицу умножения, а затем умножают числа в столбик. Я выяснил, что это не единственный способ умножения. На самом деле, существует несколько десятков способов умножения многозначных чисел.

Русско-крестьянский способ , Квадрат Пифагора, Таблица Оконешникова, Индийский способ умножения, Египетский способ умножения, Китайский способ умножения, Японский способ умножения и др .

В данной работе остановлюсь на китайском и японском способах умножения . Мне они показались наиболее простыми.

Китайский способ умножения. При умножении чисел считаются точки пересечения прямых, которые соответствуют количеству цифр каждого разряда обоих множителей.

Пример : умножим 21 на 1 3. В первом множителе 2 десятка и 1единица, значит строим 2 параллельные прямые и поодаль 1 прямую.

Во втором множителе 1 десяток и 3 единицы. Строим параллельно 1 и поодаль 3 прямые, пересекающие прямые первого множителя. Прямые пересеклись в точках, количество которых и есть ответ, то есть 21 х 13 = 273

Японский способ умножения – это графический способ с использованием кругов и линий. Не менее интересный чем китайский. Даже чем-то на него похож.

Пример: умножим 12 на 34. Так как второй множитель двузначное число, а первая цифра первого множителя 1 , строим два одиночных круга в верхней строке и два двоичных круга в нижней строке, так как вторая цифра первого множителя равна 2 .

Так как первая цифра второго множителя 3 , а вторая 4 , делим круги первого столбца на три части, второго столбца на четыре. Количество частей, на которые разделились круги и является ответом, то есть 12 х 34 = 408.

Заключение Работая над этой темой я узнал, что существует много различных, забавных и интересных способов умножения. Некоторыми в различных странах пользуются до сих пор. Но не все способы удобны в использовании, особенно при умножении многозначных чисел. В общем, таблицу умножения все-таки знать нужно!

Литература И.Я. Депман, Н.Я. Виленкин “За страницами учебника математики”. Л.Ф. Магницкий «Арифметика». Журнал «Математика» №15 2011г. Интернет-ресурсы.

Источник

Умножение японским методом

Умножение японским методом.

Слайд 14 из презентации «Необычные способы умножения»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Необычные способы умножения.ppt» можно в zip-архиве размером 1929 КБ.

Умножение

«Умножение целых чисел» — Остается одна возможность (-5)*(-3)=15. Какие числа называются положительными ? Правила знаков при умножении ( + ) · ( + ) = ( + ) ( — ) · ( — ) = ( + ) ( + ) · ( — ) = ( — ) ( — ) · ( + ) = ( -). Создание проблемной ситуации. Самостоятельная работа (работа в парах). Тема урока: Умножение целых чисел.

«Письменное умножение» — Класс делится на 3 команды. 1) Вычисли глубину самого глубокого в Эстонии озера — Рыуге Суурярв. 3. Игра. Тогда Осёл и Козёл поменялись местами. 2) Восстановите цепочку вычислений. По дороге повстречал Елену Прекрасную. Далее >>. Кто был проводник — правдолюб или лгун ? Натуральные числа умножаются поразрядно, начиная с разряда единиц.

«Знакомство с умножением» — Организационный момент. Задание усложняется. Вычислительный тренинг. Исследуем. Найти произведение. Умножаем и делим. Презентация урока математики, 2 класс. Трудные случаи умножения. Рассуждаем и доказываем. Разминка. Больше, меньше, равно. Рассуждаем. Составляем и решаем задачу. Посчитать количество клеток в каждой лесенке.

«Способы умножения» — Умножение. Перемножим способом «Ревность» числа 1998 и 987. Результаты записываются справа и снизу от таблицы – получается 1972026. Деление. Затем складываются оставшиеся числа в правом столбце – получается 1972026. В Средние века совсем немногие владели искусством умножения. Десятки располагаются в нижнем треугольнике, а единицы в верхнем.

«Умножение круглых чисел» — Физминутка пешехода. Умножение круглых чисел. О чем мы будем говорить на уроке. Контрольные вопросы урока. Место остановки автобуса и троллейбуса. Опорная схема умножения круглых чисел «в строчку». В Ульяновске около 1900 пешеходных переходов. У вас получилось 1 000 000. Решение. Найди значения выражений, расположи их в порядке убывания.

«Письменное умножение на двузначное число» — План решения задачи. Умножение на двузначное число. Письменный прием умножения. Запомни алгоритм. Первый множитель. Первое неполное произведение. Письменное умножение на двузначное число. Выполнение задания. Мантейн. Восстанови стертые цифры.

Источник

Старинные способы умножения

Презентация к уроку

Загрузить презентацию (411 кБ)

“Счёт и вычисления – основа порядка в голове”.
Песталоцци

Цель:

• Познакомиться со старинными приемами умножения.
• Расширить знания по различным приемам умножения.
• Научиться выполнять действия с натуральными числами, используя старинные способы умножения .

Содержание.

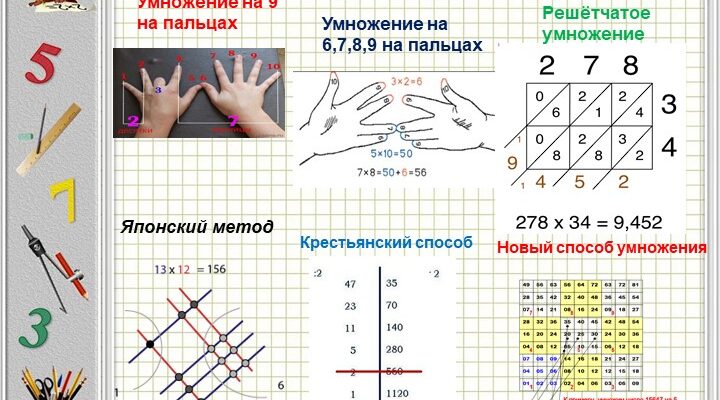
1. Старинный способ умножение на 9 на пальцах
2. Умножение методом Ферроля.
3. Японский способ умножения.
4. Итальянский способ умножения (“Сеткой”)
5. Русский способ умножения.
6. Индийский способ умножения.

Ход занятия

Актуальность использования приемов быстрого счета.

В современной жизни каждому человеку часто приходится выполнять огромное количество расчётов и вычислений. Поэтому цель моей работы – показать лёгкие, быстрые и точные методы счёта, которые не только помогут вам во время каких-либо расчётах, но вызовут немалое удивление у знакомых и товарищей, ведь свободное выполнение счётных операций в значительной степени может свидетельствовать о незаурядности вашего интеллекта. Основополагающим элементом вычислительной культуры являются сознательные и прочные вычислительные навыки. Проблема формирования вычислительной культуры актуальна для всего школьного курса математики, начиная с начальных классов, и требует не простого овладения вычислительными навыками, а использования их в различных ситуациях. Владение вычислительными умениями и навыками имеет большое значение для усвоения изучаемого материала, позволяет воспитывать ценные трудовые качества: ответственное отношение к своей работе, умение обнаруживать и исправлять допущенные в работе ошибки, аккуратное исполнение задания, творческое отношение к труду. Однако, в последнее время уровень вычислительных навыков, преобразований выражений имеет ярко выраженную тенденцию к снижению, учащиеся допускают массу ошибок при подсчетах, все чаще используют калькулятор, не мыслят рационально, что отрицательно сказывается на качестве обучения и уровне математических знаний учащихся в целом. Одной из составляющих вычислительной культуры является устный счёт, который имеет большое значение. Умение быстро и правильно произвести несложные вычисления “в уме” необходимо для каждого человека.

Старинные способы умножения чисел.

1. Старинный способ умножение на 9 на пальцах

Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9 x 3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9 x 3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.

2. Умножение методом Ферроля.

Для умножения единиц произведения переумножения перемножают единицы множителей, для получения десятков, умножают десятки одного на единицы другого и наоборот и результаты складывают, для получения сотен перемножают десятки. Методом Ферроля легко перемножать устно двухзначные числа от 10 до 20.

б) 1х4+2х1=6, пишем 6

3. Японский способ умножения

Такой прием напоминает умножение столбиком, но проводится довольно долго.

Использование приема. Допустим, нам надо умножить 13 на 24. Начертим следующий рисунок:

Этот рисунок состоит из 10 линий (количество может быть любым)

• Эти линии обозначают число 24 (2 линии, отступ, 4 линии)
• А эти линии обозначают число 13 (1 линия, отступ, 3 линии)

Теперь нужно сосчитать пересечения линий на всех четырех концах следующим способом:

(пересечения на рисунке указаны точками)

Количество пересечений:

• Верхний левый край: 2
• Нижний левый край: 6
• Верхний правый: 4
• Нижний правый: 12

1) Пересечения в верхнем левом крае (2) – первое число ответа

2) Сумма пересечений нижнего левого и верхнего правого краев (6+4) – второе число ответа

3) Пересечения в нижнем правом крае (12) – третье число ответа.

Получается: 2; 10; 12.

Т.к. два последних числа – двузначные и мы не можем их записать, то записываем только единицы, а десятки прибавляем к предыдущему.

4. Итальянский способ умножения (“Сеткой”)

В Италии, а также во многих странах Востока, этот способ приобрел большую известность.

Например, умножим 6827 на 345.

1. Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте.

2. Умножаем число каждого ряда последовательно на числа каждой колонки.

т.е.

• 6*3 = 18. Записываем 1 и 8
• 8*3 = 24. Записываем 2 и 4

Если при умножении получается однозначное число, записываем вверху 0, а внизу это число.

(Как у нас в примере при умножении 2 на 3 получилось 6. Вверху мы записали 0, а внизу 6)

3. Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.

5. Русский способ умножения.

Этот прием умножения использовался русскими крестьянами примерно 2-4 века назад, а разработан был еще в глубокой древности. Суть этого способа та:“На сколько мы делим первый множитель, на столько умножаем второй”.Вот пример: Нам нужно 32 умножить на 13. Вот как бы решили этот пример 3-4 века назад наши предки:

• 32 * 13 (32 делим на 2, а 13 умножаем на 2)
• 16 * 26 (16 делим на 2, а 26 умножаем на 2)
• 8 * 52 (и т.д.)
• 4 * 104
• 2 * 208
• 1 * 416 =416

Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат. Нетрудно понять, на чем этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение

Однако как поступить, если при этом приходится делить пополам число нечетное? Народный способ легко выходит из этого затруднения. Надо, — гласит правило, — в случае нечётного числа откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением. Практически это делают так, что все строки с четными левыми числами зачеркивают; остаются только те, которые содержат налево нечетное число. Приведем пример (звездочки указывают, что данную строку надо зачеркнуть):

• 19*17
• 9*34
• 4 *68*
• 2 *136*
• 1 *272

Сложив незачеркнутые числа, получаем вполне правильный результат:

• 17 + 34 + 272 = 323.

6. Индийский способ умножения.

Такой способ умножения использовали в Древней Индии.

Для умножения, например, 793 на 92 напишем одно число как множимое и под ним другое как множитель. Чтобы легче ориентироваться, можно использовать сетку (А) как образец.

Теперь умножаем левую цифру множителя на каждую цифру множимого, то есть, 9х7, 9х9 и 9х3. Полученные произведения пишем в сетку (Б), имея в виду следующие правила:

• Правило 1. Единицы первого произведения следует писать в той же колонке, что и множитель, то есть в данном случае под 9.
• Правило 2. Последующее произведения надо писать таким образом, чтобы единицы помещались в колонке непосредственно справа от предыдущего произведения.

Повторим весь процесс с другими цифрами множителя, следуя тем же правилам (С).

Затем складываем цифры в колонках и получаем ответ: 72956.

Как можно видеть, мы получаем большой список произведений. Индийцы, имевшие большую практику, писали каждую цифру не в соответствующую колонку, а сверху, насколько это было возможно. Затем они складывали цифры в колонках и получали результат.

Заключение

Мы вступили в новое тысячелетие! Грандиозные открытия и достижения человечества. Мы много знаем, многое умеем. Кажется чем-то сверхъестественным, что с помощью чисел и формул можно рассчитать полёт космического корабля, “экономическую — ситуацию” в стране, погоду на “завтра”, описать звучание нот в мелодии. Нам известно высказывание древнегреческого математика, философа, жившего в 4 веке д. н.э.- Пифагора — “Всё есть число!”.

Согласно философскому воззрению этого учёного и его последователей, числа управляют не только мерой и весом, но также всеми явлениями, происходящими в природе, и являются сущностью гармонии, царствующей в мире, душой космоса.

Описывая старинные способы вычислений и современные приёмы быстрого счёта, я попытался показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись.

“Кто с детских лет занимается математикой, тот развивает внимание, тренирует мозг, свою волю, воспитывает настойчивость и упорство в достижении цели”. (А.Маркушевич)

Источник