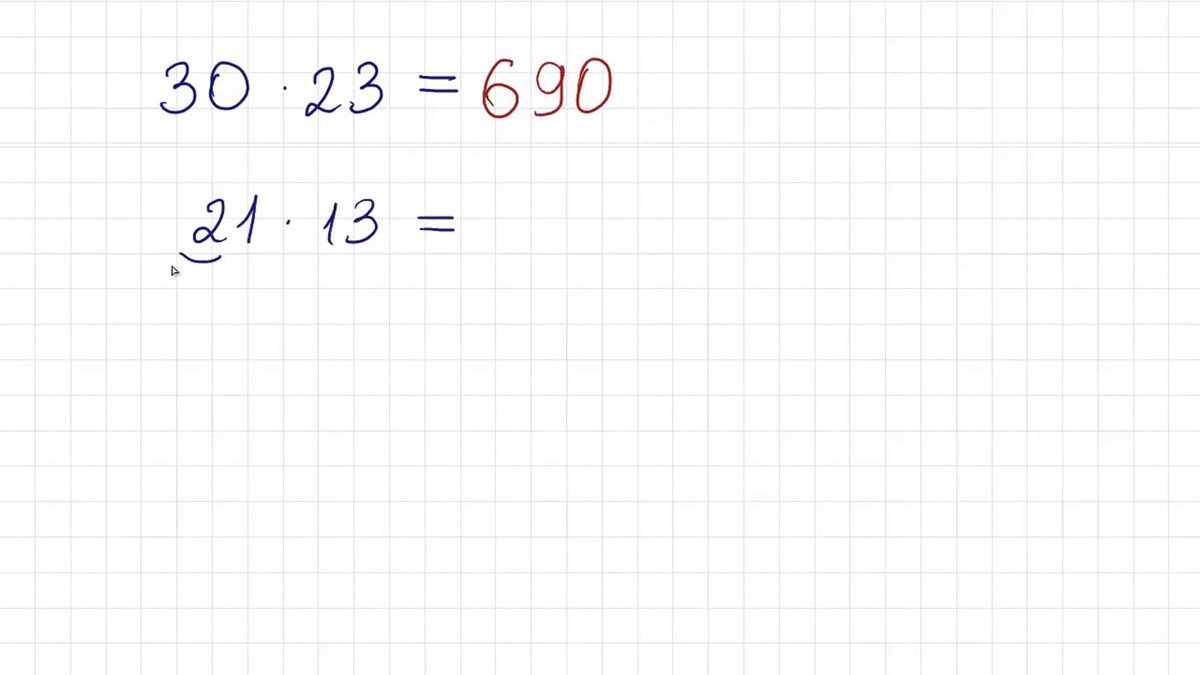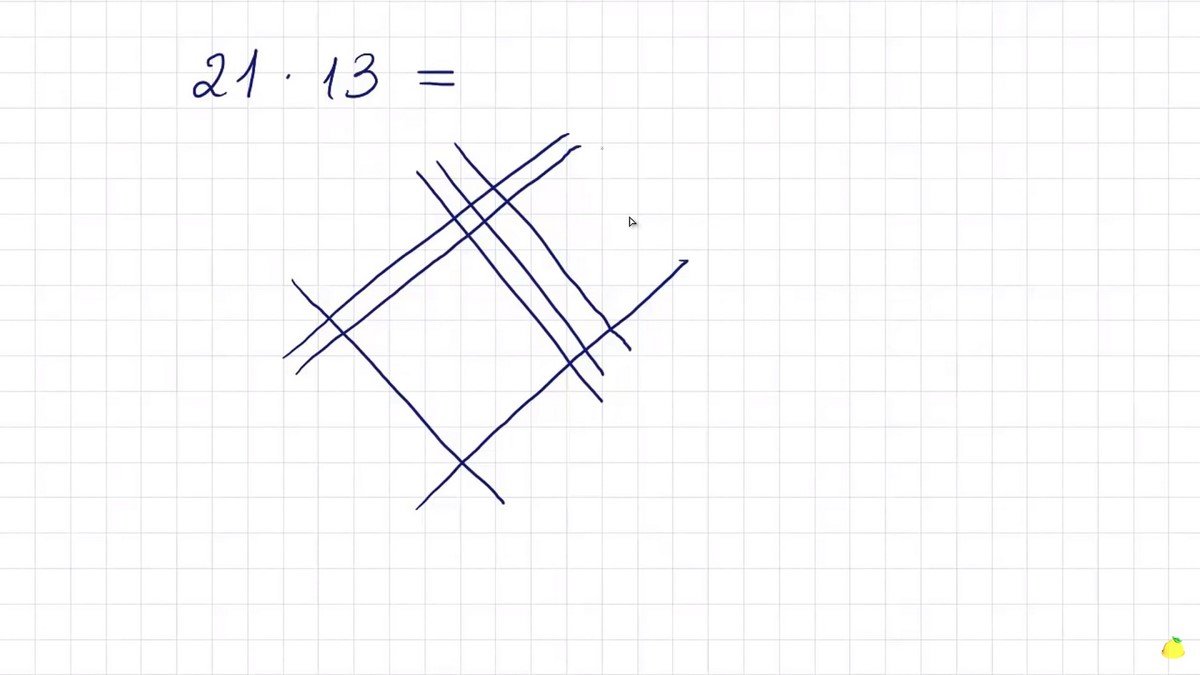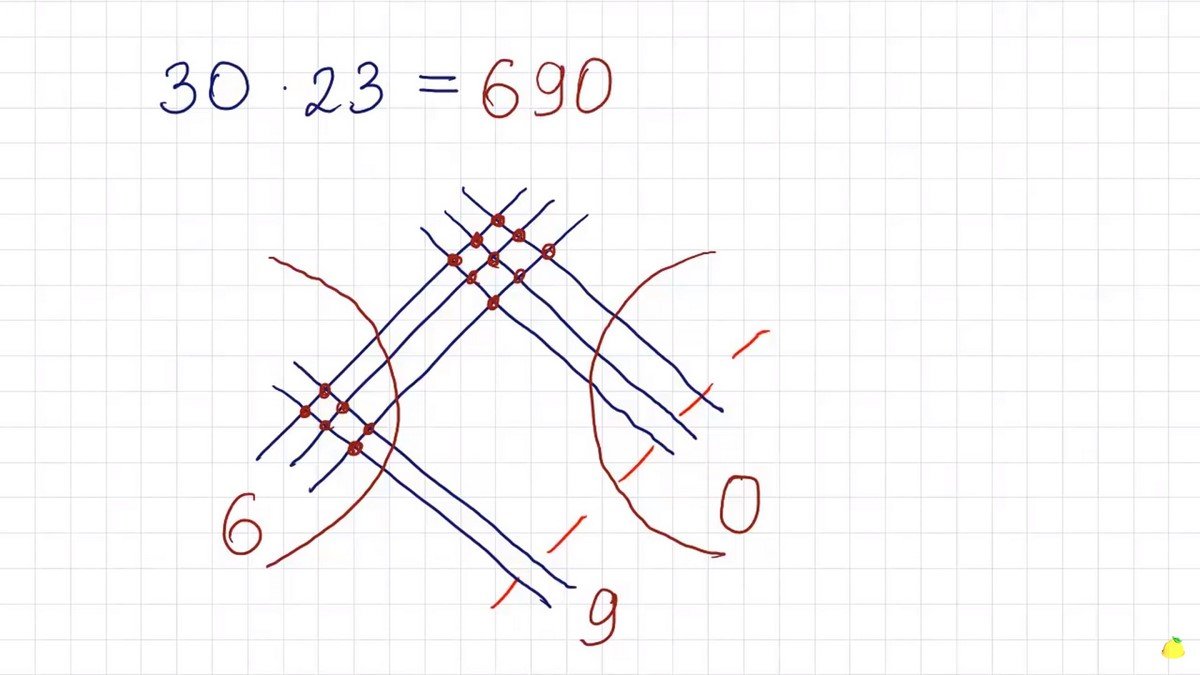Как умножают числа в Японии — спойлер: очень красиво. Забудьте о столбиках, всё намного проще, чем кажется
Девушка, преподающая математику в одной из лондонских школ, решила показать подписчикам японский метод умножения двузначных чисел и произвела фурор. Оказывается, можно обойтись без столбиков, а заодно почувствовать себя Сальвадором Дали. Правда, не всех впечатлил фокус, ведь 2020 год диктует новые правила.
Учительница математики из Лондона с ником jesslouisec ведёт аккаунт в TikTok, где доказывает, что её предмет может быть не только сложным и скучным (привет, математичка), но ещё и довольно интересным.

В своих роликах jesslouisec знакомит 134 тысячи подписчиков с нюансами, о которых обычно не рассказывают в школе. Например, она может помочь сдать ЕГЭ, рассказав, как легко умножить любую цифру на двузначное число — без регистрации, СМС и калькулятора.
Кроме того, учительница показывает альтернативные и, на первый взгляд, очень странные способы умножения двузначных чисел в столбик.
А для тех, кого не впечатлили эти фокусы, девушка приготовила математическое фаталити, сняв ролик о японском способе умножения. Видео стало очередным доказательством мема о том, что всегда найдётся азиат, который сделает что-либо лучше тебя.
Чтобы умножить два двузначных числа по методу jesslouisec, необходимо нарисовать параллельно количество линий, соответствующих первому числу. Десятки и единицы отдельно одни над другими — это важно.

Затем то же самое нужно проделать со вторым числом, но линии должны идти перпендикулярно первым. Ниже — десятки, выше — единицы.

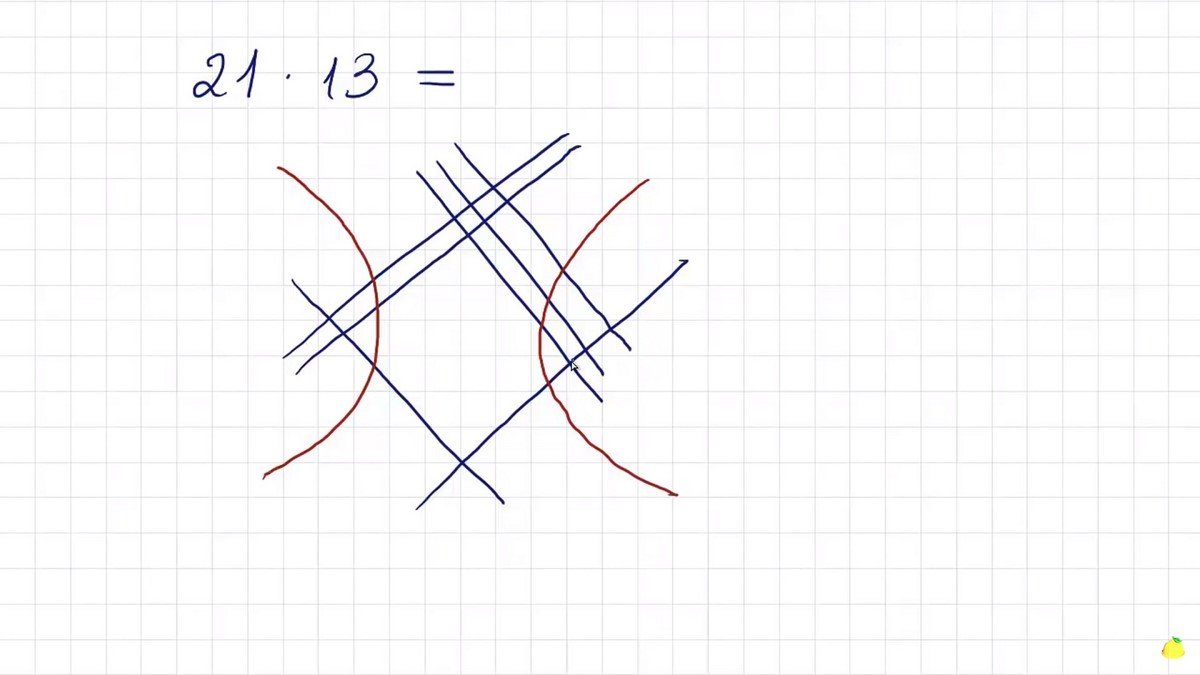
Дальше следует включить навыки художника и снабдить рисунок двумя грустными смайлами. Область по левую сторону от первой изогнутой линии будет сотнями вашего ответа, по правую — единицами, а всё, что останется посередине, — десятками.
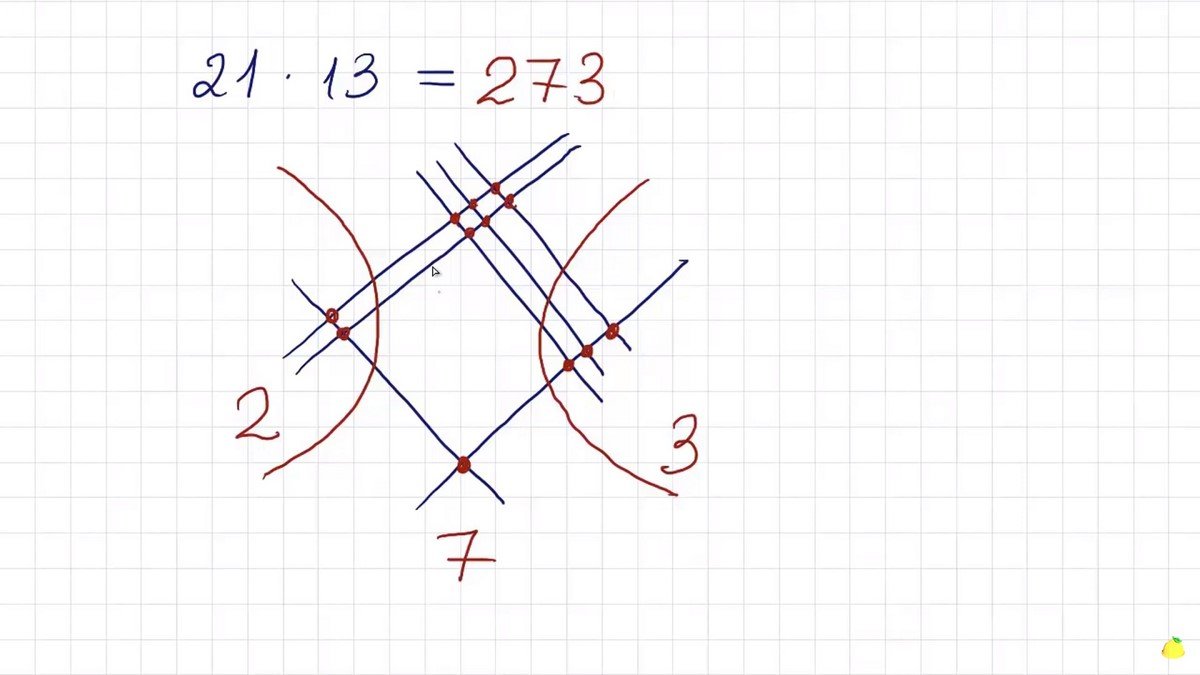
Изогнутые линии должны зеркально повторять друг друга. На следующем этапе останется лишь пересчитать количество точек пересечения перпендикулярных линий. В части сотен таких точек восемь, в части десятков — тоже восемь, единиц оказалось две.
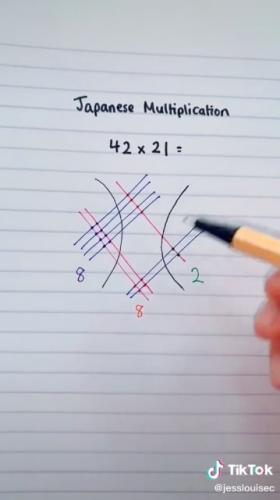
Метод jesslouisec настолько прост и красив, что не требует дополнительных объяснений — освоить технику можно за несколько секунд. Это, конечно, не научное открытие, которое сделал заключённый в тюрьме Вашингтона, но тоже неплохо.
Для скептиков, кто решил, что jesslouisec сама выдумала этот способ, есть аргумент: этот трюк действительно известен как японский метод простого умножения многозначных чисел или способ индейцев Майя.
Считается, что систему придумали индейцы древней цивилизации, которые жили в районах Центральной Америки ещё в XVI веке до нашей эры, а японцы стали применять его для обучения подрастающего поколения.
Тем не менее про метод знали далеко не все. Таких людей ролик jesslouisec разозлил.
Это намного проще, чем то, чему нас учили в школе. В некотором смысле я в шоке.
ПОЧЕМУ НАМ НЕ ПОКАЗАЛИ ЭТО РАНЬШЕ.
Правда, далеко не всем понравился японский метод умножения. Некоторые решили, что в 2020 году он уже не актуален.
Кто будет тратить на это время.
Мой айфон сделает то же самое за две секунды.
Впрочем, не стоит недооценивать важность математики в современной жизни, ведь правильное использование полученных знаний может помочь любому школьнику стать королём ЕГЭ — для успеха потребуется лишь Бритни Спирс и немного смелости.
Администрация школы в Нью-Йорке решила не изобретать велосипед и придумала такой способ изучения математики, который понравится любому ребёнку: включайте компьютер, пора играть в MMORPG.
Источник
Обмен опытом
Суть китайско-японского метода
Суть китайского метода состоит в визуализации произведения с помощью графического изображения процесса умножения. Другими словами, числа изображаются в виде прямых линий, сотни, десятки и единицы отделяются промежутками и располагаются параллельно друг другу на плоскости. Один из множителей располагается горизонтально сверху вниз, второй — вертикально слева направо. Количество пересечения линий, образующих десятки при умножении двузначных чисел, будет первой цифрой в произведении. Точки пересечения десятков и единиц — вторая цифра результата, количество точек, образовавшихся при пересечении всех единиц — третья цифра.
Перемножим два двузначных числа: 13*12=156
Шаг 1 Горизонтально рисуем линии первого числа 13:
Единицу – одной линией. Тройку – чуть ниже тремя параллельными линиями
Шаг 2 Вертикальными линиями слева направо рисуем второе число 12:
Единицу – одной линией
Двойку – чуть отступив вправо двумя линиями
Шаг 3 Подсчитываем количество точек в трех группах:
Левый верхний угол – 1 (Сотни)
Правый верхний и левый нижний углы (Диагональ) – 5 (Десятки)
Правый нижний угол – 6 (Единицы)
Шаг 4 Подсчитываем результат:

Перемножим два двузначных числа: 15*23=345
Источник
Как в Японии учат детей умножению и стоит ли нам пользоваться этим методом
Японцы — известные мастера на всякие выдумки. Оказывается, в младших классах они учат детей довольно любопытному методу умножения. Нас всегда учили считать в столбик, но для этого нужно хорошо знать таблицу умножения. Японский же метод подойдет любому, потому его обычно используют младшеклассники и дошкольники.
Его можно назвать графическим методом. Для того, чтобы узнать произведение двузначных чисел, достаточно нарисовать несколько черточек. Сейчас мы всё объясним.
Итак, например, нам нужно умножить 21 на 13. Число 21 мы представляем в виде трех линий, две линии это двойка, и еще одна представляет единицу. Число 13 мы представляем также в виде линий, но уже перпендикулярных линиям предыдущего числа. Получаем своего рода сеть.
Далее отсекаем дугами правую и левую части рисунков. Левая часть соответствует сотням, а правая — единицам. Пространство между отсеченными участками — десяткам.
Следующий шаг — подсчитать в каждой части количество пересечений, их можно отметить точками. Собираем цифры слева направо в цельное число, которое и будет ответом. В нашем случае это 273.
Если в одном из множителей присутствует ноль, то на схеме его можно изобразить в качестве пунктирной линии. Пересечения линий с пунктиром не считаются за точку, которую нужно считать.
Также в подобном методе существует ряд нюансов, когда в секторах мы можем получить двузначные числа. Расписывать последовательность действий в таком случае довольно непросто, потому предлагаем тебе просто посмотреть видео.
Конечно, для расчетов этот метод мало подходит. Ведь рисовать придется довольно долго, калькулятор всё еще побеждает. Но для тренировки ума или просто для общего развития — отличный вариант.
Источник
Умножение: по-японски, по-итальянски и методом майя
Автор фото, Getty Images
Не заболела бы голова.
«Математика такая трудная. » Вы наверняка не раз слышали эту фразу, а, может быть, даже сами ее произносили вслух.
Для многих математические вычисления — дело непростое, но вот вам три несложных способа, которые помогут выполнить хотя бы одно арифметическое действие — умножение. Без калькулятора.
Вполне вероятно, что в школе вы познакомились с наиболее традиционным способом умножения: сначала вы выучили на память таблицу умножения, а уж затем стали в столбик перемножать каждую из цифр, которыми записываются многозначные числа.
Если вам надо перемножить многозначные числа, то, чтобы найти ответ, потребуется большой лист бумаги.
Но если от этого длинного набора идущих одна под другой строчек с цифрами у вас голова идет кругом, то есть и другие, более наглядные методы, которые могут вам помочь в этом деле.
Но тут пригодятся некоторые художественные навыки.
Давайте порисуем!
Как минимум три способа умножения связаны с рисованием пересекающихся линий.
1. Способ индейцев майя, или японский метод
Относительно происхождения этого способа существует несколько версий.
Трудно умножать в уме? Попробуйте метод майя и японцев
Мы быстро, просто и понятно объясняем, что случилось, почему это важно и что будет дальше.
Конец истории Подкаст
Некоторые говорят, что его придумали индейцы цивилизации майя, населявшие районы Центральной Америки до прибытия туда конкистадоров в XVI веке. Он также известен как японский метод умножения, поскольку учителя в Японии используют именно этот визуальный способ, когда учат младших школьников умножению.
Суть в том, что параллельные и перпендикулярные линии представляют цифры тех чисел, которые нужно перемножить.
Давайте умножим 23 на 41.
Для этого нам надо нарисовать две параллельные линии, представляющие 2, и, немного отступя, еще три линии, представляющие 3.
Затем, перпендикулярно к этим линиям мы нарисуем четыре параллельные линии, представляющие 4 и, чуть отступя, еще одну линию для 1.
Теперь нам надо пересчитать все точки пересечения этих линий. Именно так мы и получаем наш результат — 943, как если бы мы умножали в столбик.
Ну как, неужели трудно?
2. Индийский способ, или итальянское умножение «решеткой» — «джелозия»
Происхождение этого способа умножения тоже не ясно, однако он хорошо известен по всей Азии.
«Алгоритм «джелозия» передавался из Индии в Китай, затем в Аравию, а оттуда в Италию в XIV-XV веках, где он получил название «джелозия», поскольку внешне был похож на венецианские решетчатые ставни», — пишет Марио Роберто Каналес Виллануэва в своей книге, посвященной различным способам умножения.
Автор фото, Getty Images
Индийская или итальянская система умножения похожа на венецианские жалюзи
Давайте снова возьмем пример с умножением 23 на 41.
Теперь нам потребуется начертить таблицу из четырех клеток — по клетке на цифру. Подпишем сверху у каждой клетки соответствующую цифру — 2,3,4,1.
Затем надо разделить каждую клетку надвое по диагонали, чтобы получились треугольники.
Теперь мы сначала умножим первые цифры каждого числа, то есть 2 на 4, и запишем в первом треугольнике 0, а во втором 8.
Потом перемножим 3×4 и запишем 1 в первом треугольнике, а 2 во втором.
Проделаем то же самое и с другими двумя цифрами.
Когда все клетки нашей таблицы будут заполнены, мы складываем цифры в такой последовательности, как показано на видео, и записываем получившийся результат.
Трудно умножать в уме? Попробуйте индийский метод
Первая цифра у нас будет 0, вторая 9, третья 4, четвертая 3. Таким образом, результат получился: 943.
Как вам показалось, проще этот способ или нет?
Давайте попробуем еще один метод умножения с помощью рисунка.
Как и в предыдущем случае, для этого потребуется нарисовать таблицу.
Возьмем тот же пример: 23 x 41.
Тут нам надо разделить наши числа на десятки и единицы, поэтому 23 мы запишем как 20 в одной колонке, и 3 в другой.
По вертикали мы запишем наверху 40, а внизу 1 .
Затем мы перемножим числа по горизонтали и вертикали.
Трудно умножать в уме? Нарисуйте таблицу.
Но вместо того чтобы умножать 20 на 40, мы отбросим нули и просто перемножим 2 x 4, получив 8.
То же самое сделаем, умножая 3 на 40. Мы удерживаем в скобках 0 и умножаем 3 на 4 и получаем 12.
Проделаем то же самое с нижним рядом.
Теперь добавим нули: в левой верхней клетке у нас получилось 8, но мы отбросили два нуля — теперь мы их допишем и получится 800.
В правой верхней клетке, когда мы умножали 3 на 4(0), у нас получилось 12; теперь мы допишем ноль и получим 120.
Сделаем так же со всеми прочими удержанными нулями.
И наконец, мы складываем все четыре числа, полученных умножением в таблице.
Результат? 943. Ну как, помогло?
Важно разнообразие
Автор фото, Getty Images
Все способы хороши, главное — чтобы ответ сошелся
Что точно можно утверждать, — так это то, что все эти разные способы дали нам один и тот же результат!
Нам все-таки пришлось кое-что перемножить в процессе, но каждый шаг был проще, чем при умножении традиционным способом, и гораздо более наглядный.
Так почему же мало где в мире в обычных школах учат этим методам вычисления?
Одной из причин может быть упор на обучение «вычислениям в уме» — чтобы развивать умственные способности.
Однако Дэвид Уиз, учитель математики из Канады, работающий в государственных школах в Нью-Йорке, объясняет это иначе.
«Недавно я прочитал, что причина, по которой используется традиционный метод умножения, — это экономия бумаги и чернил. Этот метод не был придуман как самый простой для использования, но как самый экономный с точки зрения ресурсов, поскольку чернила и бумага были в дефиците», — объясняет Уиз.
Автор фото, Getty Images
Для некоторых методов вычисления только головы недостаточно, нужны еще и фломастеры
Невзирая на это, он полагает, что альтернативные методы умножения очень полезны.
«Я не думаю, что это полезно — сразу учить школьников умножению, заставляя их выучивать таблицу умножения, но не объясняя им при этом, откуда она взялась. Поскольку если они забудут одно число, то как они смогут продвинуться в решении задачи? Метод майя или японский метод необходим, потому что с его помощью вы можете понять общую структуру умножения, а это хорошее начало», — полагает Уиз.
Существует и ряд других способов умножения, например, русский или египетский, они не требуют дополнительных навыков рисования.
Как говорят специалисты, с которыми мы беседовали, все эти методы помогают лучше понять процесс умножения.
«Понятно, что все идет на пользу. Математика в сегодняшнем мире открыта как внутри, так и снаружи классной комнаты», — резюмирует Андреа Васкес, учительница математики из Аргентины.
Источник