Японский способ умножения чисел без калькулятора

Умножение по-японски, или как легко и быстро перемножить числа без калькулятора

Как умножают в японии: Учимся считать с помощью линий.

В век смартфонов-калькуляторов и голосовых помощников умножение больших чисел вручную уже кажется необычным и совершенно ненужным навыком. Но жизнь – непредсказуемая штука: никогда не знаешь, когда понадобится быстро что-то посчитать. И в этом деле идеальным помощником будет японский метод умножения (иногда его называют умножением по строкам). Все, что вам понадобится, – лист бумаги и ручка. Чтобы облегчить задачу, вы можете использовать чернила разных цветов, но это вовсе необязательно.

Давайте рассмотрим, как работает этот метод.

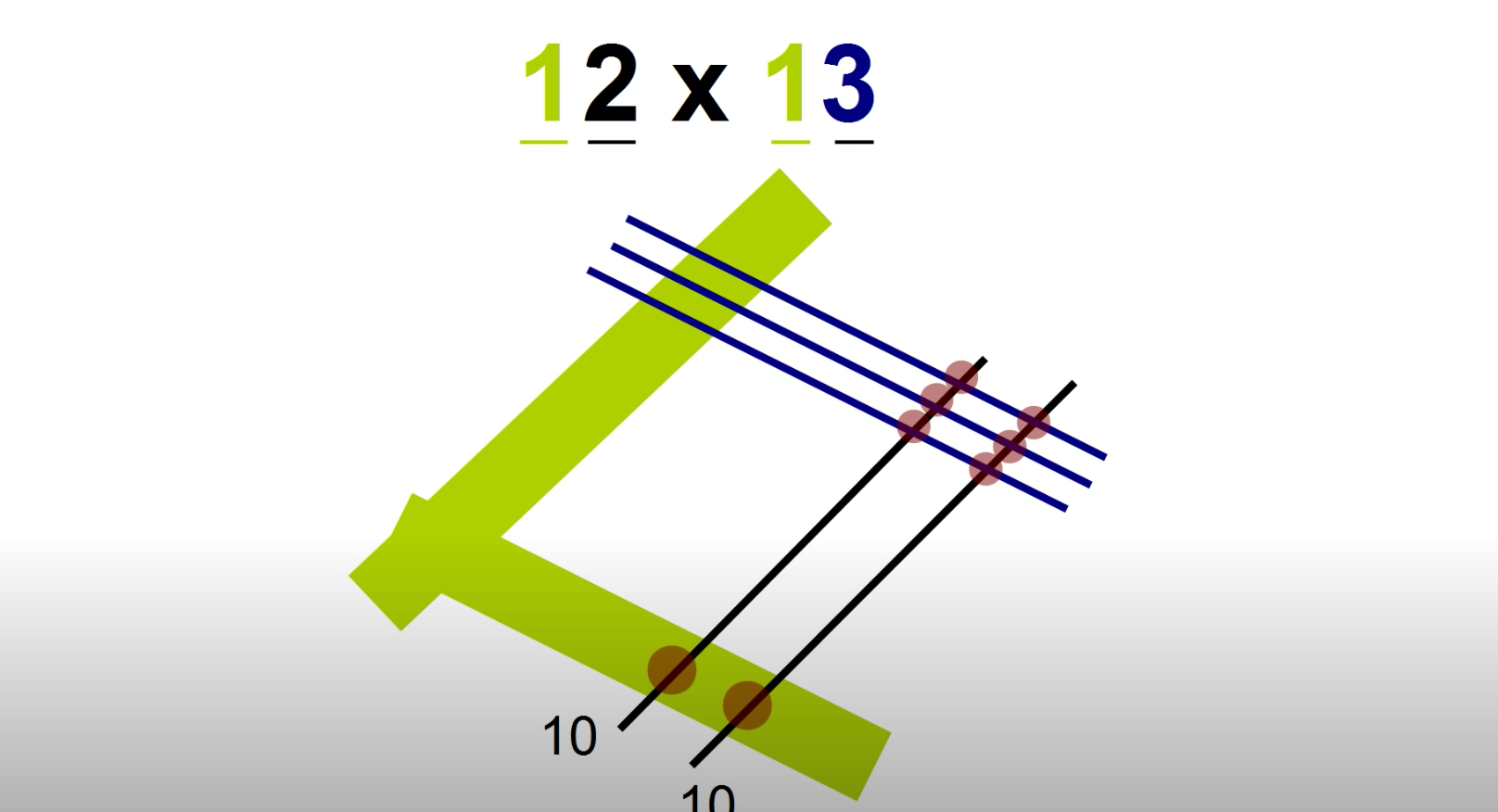
Посчитаем, сколько будет 12 x 13.

Первый шаг – рисуем линии. Один набор линий – для каждой «десятки» и параллельный набор – для разряда «единиц». У вас получится «квадрат», образованный одной линией для «десятков» числа 12 (зеленый цвет) + одной линией для «десятков» числа 13 (зеленый цвет) + двумя линиями для разряда «единиц» числа 12 (черный цвет) + тремя линиями для разряда «единиц» числа 13 (синий цвет). «Десятки» должны всегда располагаться слева, а прямоугольник – быть повернутым на 45 градусов.

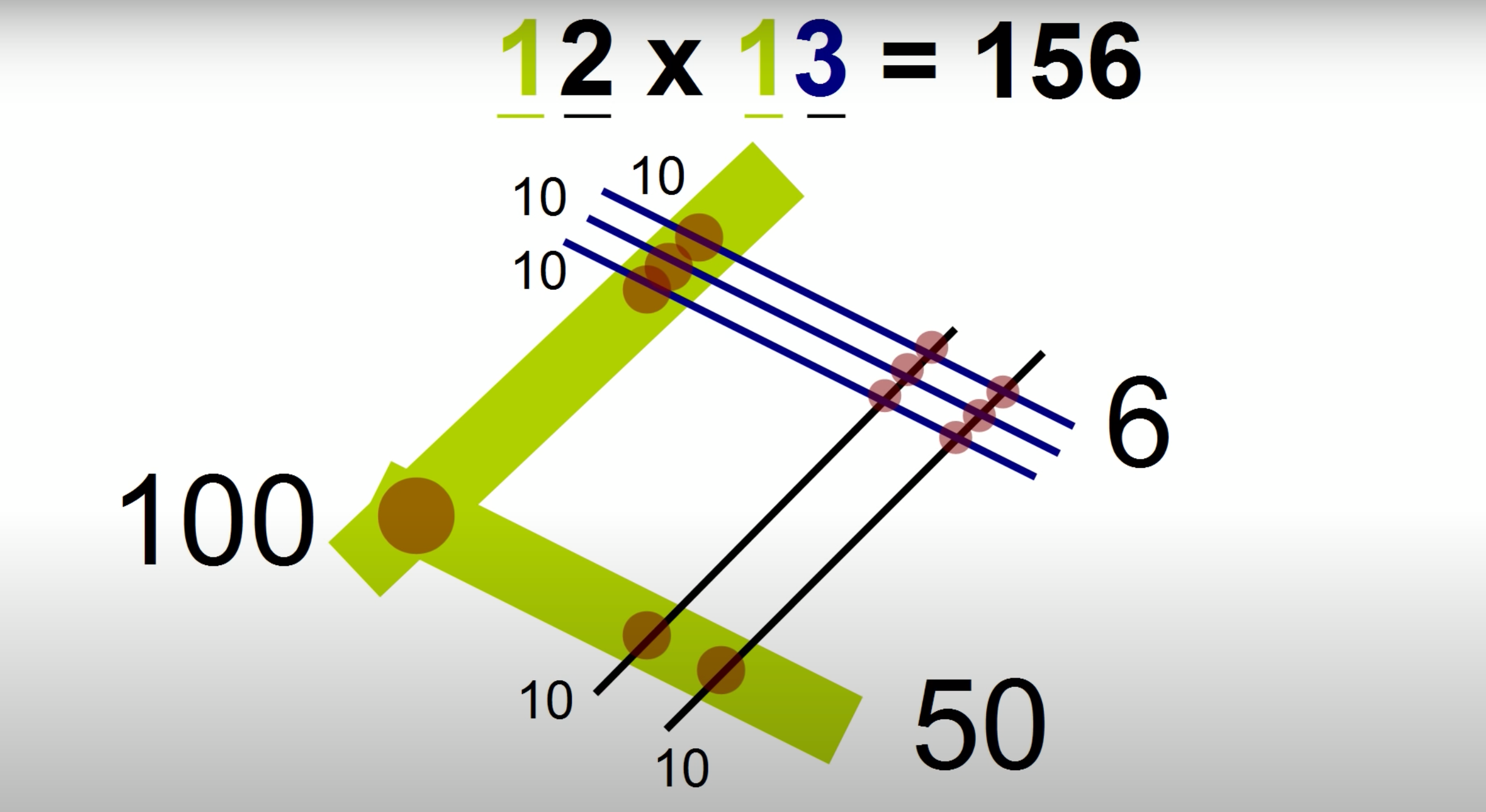
После того как вы нанесете на лист все линии, вам останется лишь нарисовать точки в местах пересечения и их подсчитать. В правом углу квадрата получится 6 точек (пересечения двух черных и трех синих линий). Эта цифра будет означать «единицы» в полученном числе, то есть стоять на последнем месте.

В нижнем углу видим 2 точки (пересечения разряда «десятков» числа 13 и двух черных линий). В верхнем углу – 3 точки (пересечение разряда «десятков» числа 12 и трех синих линий). Теперь сложим их вместе. Полученный результат 5 будет представлять разряд «десятков» в итоговом числе.

Наконец, в левом углу получилась 1 точка. В итоговом числе цифра 1 будет представлять разряд «сотен».

Возможно, вам будет удобнее отделять разряды на квадрате изогнутыми вертикальными линиями (как показано на рисунке). В любом случае, поставив каждую цифру на свое место, вы получите: 12 x 13 = 156 .

Этот метод работает и с гораздо большими числами. Просто попробуйте!

Вот видеопример как можно посчитать: 31х32, 213 x 13 и 103х23

Источник

Умножение: по-японски, по-итальянски и методом майя

Автор фото, Getty Images

Не заболела бы голова.

«Математика такая трудная. » Вы наверняка не раз слышали эту фразу, а, может быть, даже сами ее произносили вслух.

Для многих математические вычисления — дело непростое, но вот вам три несложных способа, которые помогут выполнить хотя бы одно арифметическое действие — умножение. Без калькулятора.

Вполне вероятно, что в школе вы познакомились с наиболее традиционным способом умножения: сначала вы выучили на память таблицу умножения, а уж затем стали в столбик перемножать каждую из цифр, которыми записываются многозначные числа.

Если вам надо перемножить многозначные числа, то, чтобы найти ответ, потребуется большой лист бумаги.

Но если от этого длинного набора идущих одна под другой строчек с цифрами у вас голова идет кругом, то есть и другие, более наглядные методы, которые могут вам помочь в этом деле.

Но тут пригодятся некоторые художественные навыки.

Давайте порисуем!

Как минимум три способа умножения связаны с рисованием пересекающихся линий.

1. Способ индейцев майя, или японский метод

Относительно происхождения этого способа существует несколько версий.

Трудно умножать в уме? Попробуйте метод майя и японцев

Мы быстро, просто и понятно объясняем, что случилось, почему это важно и что будет дальше.

Конец истории Подкаст

Некоторые говорят, что его придумали индейцы цивилизации майя, населявшие районы Центральной Америки до прибытия туда конкистадоров в XVI веке. Он также известен как японский метод умножения, поскольку учителя в Японии используют именно этот визуальный способ, когда учат младших школьников умножению.

Суть в том, что параллельные и перпендикулярные линии представляют цифры тех чисел, которые нужно перемножить.

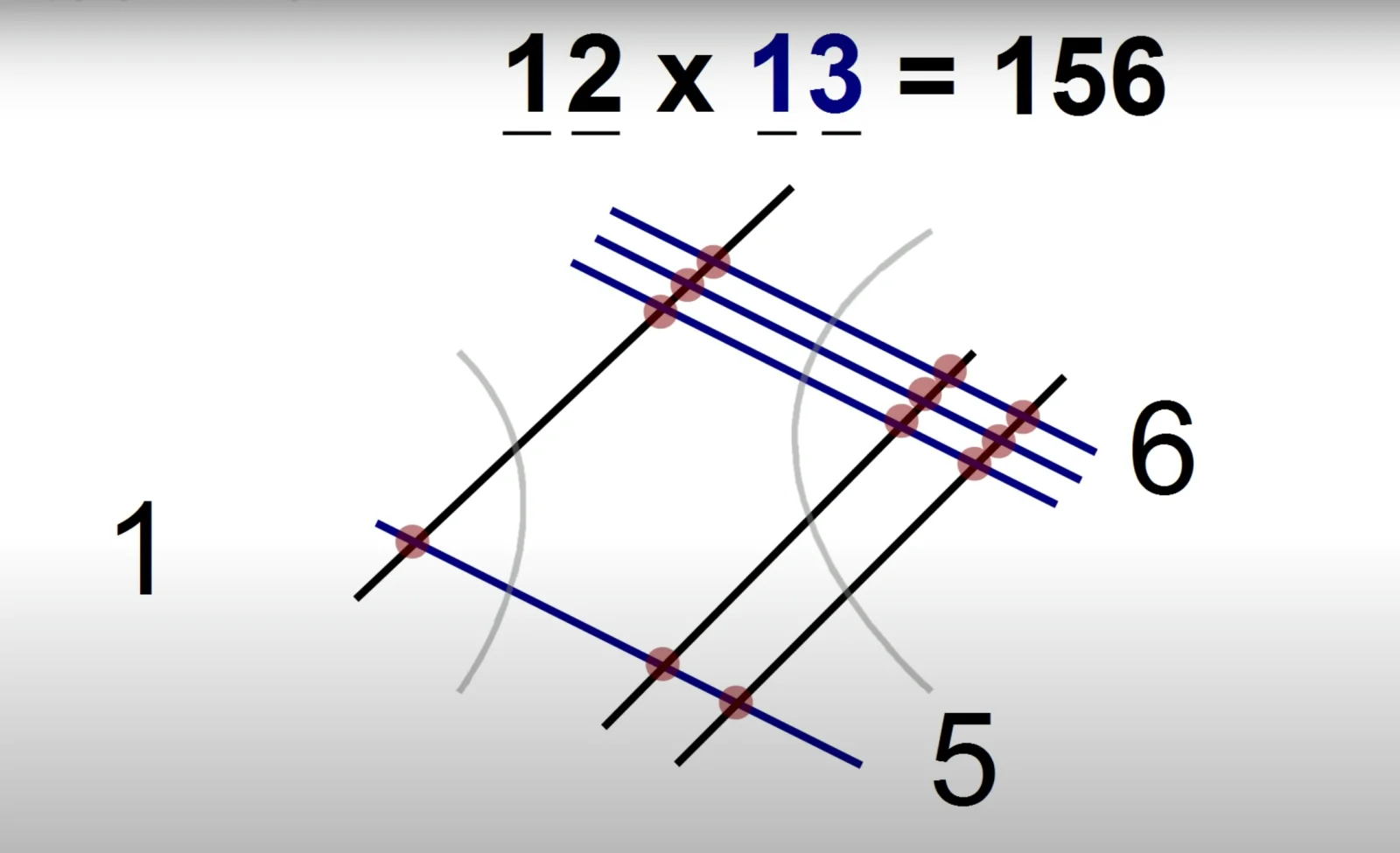
Давайте умножим 23 на 41.

Для этого нам надо нарисовать две параллельные линии, представляющие 2, и, немного отступя, еще три линии, представляющие 3.

Затем, перпендикулярно к этим линиям мы нарисуем четыре параллельные линии, представляющие 4 и, чуть отступя, еще одну линию для 1.

Теперь нам надо пересчитать все точки пересечения этих линий. Именно так мы и получаем наш результат — 943, как если бы мы умножали в столбик.

Ну как, неужели трудно?

2. Индийский способ, или итальянское умножение «решеткой» — «джелозия»

Происхождение этого способа умножения тоже не ясно, однако он хорошо известен по всей Азии.

«Алгоритм «джелозия» передавался из Индии в Китай, затем в Аравию, а оттуда в Италию в XIV-XV веках, где он получил название «джелозия», поскольку внешне был похож на венецианские решетчатые ставни», — пишет Марио Роберто Каналес Виллануэва в своей книге, посвященной различным способам умножения.

Автор фото, Getty Images

Индийская или итальянская система умножения похожа на венецианские жалюзи

Давайте снова возьмем пример с умножением 23 на 41.

Теперь нам потребуется начертить таблицу из четырех клеток — по клетке на цифру. Подпишем сверху у каждой клетки соответствующую цифру — 2,3,4,1.

Затем надо разделить каждую клетку надвое по диагонали, чтобы получились треугольники.

Теперь мы сначала умножим первые цифры каждого числа, то есть 2 на 4, и запишем в первом треугольнике 0, а во втором 8.

Потом перемножим 3×4 и запишем 1 в первом треугольнике, а 2 во втором.

Проделаем то же самое и с другими двумя цифрами.

Когда все клетки нашей таблицы будут заполнены, мы складываем цифры в такой последовательности, как показано на видео, и записываем получившийся результат.

Трудно умножать в уме? Попробуйте индийский метод

Первая цифра у нас будет 0, вторая 9, третья 4, четвертая 3. Таким образом, результат получился: 943.

Как вам показалось, проще этот способ или нет?

Давайте попробуем еще один метод умножения с помощью рисунка.

Как и в предыдущем случае, для этого потребуется нарисовать таблицу.

Возьмем тот же пример: 23 x 41.

Тут нам надо разделить наши числа на десятки и единицы, поэтому 23 мы запишем как 20 в одной колонке, и 3 в другой.

По вертикали мы запишем наверху 40, а внизу 1 .

Затем мы перемножим числа по горизонтали и вертикали.

Трудно умножать в уме? Нарисуйте таблицу.

Но вместо того чтобы умножать 20 на 40, мы отбросим нули и просто перемножим 2 x 4, получив 8.

То же самое сделаем, умножая 3 на 40. Мы удерживаем в скобках 0 и умножаем 3 на 4 и получаем 12.

Проделаем то же самое с нижним рядом.

Теперь добавим нули: в левой верхней клетке у нас получилось 8, но мы отбросили два нуля — теперь мы их допишем и получится 800.

В правой верхней клетке, когда мы умножали 3 на 4(0), у нас получилось 12; теперь мы допишем ноль и получим 120.

Сделаем так же со всеми прочими удержанными нулями.

И наконец, мы складываем все четыре числа, полученных умножением в таблице.

Результат? 943. Ну как, помогло?

Важно разнообразие

Автор фото, Getty Images

Все способы хороши, главное — чтобы ответ сошелся

Что точно можно утверждать, — так это то, что все эти разные способы дали нам один и тот же результат!

Нам все-таки пришлось кое-что перемножить в процессе, но каждый шаг был проще, чем при умножении традиционным способом, и гораздо более наглядный.

Так почему же мало где в мире в обычных школах учат этим методам вычисления?

Одной из причин может быть упор на обучение «вычислениям в уме» — чтобы развивать умственные способности.

Однако Дэвид Уиз, учитель математики из Канады, работающий в государственных школах в Нью-Йорке, объясняет это иначе.

«Недавно я прочитал, что причина, по которой используется традиционный метод умножения, — это экономия бумаги и чернил. Этот метод не был придуман как самый простой для использования, но как самый экономный с точки зрения ресурсов, поскольку чернила и бумага были в дефиците», — объясняет Уиз.

Автор фото, Getty Images

Для некоторых методов вычисления только головы недостаточно, нужны еще и фломастеры

Невзирая на это, он полагает, что альтернативные методы умножения очень полезны.

«Я не думаю, что это полезно — сразу учить школьников умножению, заставляя их выучивать таблицу умножения, но не объясняя им при этом, откуда она взялась. Поскольку если они забудут одно число, то как они смогут продвинуться в решении задачи? Метод майя или японский метод необходим, потому что с его помощью вы можете понять общую структуру умножения, а это хорошее начало», — полагает Уиз.

Существует и ряд других способов умножения, например, русский или египетский, они не требуют дополнительных навыков рисования.

Как говорят специалисты, с которыми мы беседовали, все эти методы помогают лучше понять процесс умножения.

«Понятно, что все идет на пользу. Математика в сегодняшнем мире открыта как внутри, так и снаружи классной комнаты», — резюмирует Андреа Васкес, учительница математики из Аргентины.

Источник

Четыре способа умножения без калькулятора

Елена Синекович

Не любишь математику? Ты просто не умеешь ею пользоваться! На самом деле, это увлекательная наука. И наша подборка необычных методов умножения подтверждает это.

Умножай на пальцах, как купец

Этот метод позволяет умножать числа от 6 до 9. Для начала согни обе руки в кулаки. Затем на левой руке отогни столько пальцев, на сколько первый множитель больше числа 5. На правой проделай то же самое для второго множителя. Посчитай количество разогнутых пальцев и умножь сумму на десять. А теперь перемножь сумму загнутых пальцев левой и правой руки. Сложив обе суммы, получишь результат.

Пример. Умножим 6 на 7. Шесть больше пяти на один, значит на левой руке отгибаем один палец. А семь – на два, значит на правой – два пальца. В сумме – это три, а после умножения на 10 – 30. Теперь перемножим четыре загнутых пальца левой руки и три – правой. Получим 12. Сумма 30 и 12 даст 42.

Вообще-то здесь речь идет о простой таблице умножения, которую хорошо бы знать наизусть. Но этот метод хорош для самопроверки, да и пальцы размять полезно.

Умножай, как Ферроль

Этот способ получил название по фамилии немецкого инженера, который им пользовался. Метод позволяет быстро перемножить числа от 10 до 20. Если потренируешься, то сможешь делать это даже в уме.

Суть простая. В итоге всегда будет получаться трехзначное число. Так что сначала считаем единицы, потом – десятки, затем – сотни.

Пример. Умножим 17 на 16. Чтобы получить единицы, умножаем 7 на 6, десятки – складываем произведение 1 и 6 с произведением 7 и 1, сотни – умножаем 1 на 1. В итоге получим 42, 13 и 1. Для удобства запишем их в столбик и сложим. Вот и итог!

Умножай, как японец

Этот графический способ, которым пользуются японские школьники, позволяет легко перемножить двух- и даже трехзначные числа. Чтобы опробовать его, приготовь бумагу и ручку.

Пример. Умножим 32 на 143. Для этого нарисуем сетку: первое число отразим тремя и двумя линиями с отступом по горизонтали, а второе – одной, четырьмя и тремя линиями по вертикали. В местах пересечения линий поставим точки. В итоге у нас должно получиться четырехзначное число, поэтому условно разделим таблицу на 4 сектора. И пересчитаем точки, попавшие в каждый из них. Получаем 3, 14, 17 и 6. Чтобы получить ответ, лишние единички у 14 и 17 прибавим к предыдущему числу. Получим 4, 5 и 76 – 4576.

Умножай, как итальянец

Еще один интересный графический способ используется в Италии. Пожалуй, он проще японского: точно не запутаешься при переносе десятков. Чтобы перемножить большие числа с его помощью, нужно начертить сетку. По горизонтали сверху записываем первый множитель, а по вертикали справа – второй. При этом на каждую цифру должна приходиться одна клетка.

Теперь перемножим цифры каждого ряда на цифры каждой колонки. Результат запишем в клетку (разделенную надвое) на их пересечении. Если получилось однозначное число, то в верхнюю часть клетки пишем 0, а в нижнюю – полученный результат.

Осталось сложить все числа, оказавшиеся в диагональных полосках. Начинаем с нижней правой клетки. Десятки при этом прибавляем к единицам в соседнем столбике.

Вот как мы умножили 639 на 12.

Весело, правда? Нескучной тебе математики! И помни, что гуманитарии в ИТ тоже нужны!

Источник

Японский способ умножения чисел без калькулятора

В большинстве школ учат умножать цифры в столбик, но данная система подходит не всем детям. Есть дети, которым нужно показать наглядно, как это происходит.

У творческих людей, а также и у большинства девочек математика и вообще точные предметы не идут. При этом в обычной школе нет подхода к каждому ученику. Весь материал объясняется одинаково. Репетитор тоже, не всегда может объяснить как-то по-другому. Нужно преподносить школьный материал другим способом. В данной статье разбиваем стереотип умножения цифр в столбик и показываем новый способ умножения цифр по японской системе.

Умножение чисел быстро без калькулятора!

Как умножить 12 х 13?

1.Берём лист бумаги в клетку и цветные фломастеры. Записываем пример 12 х 13.

2.Горизонтально представляем цифру «12» в виде линий. Рисуем 1 полоску – это один. Спустя клеточки рисуем две полоски.

3.Теперь представляем цифру «13» в в виде линий вертикально.

4.В правом нижнем углу считаем точки пересечения двух линий. Получается цифра «6».

5.По диагонали считаем точки пересечения линий и складываем. Получается «5».

6.Остается верхний левый угол. Цифра «1».

7.Записываем результат с конца (это нижний правый угол). 12 х 13 = 156.

Рассмотрим ещё 1 пример. Как умножить 16 х 13?

8.Представляем первый ряд цифр. Рисуем линию, спустя клеточки рисуем 6 линий по горизонтали.

9.Рисуем одну линию по вертикали, спустя клеточки три линии – это цифра «13».

10.Считаем сколько точек пересечения? Получается «18».

11.Считаем точки по диагонали и складываем. Получается «9».

12.В левом верхнем углу цифра «1».

13.Начинаем записывать результат с конца. После равно отступаем место и пишем 8. Далее цифра 1 перекидывается к следующему ряду цифр и прибавляем к тому числу, которое указано. В ответ записываем «0», а цифру слева перекидываем в следующий ряд. Складываем. Записываем цифру «2» в ответ. Пример по математике 16 х 13 = 208.

В примерах всегда важна практика. Попробуем умножить сложные цифры.

Как умножить 132 х 213?

14.Рассмотрим умножение 3-ых чисел. Представляем числа, как мы показывали ранее, в виде линий.

15.Считаем точки пересечения в нижнем углу. Получается «6».

16.Берём ближайшую диагональ. Считаем, складываем и получается «11».

17.Далее считаем следующий ряд по диагонали. Ответ «10».

18.Далее следующий ряд. Цифра «7».

19.В верхнем углу цифра «2». Теперь считаем. После равно отступаем место и пишем последнюю цифру из нижнего угла. Записываем «6». Из следующего ряда записываем 1, а вторая единичка уходит в следующий ряд. Складываем. Записываем в ответ «1», а далее складываем первую цифру и следующий ряд. Пишем в ответ «8». Остается цифра «2». Пример по математике 132 х 213 = 28116.

Советуем потренироваться на разных примерах самостоятельно, а также посмотреть видео к описанию примера на нашем канале.

На сайте kak-sdelat-vse.com много полезной информации для детей и взрослых. Заходите, читайте и делитесь полезными ссылками с друзьями. Также, вы можете изучать английский язык бесплатно, посмотрите статьи в рубрике «изучение английского». Пополняйте ваш словарный запас и знания!

Видео.Японский способ умножения чисел?

Источник