Японский способ деления чисел

Старинные способы умножения

Презентация к уроку

Загрузить презентацию (411 кБ)

“Счёт и вычисления – основа порядка в голове”.
Песталоцци

Цель:

• Познакомиться со старинными приемами умножения.
• Расширить знания по различным приемам умножения.
• Научиться выполнять действия с натуральными числами, используя старинные способы умножения .

Содержание.

1. Старинный способ умножение на 9 на пальцах
2. Умножение методом Ферроля.
3. Японский способ умножения.
4. Итальянский способ умножения (“Сеткой”)
5. Русский способ умножения.
6. Индийский способ умножения.

Ход занятия

Актуальность использования приемов быстрого счета.

В современной жизни каждому человеку часто приходится выполнять огромное количество расчётов и вычислений. Поэтому цель моей работы – показать лёгкие, быстрые и точные методы счёта, которые не только помогут вам во время каких-либо расчётах, но вызовут немалое удивление у знакомых и товарищей, ведь свободное выполнение счётных операций в значительной степени может свидетельствовать о незаурядности вашего интеллекта. Основополагающим элементом вычислительной культуры являются сознательные и прочные вычислительные навыки. Проблема формирования вычислительной культуры актуальна для всего школьного курса математики, начиная с начальных классов, и требует не простого овладения вычислительными навыками, а использования их в различных ситуациях. Владение вычислительными умениями и навыками имеет большое значение для усвоения изучаемого материала, позволяет воспитывать ценные трудовые качества: ответственное отношение к своей работе, умение обнаруживать и исправлять допущенные в работе ошибки, аккуратное исполнение задания, творческое отношение к труду. Однако, в последнее время уровень вычислительных навыков, преобразований выражений имеет ярко выраженную тенденцию к снижению, учащиеся допускают массу ошибок при подсчетах, все чаще используют калькулятор, не мыслят рационально, что отрицательно сказывается на качестве обучения и уровне математических знаний учащихся в целом. Одной из составляющих вычислительной культуры является устный счёт, который имеет большое значение. Умение быстро и правильно произвести несложные вычисления “в уме” необходимо для каждого человека.

Старинные способы умножения чисел.

1. Старинный способ умножение на 9 на пальцах

Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9 x 3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9 x 3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.

2. Умножение методом Ферроля.

Для умножения единиц произведения переумножения перемножают единицы множителей, для получения десятков, умножают десятки одного на единицы другого и наоборот и результаты складывают, для получения сотен перемножают десятки. Методом Ферроля легко перемножать устно двухзначные числа от 10 до 20.

б) 1х4+2х1=6, пишем 6

3. Японский способ умножения

Такой прием напоминает умножение столбиком, но проводится довольно долго.

Использование приема. Допустим, нам надо умножить 13 на 24. Начертим следующий рисунок:

Этот рисунок состоит из 10 линий (количество может быть любым)

• Эти линии обозначают число 24 (2 линии, отступ, 4 линии)
• А эти линии обозначают число 13 (1 линия, отступ, 3 линии)

Теперь нужно сосчитать пересечения линий на всех четырех концах следующим способом:

(пересечения на рисунке указаны точками)

Количество пересечений:

• Верхний левый край: 2
• Нижний левый край: 6
• Верхний правый: 4
• Нижний правый: 12

1) Пересечения в верхнем левом крае (2) – первое число ответа

2) Сумма пересечений нижнего левого и верхнего правого краев (6+4) – второе число ответа

3) Пересечения в нижнем правом крае (12) – третье число ответа.

Получается: 2; 10; 12.

Т.к. два последних числа – двузначные и мы не можем их записать, то записываем только единицы, а десятки прибавляем к предыдущему.

4. Итальянский способ умножения (“Сеткой”)

В Италии, а также во многих странах Востока, этот способ приобрел большую известность.

Например, умножим 6827 на 345.

1. Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте.

2. Умножаем число каждого ряда последовательно на числа каждой колонки.

т.е.

• 6*3 = 18. Записываем 1 и 8
• 8*3 = 24. Записываем 2 и 4

Если при умножении получается однозначное число, записываем вверху 0, а внизу это число.

(Как у нас в примере при умножении 2 на 3 получилось 6. Вверху мы записали 0, а внизу 6)

3. Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.

5. Русский способ умножения.

Этот прием умножения использовался русскими крестьянами примерно 2-4 века назад, а разработан был еще в глубокой древности. Суть этого способа та:“На сколько мы делим первый множитель, на столько умножаем второй”.Вот пример: Нам нужно 32 умножить на 13. Вот как бы решили этот пример 3-4 века назад наши предки:

• 32 * 13 (32 делим на 2, а 13 умножаем на 2)
• 16 * 26 (16 делим на 2, а 26 умножаем на 2)
• 8 * 52 (и т.д.)
• 4 * 104
• 2 * 208
• 1 * 416 =416

Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат. Нетрудно понять, на чем этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение

Однако как поступить, если при этом приходится делить пополам число нечетное? Народный способ легко выходит из этого затруднения. Надо, — гласит правило, — в случае нечётного числа откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением. Практически это делают так, что все строки с четными левыми числами зачеркивают; остаются только те, которые содержат налево нечетное число. Приведем пример (звездочки указывают, что данную строку надо зачеркнуть):

• 19*17
• 9*34
• 4 *68*
• 2 *136*
• 1 *272

Сложив незачеркнутые числа, получаем вполне правильный результат:

• 17 + 34 + 272 = 323.

6. Индийский способ умножения.

Такой способ умножения использовали в Древней Индии.

Для умножения, например, 793 на 92 напишем одно число как множимое и под ним другое как множитель. Чтобы легче ориентироваться, можно использовать сетку (А) как образец.

Теперь умножаем левую цифру множителя на каждую цифру множимого, то есть, 9х7, 9х9 и 9х3. Полученные произведения пишем в сетку (Б), имея в виду следующие правила:

• Правило 1. Единицы первого произведения следует писать в той же колонке, что и множитель, то есть в данном случае под 9.
• Правило 2. Последующее произведения надо писать таким образом, чтобы единицы помещались в колонке непосредственно справа от предыдущего произведения.

Повторим весь процесс с другими цифрами множителя, следуя тем же правилам (С).

Затем складываем цифры в колонках и получаем ответ: 72956.

Как можно видеть, мы получаем большой список произведений. Индийцы, имевшие большую практику, писали каждую цифру не в соответствующую колонку, а сверху, насколько это было возможно. Затем они складывали цифры в колонках и получали результат.

Заключение

Мы вступили в новое тысячелетие! Грандиозные открытия и достижения человечества. Мы много знаем, многое умеем. Кажется чем-то сверхъестественным, что с помощью чисел и формул можно рассчитать полёт космического корабля, “экономическую — ситуацию” в стране, погоду на “завтра”, описать звучание нот в мелодии. Нам известно высказывание древнегреческого математика, философа, жившего в 4 веке д. н.э.- Пифагора — “Всё есть число!”.

Согласно философскому воззрению этого учёного и его последователей, числа управляют не только мерой и весом, но также всеми явлениями, происходящими в природе, и являются сущностью гармонии, царствующей в мире, душой космоса.

Описывая старинные способы вычислений и современные приёмы быстрого счёта, я попытался показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись.

“Кто с детских лет занимается математикой, тот развивает внимание, тренирует мозг, свою волю, воспитывает настойчивость и упорство в достижении цели”. (А.Маркушевич)

Источник

Умножение по-японски

В японских школах уроки математики сильно разнятся с теми, к которым мы привыкли в России. Есть в их школах нечто такое, что завораживает, заставляет удивиться и произнести:” Такое возможно?”. Интересно, почему так? С этим нам и придется разобраться.

Менталитет Японии сильно разнится с нашим. Поэтому многое, что присуще японской системе образования, нами было бы вряд ли принято и понято. Но все же у них есть, чему поучиться.

Естественно, что так же как и у нас, японские школьники учат таблицу умножения во втором-третьем классе. У нас этот процесс чаще похож на скучное заучивание цифр и их произведение. Помню свой то ли второй, то ли третий класс: нам дали задание выучить таблицу на каникулах, моя бабушка сходила на рынок, купила большой плакат с таблицей и каждые два часа заставляла меня повторять. Под таким напором и весь курс математики за неделю можно выучить. Но такой способ не очень приятный, да и не всегда рабочий.

В Японии дети учат особую рифмованную таблицу, которая имеет специфическое название — «kuku».Необычность этой системы заключается в запоминании таблицы на скорость. Там даже есть целые турниры со скоростным решением примеров и задач! Сначала дети практикуются в своем классе, потом перед всей школой. Слышали об олимпиадах в США, где дети в актовом зале должны быстро разобрать слова на буквы и звуки? Что-то такое есть в Японии, только с таблицей умножения.

Такая система эффективна благодаря своей соревновательной идеи. Ребенок чувствует азарт, хочет проявить себя и стремится быть лучшим среди своих одноклассников. Ведь каждому из нас нравится стремиться к победе!

Хотели бы иметь на стенке сертификат о лучшем знании таблицы умножения среди учеников 2 класса? Я бы хотел. 🙂

В Японии к ментальной арифметике относятся с любовью. Дети в полной мере развивают счет в уме с младших классов, но только после того, как научатся считать на специальной доске — абаке , собране или абакусе. Нашим языком — счеты. Наверное, у каждого из нас была эта доска дома, которой никто не пользовался с момента появления калькуляторов. И, кажется, я так и не научился ей тогда пользоваться.

Есть еще интереснее метод умножения в Японии, который даже в первом классе объясняют. Забавно, но в нем заучивание вовсе не требуется! Достаточно нарисовать несколько полосок на листке бумаги. Звучит странно и слишком легко. Когда узнал о нем поподробнее, даже спросил у знакого у Японии:”У вас правда это используют?” и получил одобряющий кивок, я решил сам проверить метод. Он оказался гениальным!

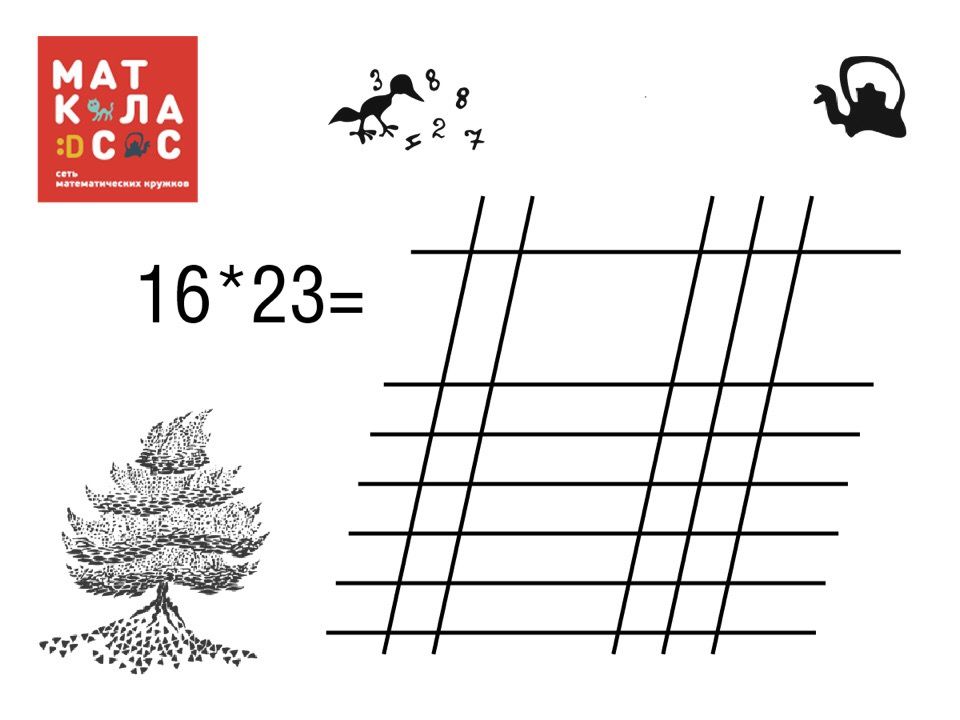
Как это работает: берутся два множителя. Допустим, это будет 16 и 23, как на картинке! Пускай по вертикали будет число 16. Мы берем и разбиваем число на части, как в первом классе нас учат делить слова на слоги. Вверху рисуем одну палочку, отступаем и внизу прорисовываем еще шесть. Таким образом мы изобразили число 16, но палочек всего семь? “Почему?” — спросите вы? Потому что мы разобрали 16 на 1 и 6. Далее по горизонтали прямо на этих линиях рисуем число 23, так же разбиваем его на 2 и 3, только отступаем не вниз, а вправо. И вот, мы видим, как у нас появляются своеобразные решеточки.

Теперь попробуем посчитать. Для начала считаем в левом верхнем углу. При соединении палочек (одной палочки от 16 и двух от 23) образуются точки, как если бы в плюсе + мы выделили серединку точкой, получается что там всего 2 точки. Дальше считаем таким же образом точки в нижнем левом углу и, внимание, в правом верхнем углу. Это число нужно сосчитать вместе! Получается число 15. И теперь считаем точки в правом нижнем углу, там получится 18. Складываем столбиком таким образом: Двойку ставим на первое место в первой строке. Во второй строке пишем 15 так, чтобы единица была под двойкой. И соответственно под числом пять второй строки должно начинаться число 18. Таким образом, восемь — это конец числа, один и пять складываем и получаем 6, и двойку соединяем с единицей. Правильный ответ 368! Проверьте сами, этот способ очень хороший, жаль что с большими числами по типу 99, будет не очень удобно считать.

Основная проблема такого решения — неудобства при счете больших чисел. Не каждый станет рисовать девяносто девять линий на других девяносто девяти. В Японии, когда умножение больших чисел будет необходимо, ученики уже будут знать стандартное умножение в столбик.

Но не все так гладко в японской системе образования. Плюсов у нее достаточно, но и минусы есть: высокая нагрузка на учеников младших классов, сильные требования к умению считать деньги и обращаться с ними. В некоторых школах учат цены в магазинах. Навыки полезные, спорить сложно, но в первом и втором классе. По сравнению с четвертым классом, это еще цветочки. 😀 Множители доходят до тысяч, а то и до миллионов.

Высокие требования не есть плохо, но и не есть хорошо. Стоит понимать, что в японских школах не только математика удосужилась углубленного изучения. Каждый предмет имеет свои специфичные методы, непривычные нам. Но и требования там жестче.Как говорилось в начале статьи, это один из ярких примеров разницы менталитетов.

Мы считаем, что полезное нужно чередовать с приятным. Что и делают наши педагоги на занятиях, давая им учебную и творческую свободы. На них ребенок сразу увидит разницу со школьными уроками: он не просто повторяет школьный курс, но и узнает что-то новое. Кружки и каникулярные программы — приключение в мир математических развлечений. Возможно наша математика и отличается от математики в Японии, но мы считаем, что она ничуть не хуже. 🙂

Источник