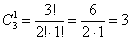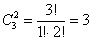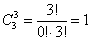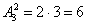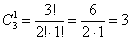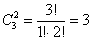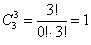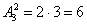- 1.3.1. Перестановки, сочетания и размещения без повторений
- Перестановки, сочетания и размещения без повторений
- Задачи по теме «Перестановки. Сочетания. Размещения»
- Решение комбинаторных задач по математике
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Безлимитный доступ к занятиям с онлайн-репетиторами
- Подарочные сертификаты
1.3.1. Перестановки, сочетания и размещения без повторений
Начнём с хвоста заголовка – что значит «без повторений»? Это значит, что в данном параграфе будут рассматриваться множества, которые состоят из различных объектов, либо которые считаются таковыми по смыслу задачи.
Представьте, что перед вами на столе слева направо выложены:
яблоко / груша / банан
Вопрос первый: сколькими способами их можно переставить?
Одна комбинация уже записана выше и с остальными проблем не возникает:
яблоко / банан / груша
груша / яблоко / банан
груша / банан / яблоко
банан / яблоко / груша
банан / груша / яблоко
Итого: 6 комбинаций или 6 перестановок.
Хорошо, здесь не составило особого труда перечислить все возможные случаи, но как быть, если предметов больше? Уже с четырьмя различными фруктами количество комбинаций значительно возрастёт! Пожалуйста, откройте Приложение Основные формулы комбинаторики и в пункте № 2 найдите формулу количества перестановок. Никаких мучений – 3 объекта можно переставить: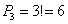 
способами.
Вопрос второй: сколькими способами можно выбрать а) один фрукт, б) два фрукта, в) три фрукта, г) хотя бы один фрукт?
а) Один фрукт можно выбрать, очевидно, тремя способами – взять либо яблоко, либо грушу, либо банан. Формальный подсчёт проводится по формуле количества сочетаний (см. тот же п.2 Приложения): 
Запись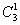 
следует читать и понимать так: «сколькими способами можно выбрать 1 фрукт из трёх?».
б) Перечислим все возможные сочетания двух фруктов:
яблоко и груша;
яблоко и банан;
груша и банан.
Количество комбинаций легко проверить по той же формуле: 
Запись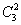 
понимается аналогично: «сколькими способами можно выбрать 2 фрукта из трёх?».
в) И, наконец, три фрукта можно выбрать единственным способом:
Следует отметить, что формула количества сочетаний сохраняет смысл и для пустой выборки:
способом можно выбрать ни одного фрукта – собственно, ничего не взять и всё. Но это явно не про студенток J
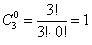
г) Сколькими способами можно взять хотя бы один фрукт? Условие «хотя бы один» подразумевает, что нас устраивает 1 фрукт (любой) или 2 любых фрукта (любые) или все 3 фрукта:
способами можно выбрать хотя бы один фрукт.
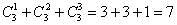
…внимательные читатели уже кое о чём догадались. Но о смысле знака «плюс» позже.
И для ответа на третий вопрос мне требуется два добровольца…, ну что же, раз никто не хочет, тогда буду вызывать к доске =)
Вопрос третий: сколькими способами можно раздать по одному фрукту Даше и Наташе?
Для того чтобы раздать два фрукта, сначала нужно их выбрать. Согласно пункту «бэ» предыдущего вопроса, сделать это можно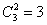 
способами, перепишу их заново:
яблоко и груша;
яблоко и банан;
груша и банан.
Но комбинаций сейчас будет в два раза больше. Рассмотрим, например, первую пару фруктов:
яблоком можно угостить Дашу, а грушей – Наташу;
либо наоборот – груша достанется Даше, а яблоко – Наташе.
И такая перестановка возможна для каждой пары фруктов.
В данном случае работает формула количества размещений: 
Она отличается от формулы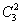 
тем, что учитывает не только количество способов, которым можно выбрать несколько объектов, но и все перестановки объектов в каждой возможной выборке. Так, в рассмотренном примере, важно не только то, что можно просто выбрать, например, грушу и банан, но и то, как они будут распределены (размещены) между Дашей и Наташей.
Пожалуйста, ещё раз внимательно перечитайте пункт № 2 Приложения Основные формулы комбинаторики и постарайтесь хорошо уяснить разницу между перестановками, сочетаниями и размещениями. В простых случаях легко пересчитать все возможные комбинации вручную, но чаще всего это становится трудноподъёмной задачей, именно поэтому и нужно понимать смысл формул.
Теперь остановимся на каждой комбинации подробнее:
Полную и свежую версию этой книги в pdf-формате ,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Источник
Перестановки, сочетания и размещения без повторений
Не пугайтесь малопонятных терминов, тем более, некоторые из них действительно не очень удачны. Начнём с хвоста заголовка – что значит «без повторений»? Это значит, что в данном параграфе будут рассматриваться множества, которые состоят из различных объектов. Например, представьте, что перед вами на столе яблоко, груша и банан. Выкладываем фрукты слева направо в следующем порядке:
яблоко / груша / банан
Вопрос первый: сколькими способами их можно переставить?
Одна комбинация уже записана выше и с остальными проблем не возникает:
яблоко / банан / груша
груша / яблоко / банан
груша / банан / яблоко
банан / яблоко / груша
банан / груша / яблоко
Итого: 6 комбинаций или 6 перестановок.
Хорошо, здесь не составило особого труда перечислить все возможные случаи, но как быть, если предметов больше? Уже с четырьмя различными фруктами количество комбинаций значительно возрастёт!
Пожалуйста, откройте справочный материал Основные формулы комбинаторики, найдите формулу количества перестановок.
Никаких мучений – 3 объекта можно переставить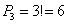 
способами.
Вопрос второй: сколькими способами можно выбрать а) один фрукт, б) два фрукта, в) три фрукта, г) хотя бы один фрукт?
а) Один фрукт можно выбрать, очевидно, тремя способами – взять либо яблоко, либо грушу, либо банан. Формальный подсчёт проводится по формуле количества сочетаний: 
Запись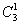 
в данном случае следует понимать так: «сколькими способами можно
выбрать 1 фрукт из трёх?»
б) Перечислим все возможные сочетания двух фруктов:
яблоко и груша;
яблоко и банан;
груша и банан.
Количество комбинаций легко проверить по той же формуле: 
Запись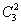 
понимается аналогично: «сколькими способами можно выбрать 2 фрукта из трёх?».
в) И, наконец, три фрукта можно выбрать единственным способом: 
Кстати, формула количества сочетаний сохраняет смысл и для пустой выборки:
способом можно выбрать ни одного фрукта – собственно, ничего не взять и всё.
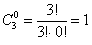
г) Сколькими способами можно взять хотя бы один фрукт? Условие «хотя бы один» подразумевает, что нас устраивает 1 фрукт (любой) или 2 любых фрукта или все 3 фрукта:
способами можно выбрать хотя бы один фрукт.
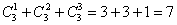
Вопрос третий: сколькими способами можно раздать по одному фрукту Даше и Наташе?
Для того чтобы раздать два фрукта, сначала нужно их выбрать. Согласно пункту «бэ» предыдущего вопроса, сделать это можно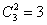 
способами, перепишу их заново:
яблоко и груша;
яблоко и банан;
груша и банан.
Но комбинаций сейчас будет в два раза больше. Рассмотрим, например, первую пару фруктов:
яблоком можно угостить Дашу, а грушей – Наташу;
либо наоборот – груша достанется Даше, а яблоко – Наташе.
И такая перестановка возможна для каждой пары фруктов.
В данном случае работает формула количества размещений: 
Она отличается от формулы 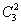тем, что учитывает не только количество способов, которым можно выбрать несколько объектов, но и все перестановки объектов в каждой возможной выборке. Так, в рассмотренном примере, важно не только то, что можно просто выбрать, например, грушу и банан, но и то, как они будут распределены (размещены) между Дашей и Наташей.
Также напоминаю, что сейчас речь идёт о множестве с различными объектами, и если яблоко/грушу/банан заменить на 3 яблока или даже на 3 очень похожих яблока, то в контексте рассмотренной задачи они всё равно будут считаться различными.
Остановимся на каждом виде комбинаций подробнее:
Источник
Задачи по теме «Перестановки. Сочетания. Размещения»
 Перестановки №1. На столе яблоко, груша и банан. Сколькими способами их можно переставить? Размещения №2. Сколькими способами можно раздать по одному фрукту Даше и Наташе? Для того чтобы раздать два фрукта, сначала нужно их выбрать. Сделать это можно способами: яблоко и груша; яблоко и банан; груша и банан. Но комбинаций сейчас будет в два раза больше. Рассмотрим, например, первую пару фруктов: яблоком можно угостить Дашу, а грушей – Наташу; либо наоборот – груша достанется Даше, а яблоко – Наташе. И такая перестановка возможна для каждой пары фруктов. Сочетания №3. Сколькими способами можно выбрать а) один фрукт, б) два фрукта, в) три фрукта, г) хотя бы один фрукт из трех? 2 элемента из 3 элементов формула количества сочетаний: №4. В ящике находится 15 деталей. Сколькими способами можно взять 4 детали? 4 элемента из 15 элементов №5. Боря, Дима и Володя сели играть в «очко». Сколькими способами им можно сдать по одной карте? (колода содержит 36 карт) 3 элемента из 36 элементов №6. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах? 4 элемента для 9 ячеек №7. Сколько двузначных чисел можно составить из цифр 1. 3, 5, 8, 9 так, чтобы в каждом числе не было одинаковых цифр? 5 элементов для 2 ячеек №8. Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно выбрать двух человек одного пола? №9. Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно составить пару из юноши и девушки? №10. Группу из 20 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 3 человека, во вторую — 5 и в третью — 12. Сколькими способами это можно сделать.
Источник Решение комбинаторных задач по математике
Описание презентации по отдельным слайдам: Рано или поздно всякая правильная математическая идея находит применение в том или ином деле. (А.Н. Крылов) Какой смайлик соответствует твоему настроению на начало урока Задача У кассы кинотеатра стоят четверо ребят. У двух из них сторублевые купюры, у других двух – пятидесятирублевые. Билет в кино стоит 50 рублей. В начале продажи касса пуста. Как должны расположиться ребята, чтобы никому не пришлось ждать сдачи? 50 Задача У кассы кинотеатра стоят четверо ребят. У двух из них сторублевые купюры, у других двух – пятидесятирублевые. Билет в кино стоит 50 рублей. В начале продажи касса пуста. Как должны расположиться ребята, чтобы никому не пришлось ждать сдачи? 50 50 рублей, 100 рублей, 50 рублей, 100 рублей; 50 рублей, 50 рублей, 100 рублей, 100 рублей . Составьте из полосок флаг Российской Федерации. Составьте из полосок флаг Российской Федерации. Что означает каждый цвет нашего флага? Составьте из полосок флаг Российской Федерации. Что означает каждый цвет нашего флага? ( белый – мир, чистота, совершенство; синий – цвет веры и верности; красный – энергия, сила, кровь, пролитую за Отечество.) Поменяйте местами полоски Нидерланды Франция Югославия Перебор возможных вариантов: КБС КСБ БСК БКС СБК СКБ красный белый синий Б С С К Б К Дерево вариантов: 3 х 2 х 1=6 Решение комбинаторных задач Слово «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять». Термин «комбинаторика» был введён знаменитым Готфридом Вильгельмом Лейбницем, — всемирно известным немецким учёным. Занимался идеями комбинаторного искусства. Сколько существует вариантов покупки одной розы, если продают 3 алые, 2 белые и 4 желтые розы? 9 способов Задача №1. Важно помнить, что выбирается не просто красная, белая или желтая роза, а одна конкретная роза: эта красная или эта белая, или эта желтая роза. Правило суммы Если некоторый элемент А можно выбрать n способами, а элемент В – m способами, то выбор «либо А, либо В» можно сделать n + m способами. A – n способов В – m способов А или В – (n + m)способов Задача №2. В столовой есть 2 первых блюда и 3 вторых. Сколько различных вариантов обеда из 2 блюд можно заказать? Первое блюдо: Второе блюдо: 3 + 3 = 2 ∙ 3 = 6 способов 2 3 Правило произведения Если некоторый элемент А можно выбрать n способами, а элемент В – m способами, то пару А и В можно выбрать n ∙ m способами. A – n способов В – m способов А и В – (n ∙ m)способов На блюде лежат 8 яблок, 3 груши и 4 апельсина. Задача №3. а) Сколькими способами можно взять один плод? 8 + 3 + 4 = 15 способов б) Сколькими способами можно взять: яблоко с грушей яблоко с апельсином грушу с апельсином яблоко, грушу и апельсин 8 · 3 = 24 способа 8 · 4 = 32 способа 3 · 4 = 12 способов Выбирается 1 плод. Выбирается 2 или 3 плода. 8 · 3 · 4 = 96 способов На блюде лежат 8 яблок, 3 груши и 4 апельсина. Задача №3. в) Сколькими способами можно взять два фрукта с разными названиями? Применяются оба правила. Выбирается пара. Пара рассматривается как единое целое. 8 · 3 + 8 · 4 + 3 · 4 = 24 + 32 +12 = 68 способов Сколько различных двузначных чисел можно составить, используя цифры 1,4, и 7, если цифры могут повторяться. Задача №5. 1 способ (перебор) 1 7 4 11 14 17 41 44 47 71 74 77 Ответ: 9 чисел Сколько различных двузначных чисел можно составить, используя цифры 1,4, и 7, если цифры могут повторяться. Задача №5. 2 способ (построение дерева различных вариантов) 4 7 4 1 1 7 1 цифра 2 цифра 4 1 7 4 1 7 Ответ: 9 чисел 11 14 17 41 44 47 71 74 77 Задача Квартет Проказница Мартышка Осёл, Козёл, Да косолапый Мишка Затеяли играть квартет … Стой, братцы стой! – Кричит Мартышка, — погодите! Как музыке идти? Ведь вы не так сидите… И так, и этак пересаживались – опять музыка на лад не идет. Вот пуще прежнего пошли у них разборы И споры, Кому и как сидеть… Сколькими способами можно рассадить четырех музыкантов? Решение: Здесь n=4, поэтому способов «усесться чинно в ряд» имеется P = 1 * 2 * 3 * 4 = 24 Я всё понял, у меня всё получалось! Мне не всё удалось, придется дома подольше посидеть Мне было очень трудно и непонятно
Курс повышения квалификации Дистанционное обучение как современный формат преподавания
Курс повышения квалификации Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Тема урока: Решение комбинаторных задач в 5 класс Цель урока : сформулировать первоначальные навыки решения комбинаторных задач. § Развитие умения решать комбинаторные задачи ; § Выработка умения применять математическую теорию в конкретных ситуациях. § Развитие умения самостоятельно выбирать способ решения и умения обосновать выбор; § Развитие умения решать задачи путём только логических рассуждений; § Развитие коммуникативных и творческих способностей учащихся; § Развитие умения делать выбор рационального способа кодирования. § Прививать сознательное отношение к труду; § Воспитывать чувство ответственности за качество и результат выполняемой работы; § Прививать сознательное отношение к труду. Номер материала: 101907 Международная дистанционная олимпиада Осень 2021 Не нашли то что искали? Оставьте свой комментарийАвторизуйтесь, чтобы задавать вопросы. Безлимитный доступ к занятиям с онлайн-репетиторамиВыгоднее, чем оплачивать каждое занятие отдельно
Правительство предложило потратить до 1 млрд рублей на установку флагов РФ у школ Время чтения: 1 минута
В России выбрали топ-10 вузов по работе со СМИ и контентом Время чтения: 3 минуты
Российский совет олимпиад школьников намерен усилить требования к олимпиадам Время чтения: 2 минуты
Минпросвещения разрабатывает образовательный минимум для подготовки педагогов Время чтения: 2 минуты
В проекте КоАП отказались от штрафов для школ Время чтения: 2 минуты
Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года Время чтения: 1 минута Подарочные сертификатыОтветственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи. Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов. Источник |
