1.3.1. Перестановки, сочетания и размещения без повторений
Начнём с хвоста заголовка – что значит «без повторений»? Это значит, что в данном параграфе будут рассматриваться множества, которые состоят из различных объектов, либо которые считаются таковыми по смыслу задачи.
Представьте, что перед вами на столе слева направо выложены:
яблоко / груша / банан
Вопрос первый: сколькими способами их можно переставить?
Одна комбинация уже записана выше и с остальными проблем не возникает:
яблоко / банан / груша
груша / яблоко / банан
груша / банан / яблоко
банан / яблоко / груша
банан / груша / яблоко
Итого: 6 комбинаций или 6 перестановок.
Хорошо, здесь не составило особого труда перечислить все возможные случаи, но как быть, если предметов больше? Уже с четырьмя различными фруктами количество комбинаций значительно возрастёт! Пожалуйста, откройте Приложение Основные формулы комбинаторики и в пункте № 2 найдите формулу количества перестановок. Никаких мучений – 3 объекта можно переставить: 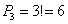
Вопрос второй: сколькими способами можно выбрать а) один фрукт, б) два фрукта, в) три фрукта, г) хотя бы один фрукт?
а) Один фрукт можно выбрать, очевидно, тремя способами – взять либо яблоко, либо грушу, либо банан. Формальный подсчёт проводится по формуле количества сочетаний (см. тот же п.2 Приложения):
Запись 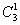
б) Перечислим все возможные сочетания двух фруктов:
яблоко и груша;
яблоко и банан;
груша и банан.
Количество комбинаций легко проверить по той же формуле:
Запись 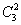
в) И, наконец, три фрукта можно выбрать единственным способом:
Следует отметить, что формула количества сочетаний сохраняет смысл и для пустой выборки:
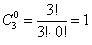
г) Сколькими способами можно взять хотя бы один фрукт? Условие «хотя бы один» подразумевает, что нас устраивает 1 фрукт (любой) или 2 любых фрукта (любые) или все 3 фрукта:
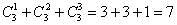
…внимательные читатели уже кое о чём догадались. Но о смысле знака «плюс» позже.
И для ответа на третий вопрос мне требуется два добровольца…, ну что же, раз никто не хочет, тогда буду вызывать к доске =)
Вопрос третий: сколькими способами можно раздать по одному фрукту Даше и Наташе?
Для того чтобы раздать два фрукта, сначала нужно их выбрать. Согласно пункту «бэ» предыдущего вопроса, сделать это можно 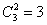
яблоко и груша;
яблоко и банан;
груша и банан.
Но комбинаций сейчас будет в два раза больше. Рассмотрим, например, первую пару фруктов:
яблоком можно угостить Дашу, а грушей – Наташу;
либо наоборот – груша достанется Даше, а яблоко – Наташе.
И такая перестановка возможна для каждой пары фруктов.
В данном случае работает формула количества размещений:
Она отличается от формулы 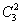
Пожалуйста, ещё раз внимательно перечитайте пункт № 2 Приложения Основные формулы комбинаторики и постарайтесь хорошо уяснить разницу между перестановками, сочетаниями и размещениями. В простых случаях легко пересчитать все возможные комбинации вручную, но чаще всего это становится трудноподъёмной задачей, именно поэтому и нужно понимать смысл формул.
Теперь остановимся на каждой комбинации подробнее:
Полную и свежую версию этой книги в pdf-формате ,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Источник
Перестановки, сочетания и размещения без повторений



Не пугайтесь малопонятных терминов, тем более, некоторые из них действительно не очень удачны. Начнём с хвоста заголовка – что значит «без повторений»? Это значит, что в данном параграфе будут рассматриваться множества, которые состоят из различных объектов. Например, представьте, что перед вами на столе яблоко, груша и банан. Выкладываем фрукты слева направо в следующем порядке:
яблоко / груша / банан
Вопрос первый: сколькими способами их можно переставить?
Одна комбинация уже записана выше и с остальными проблем не возникает:
яблоко / банан / груша
груша / яблоко / банан
груша / банан / яблоко
банан / яблоко / груша
банан / груша / яблоко
Итого: 6 комбинаций или 6 перестановок.
Хорошо, здесь не составило особого труда перечислить все возможные случаи, но как быть, если предметов больше? Уже с четырьмя различными фруктами количество комбинаций значительно возрастёт!
Пожалуйста, откройте справочный материал Основные формулы комбинаторики, найдите формулу количества перестановок.
Никаких мучений – 3 объекта можно переставить 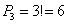
Вопрос второй: сколькими способами можно выбрать а) один фрукт, б) два фрукта, в) три фрукта, г) хотя бы один фрукт?
а) Один фрукт можно выбрать, очевидно, тремя способами – взять либо яблоко, либо грушу, либо банан. Формальный подсчёт проводится по формуле количества сочетаний:
Запись 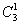
выбрать 1 фрукт из трёх?»
б) Перечислим все возможные сочетания двух фруктов:
яблоко и груша;
яблоко и банан;
груша и банан.
Количество комбинаций легко проверить по той же формуле:
Запись 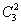
в) И, наконец, три фрукта можно выбрать единственным способом:
Кстати, формула количества сочетаний сохраняет смысл и для пустой выборки:
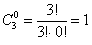
г) Сколькими способами можно взять хотя бы один фрукт? Условие «хотя бы один» подразумевает, что нас устраивает 1 фрукт (любой) или 2 любых фрукта или все 3 фрукта:
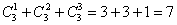
Вопрос третий: сколькими способами можно раздать по одному фрукту Даше и Наташе?
Для того чтобы раздать два фрукта, сначала нужно их выбрать. Согласно пункту «бэ» предыдущего вопроса, сделать это можно 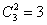
яблоко и груша;
яблоко и банан;
груша и банан.
Но комбинаций сейчас будет в два раза больше. Рассмотрим, например, первую пару фруктов:
яблоком можно угостить Дашу, а грушей – Наташу;
либо наоборот – груша достанется Даше, а яблоко – Наташе.
И такая перестановка возможна для каждой пары фруктов.
В данном случае работает формула количества размещений:
Она отличается от формулы 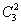
Также напоминаю, что сейчас речь идёт о множестве с различными объектами, и если яблоко/грушу/банан заменить на 3 яблока или даже на 3 очень похожих яблока, то в контексте рассмотренной задачи они всё равно будут считаться различными.
Остановимся на каждом виде комбинаций подробнее:
Источник
Задачи по теме «Перестановки. Сочетания. Размещения»
 Перестановки №1. На столе яблоко, груша и банан. Сколькими способами их можно переставить? Размещения №2. Сколькими способами можно раздать по одному фрукту Даше и Наташе? Для того чтобы раздать два фрукта, сначала нужно их выбрать. Сделать это можно способами: яблоко и груша; яблоко и банан; груша и банан. Но комбинаций сейчас будет в два раза больше. Рассмотрим, например, первую пару фруктов: яблоком можно угостить Дашу, а грушей – Наташу; либо наоборот – груша достанется Даше, а яблоко – Наташе. И такая перестановка возможна для каждой пары фруктов. Сочетания №3. Сколькими способами можно выбрать а) один фрукт, б) два фрукта, в) три фрукта, г) хотя бы один фрукт из трех? 2 элемента из 3 элементов формула количества сочетаний: №4. В ящике находится 15 деталей. Сколькими способами можно взять 4 детали? 4 элемента из 15 элементов №5. Боря, Дима и Володя сели играть в «очко». Сколькими способами им можно сдать по одной карте? (колода содержит 36 карт) 3 элемента из 36 элементов №6. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах? 4 элемента для 9 ячеек №7. Сколько двузначных чисел можно составить из цифр 1. 3, 5, 8, 9 так, чтобы в каждом числе не было одинаковых цифр? 5 элементов для 2 ячеек №8. Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно выбрать двух человек одного пола? №9. Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно составить пару из юноши и девушки? №10. Группу из 20 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 3 человека, во вторую — 5 и в третью — 12. Сколькими способами это можно сделать.
Источник Перестановки, сочетания и размещения без повторенийЗадачи по комбинаторике. Примеры решений Автор: Емелин Александр Для вычисления вероятностей событий необходимо разобраться с основными понятиями комбинаторики. Следует отметить, что комбинаторика является самостоятельным разделом высшей математики (а не частью ТВ). Нам достаточно небольшой доли теоретических знаний, которые мы рассмотрим ниже, и познакомимся с решением типовых комбинаторных задач. В узком смысле комбинаторика – это подсчёт различных комбинаций, которые можно составить из некоторого множества дискретных объектов. Под объектами понимаются какие-либо обособленные предметы или живые существа – люди, звери, грибы, растения, насекомые и т.д. При этом комбинаторику совершенно не волнует, что множество состоит из тарелки манной каши, паяльника и болотной лягушки. Принципиально важно, что эти объекты поддаются перечислению – их три (дискретность) и существенно то, что среди них нет одинаковых. Предварительно введем новое важное для нас понятие: факториал. Факториал – это произведение всех натуральных чисел от 1 до п. Обозначают п! ичитают: п — факториал.
Например, 6! = 720, 7! = 5040. Объясните, как получены данные равенства. Вычислим значение выражения: Теперь перейдем к комбинациям. Самыми распространёнными видами комбинаций являются перестановки объектов, их выборка из множества (сочетание) и распределение (размещение). Перестановки, сочетания и размещения без повторений Начнём с хвоста заголовка – что значит «без повторений»? Это значит, что в данной статье будем рассматривать множества, которые состоят из различных объектов. Представьте, что перед вами на столе лежат яблоко, груша и банан (при наличии таковых ситуацию можно смоделировать и реально). Выкладываем фрукты слева направо в следующем порядке: яблоко / груша / банан Вопрос первый: сколькими способами их можно переставить? Одна комбинация уже записана выше и с остальными проблем не возникает: яблоко / банан / груша Итого: 6 комбинаций или 6 перестановок. Хорошо, здесь не составило особого труда перечислить все возможные случаи. Но как быть, если предметов больше? Уже с четырьмя различными фруктами количество комбинаций значительно возрастёт! Попробуйте их составить самостоятельно. Получится 24 различных комбинаций. А чтобы составить все комбинации из 5 фруктов, то потребуется достаточно много времени, чтобы их записать. Пожалуйста, откройте справочный материал Основные формулы комбинаторики (методичку удобно распечатать) и в пункте №2 найдите формулу количества перестановок. Никаких мучений – 3 объекта можно переставить Р3 = 3! = 6 способами. Вопрос второй: сколькими способами можно выбрать а) один фрукт, б) два фрукта, в) три фрукта, г) хотя бы один фрукт? а) Один фрукт можно выбрать, очевидно, тремя способами – взять либо яблоко, либо грушу, либо банан. Формальный подсчёт проводится по формуле количества сочетаний: Запись б) Перечислим все возможные сочетания двух фруктов: яблоко и груша; Количество комбинаций легко проверить по той же формуле: в) И, наконец, три фрукта можно выбрать единственным способом: Кстати, формула количества сочетаний сохраняет смысл и для пустой выборки: г) Сколькими способами можно взять хотя бы один фрукт? Условие «хотя бы один» подразумевает, что нас устраивает 1 фрукт (любой) или 2 любых фрукта или все 3 фрукта: Читатели, внимательно изучившие вводный урок по теории вероятностей, уже кое о чём догадались. Но о смысле знака «плюс» позже. Вопрос третий: сколькими способами можно раздать по одному фрукту Даше и Наташе? Для того чтобы раздать два фрукта, сначала нужно их выбрать. Согласно пункту «бэ» предыдущего вопроса, сделать это можно яблоко и груша; Но комбинаций сейчас будет в два раза больше. Рассмотрим, например, первую пару фруктов: И такая перестановка возможна для каждой пары фруктов. В данном случае работает формула количества размещений: Пожалуйста, внимательно прочитайте Основные формулы комбинаторики и постарайтесь хорошо уяснить разницу между перестановками, сочетаниями и размещениями. В простейших случаях можно пересчитать все возможные комбинации вручную, но чаще всего это становится неподъемной задачей, именно поэтому и нужно понимать смысл формул. Остановимся на каждом виде комбинаций подробнее: Перестановки Перестановками называют комбинации, состоящие из одних и тех же n различных объектов и отличающиеся только порядком их расположения. Количество всех возможных перестановок выражается формулой Рn = n!. Отличительной особенностью перестановок является то, что в каждой из них участвуетВСЁ множество, то есть, всеn объектов. Сколькими способами можно рассадить 5 человек за столом? Решение: используем формулу количества перестановок: Р5 = 5! = 1 × 2 × 3 × 4 × 5 = 120. Ответ: 120 способами Невероятно, но факт. Обратите внимание, что здесь не имеет значения круглый ли стол, квадратный, или вообще все люди сели Сколько четырёхзначных чисел можно составить из четырёх карточек с цифрами 0, 5, 7, 9? Для того чтобы составить четырёхзначное число нужно задействовать все четыре карточки (цифры на которых различны!), и это очень важная предпосылка для применения формулы Рn = n!. Очевидно, что, переставляя карточки, мы будем получать различные четырёхзначные числа. … Стоп, а всё ли тут в порядке? Хорошенько подумайте над задачей! Вообще, это характерная черта комбинаторных и вероятностных задач – в них НУЖНО ДУМАТЬ. И зачастую думать по-житейски, как, например, в разборе вступительного примера с фруктами. Решение и ответ в конце урока. Сочетания В учебниках обычно даётся лаконичное и не очень понятное определение сочетаний, поэтому, в данная ниже формулировка будет не особо рациональной, но, надеюсь, доходчивой. Сочетаниями называют различные комбинации из m объектов, которые выбраны из множества n различных объектов, и которые отличаются друг от друга хотя бы одним объектом. Иными словами, отдельно взятое сочетание – это уникальная выборка из m элементов, в которой не важен их порядок (расположение). Общее же количество таких уникальных сочетаний рассчитывается по формуле: В ящике находится 15 деталей. Сколькими способами можно взять 4 детали? Решение: прежде всего, снова обращаю внимание на то, что по логике условия детали считаются различными– даже если они на самом деле однотипны и визуально одинаковы В задаче речь идёт о выборке из 4-х деталей, в которой не имеет значения их «дальнейшая судьба» – грубо говоря, «просто выбрали 4 штуки и всё». Таким образом, у нас имеют место сочетания деталей. Считаем их количество: Здесь, конечно же, не нужно ворочать огромные числа 11! = 39916800, 15! = 1307674368000. 1365 способами можно взять 4 детали из ящика. Ещё раз: что это значит? Это значит, что из набора 15-ти различных деталей можно составить одну тысячу триста шестьдесят пять уникальных сочетания 4-х деталей. То есть, каждая такая комбинация из 4-х деталей будет отличаться от других комбинаций хотя бы одной деталью. Ответ: 1365 способов Формуле Применительно к разобранной задаче: Сколькими способами из колоды в 36 карт можно выбрать 3 карты? Это пример для самостоятельного решения. Чем приятны многие комбинаторные задачи, так это краткостью – главное, разобраться в сути. Размещения Или «продвинутые» сочетания. Размещениями называют различные комбинации из k объектов, которые выбраны из множества n различных объектов, и которые отличаются друг от друга как составом объектов в выборке, так и их порядком. Количество размещений рассчитывается по формуле Данная формула может быть преобразована и записана и в таком виде: Боря, Дима и Володя сели играть в «очко». Сколькими способами им можно сдать по одной карте? (колода содержит 36 карт) Решение: ситуация похожа на предыдущую задачу, но отличается тем, что здесь важно не только то, какие три карты будут извлечены из колоды, но и то, КАК они будут распределены между игроками. По формуле размещений: Есть и другая схема решения, которая, с моей точки зрения, даже понятнее. Рассмотрим ее. Первый шаг: Второй шаг: теперь давайте рассмотрим, какую-нибудь одну из семи тысяч ста сорока комбинаций, например: король пик (КП), девятка червей (9Ч), семерка червей (7Ч). Выражаясь комбинаторной терминологией, эти 3 карты можно «переставить» между Борей, Димой и Володей Р3 = 3! = 6 способами: КП, 9Ч, 7Ч; Такое количество перестановок имеется для любого уникального набора из 3-х карт. А таких наборов, не забываем, мы насчитали По существу, получилась наглядная проверка формулы Ответ: 42840 способов. В студенческой группе 23 человека. Сколькими способами можно выбрать старосту и его заместителя? Задача о «размещении» должностей в коллективе встречается очень часто. Краткое решение и ответ в конце урока. Источник |

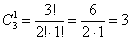
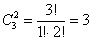
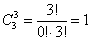
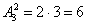



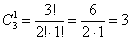
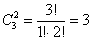
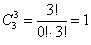
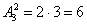
 . Объясните, как выполнены вычисления.
. Объясните, как выполнены вычисления.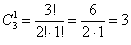
 в данном случае следует понимать так: «число способов, которыми можно выбрать один фрукт из трёх»
в данном случае следует понимать так: «число способов, которыми можно выбрать один фрукт из трёх»
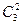 понимается аналогично: «число способов, которыми можно выбрать два фрукта из трёх»
понимается аналогично: «число способов, которыми можно выбрать два фрукта из трёх»
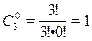 способом можно выбрать ни одного фрукта – собственно, ничего не взять и всё.
способом можно выбрать ни одного фрукта – собственно, ничего не взять и всё. = 3 + 3 + 1 = 7 способами можно выбрать хотя бы один фрукт.
= 3 + 3 + 1 = 7 способами можно выбрать хотя бы один фрукт. способами, перепишу их заново:
способами, перепишу их заново:


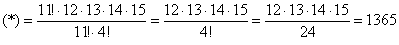
 ,
,  ,
,  ,
,  .
. – единственным способом можно взять ни одной детали;
– единственным способом можно взять ни одной детали; – способами можно взять 1 деталь (любую из 15-ти);
– способами можно взять 1 деталь (любую из 15-ти); – способами можно взять 14 деталей (при этом какая-то одна из 15-ти останется в ящике);
– способами можно взять 14 деталей (при этом какая-то одна из 15-ти останется в ящике);  – единственным способом можно взять все пятнадцать деталей.
– единственным способом можно взять все пятнадцать деталей. =n (n – 1) (n – 1)… (n – k +1).
=n (n – 1) (n – 1)… (n – k +1).
 =36 × 35 × 34 = 42840 способами можно раздать 3 карты игрокам.
=36 × 35 × 34 = 42840 способами можно раздать 3 карты игрокам. способами можно извлечь 3 карты из колоды.
способами можно извлечь 3 карты из колоды. . Не нужно быть профессором, чтобы понять, что найденное количество сочетаний следует умножить на шесть и тогда мы получим количество всех способов раздачи по одной карте трем игрокам. Итак:
. Не нужно быть профессором, чтобы понять, что найденное количество сочетаний следует умножить на шесть и тогда мы получим количество всех способов раздачи по одной карте трем игрокам. Итак:  способами можно сдать по одной карте 3-м игрокам. Этот результат равен тому, который получили, решая задачу по формуле размещения.
способами можно сдать по одной карте 3-м игрокам. Этот результат равен тому, который получили, решая задачу по формуле размещения. . Конкретный смысл этой формуле более подробно рассмотрен в конце решения задачи 8.
. Конкретный смысл этой формуле более подробно рассмотрен в конце решения задачи 8.


