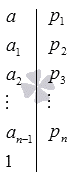Взаимно простые множители 4 способа

Взаимно простые числа

О чем эта статья:

5 класс, 6 класс

Определение взаимно простых чисел

Сначала определимся, что значит простое число.

Главное свойство простых чисел в том, что простое число делится только на единицу и на само себя.

• Например, 13 является простым, так как нацело делится только на 1 и на 13.

Таких чисел немного, большинство все-таки можно разделить на другие числа. В простых числах самое важное — это деление нацело. Дробные частные и деление с остатком не рассматриваем.

Понятие взаимно простых чисел можно применить для двух целых чисел или для большего количества. Сформулируем, какие числа называются взаимно простыми.

Взаимно простые числа

Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице — то есть НОД (a, b) = 1.

Проще говоря, взаимно простые числа — это целые числа, у которых нет общих делителей, кроме единицы.

Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать так: НОД (a, b).

Числа, которые содержат больше двух множителей, то есть делятся на несколько чисел, называют сложными . Сложные числа состоят из перемноженных простых.

Наибольший общий делитель взаимно простых чисел — это единица, что следует из определения взаимно простых чисел.

Из определения взаимно простых чисел можно сделать вывод, что у двух взаимно простых чисел может быть только один положительный общий делитель, который равен единице. А всего общих делителей у двух взаимно простых чисел два — это 1 и -1.

Приведем примеры взаимно простых чисел.

• Числа 13 и 16 взаимно простые потому, что их положительный общий делитель — единица, что подтверждает взаимную простоту чисел 13 и 16.

Заметим, что два простых числа всегда являются взаимно простыми. Однако, два числа не обязательно должны быть простыми, чтобы быть взаимно простыми. Вот такая математика в 5 классе. И еще раз: либо одно из них, либо они оба могут быть составными и при этом являться взаимно простыми. Приведем пример.

• Два составных числа 8 и -9 являются взаимно простыми. Как доказать что числа взаимно простые? Объясним:

Сначала найдем НОД этих чисел, то есть запишем все делители чисел 8 и -9.

Делители 8: ±1, ±2, ±4, ±8.

Делители -9: ±1, ±3, ±9.

Из этого следует, НОД (8, -9) = 1, поэтому, по определению 8 и -9 — два взаимно простых числа.

• А вот числа 45 и 500 нельзя назвать взаимно простыми, так как у них есть положительный общий делитель, отличный от единицы — это число 5. Числа 3 и -201 тоже не взаимно простые, так как у них общий положительный делитель — тройка.

На математике в 5 и 6 класса часто встречаются задания, в которых нужно доказать, что конкретные целые числа являются взаимно простыми. Из чего обычно состоит такое доказательство:

• вычисление наибольшего общего делителя заданных чисел,
• проверка НОД на его равенство единице.

Перед вычислением НОД можно заглянуть в таблицу простых чисел и проверить, вдруг исходные целые числа можно назвать простыми. Тогда решение будет проще, так как мы знаем, что НОД простых чисел равен единице.

Повторим еще раз. Что значит взаимно простые числа? Это целые числа, у которых нет общих делителей, кроме единицы.

Пример 1

Доказать, что числа 84 и 275 являются взаимно простыми.

Сверяемся с таблицей простых чисел. 84 и 275 не являются простыми, поэтому нельзя сразу сказать об их взаимной простоте.

Вычислим НОД. Используем алгоритм Евклида для нахождения НОД:

Доказали, что числа 84 и 275 взаимно простые.

Определение взаимно простых чисел можно расширить для трех и большего количества чисел.

Целые числа a ₁ , a ₂ ,…, a _k , где k > 2 называются взаимно простыми , если наибольший общий делитель этих чисел равен единице.

То есть если у некоторого набора целых чисел есть положительный общий делитель, отличный от единицы, то эти целые числа не являются взаимно простыми.

Любая совокупность простых чисел составляет набор взаимно простых чисел, например, 2, 3, 11, 19, 151, 293 и 677 — взаимно простые числа. А четыре числа 12, −9, 900 и −72 не являются взаимно простыми, так как у них есть положительный общий делитель 3. Числа 17, 85 и 187 тоже не взаимно простые, потому что каждое из них можно разделить на 17.

Как определить взаимно простые числа:

• найти наибольший общий делитель этих чисел,
• сделать вывод на основании определения взаимно простых чисел.

Пример 2

Являются ли числа 331, 463 и 733 взаимно простыми?

Заглянем в таблицу простых чисел. Видим, что 331, 463 и 733 — простые. Значит, у них есть единственный положительный общий делитель — единица. Поэтому, 331, 463 и 733 есть взаимно простые числа.

Пример 3

Доказать, что числа −14, 105, −2 107 и −91 не являются взаимно простыми.

Найдем НОД заданных чисел и убедимся, что он не равен единице.

Делители целых отрицательных чисел совпадают с делителями соответствующих противоположных чисел. Поэтому НОД (−14, 105, 2 107, −91) = НОД (14, 105, 2 107, 91). Посчитаем:

НОД (14, 105, 2 107, 91) = 7.

Мы получили, что наибольший общий делитель исходных чисел равен семи, поэтому эти числа не являются взаимно простыми. Доказали.

Свойства взаимно простых чисел

У взаимно простых чисел есть определенные свойства. Рассмотрим основные свойства взаимно простых чисел.

Свойство 1

Числа, которые получились при делении целых чисел a и b на их наибольший общий делитель, называются взаимно простыми. То есть, a : НОД (a, b) и b : НОД (a, b) — взаимно простые.

Это свойство взаимно простых чисел помогает находить пары взаимно простых чисел. Для этого достаточно взять два любых целых числа и разделить их на наибольший общий делитель. В результате получим взаимно простые числа.

Свойство 2

Необходимое и достаточное условие взаимной простоты чисел a и b — это наличие таких целых чисел u₀ и v₀ , при которых будет верным равенство au₀ + bv₀ = 1.

Докажем эту необходимость:

Пусть числа a и b взаимно простые. Тогда по определению взаимно простых чисел НОД (a, b) = 1. А из свойств НОД мы знаем, что для целых чисел a и b верно соотношение Безу au₀ + bv₀ = НОД (a, b). Следовательно, au₀ + bv₀ = 1.

Соотношение Безу — представление НОД целых чисел в виде их линейной комбинации с целыми коэффициентами.

Докажем достаточность:

Пусть верно равенство au₀ + bv₀ = 1. Так как НОД (a, b) делит и a и b, то НОД (a, b) в рамках свойств делимости может делить сумму au₀ + bv₀ , а значит, и единицу. А это возможно только когда НОД (a, b) = 1. Следовательно, a и b — взаимно простые числа.

Свойство 3

Если числа a и b взаимно простые, и произведение ac делится на b — значит c делится на b.

Действительно, так как a и b взаимно простые, то из предыдущего свойства у нас есть равенство au₀ + bv₀ = 1. Если умножть обе части этого равенства на c, получится acu₀ + bcv₀ = c.

Первое слагаемое суммы acu₀ + bcv₀ делится на b, так как ac делится на b по условию, второе слагаемое этой суммы также делится на b, так как один из множителей равен b. Можно сделать вывод, что вся сумма делится на b. А так как сумма acu₀ + bcv₀ равна c, то и c делится на b.

Свойство 4

Если числа a и b взаимно простые, то НОД (ac, b) = НОД (c, b).

Покажем, во-первых, что НОД (ac, b) делит НОД (c, b), а во-вторых, что НОД (c, b) делит НОД (ac, b), это и будет доказывать равенство НОД (ac, b) = НОД (c, b).

НОД (ac, b) делит и ac и b, а так как НОД (ac, b) делит b, то он также делит и bc. То есть, НОД (ac, b) делит и ac и bc, следовательно, в силу свойств наибольшего общего делителя он делит и НОД (ac, bc), который по свойствам НОД равен c * НОД (a, b) = c. Таким образом, НОД (ac, b) делит и b и c, следовательно, делит и НОД (c, b).

С другой стороны, НОД (c, b) делит и c и b, а так как он делит с, то также делит и ac. Поэтому НОД (c, b) делит и ac и b, следовательно, делит и НОД (ac, b).

Так мы показали, что НОД (ac, b) и НОД (c, b) взаимно делят друг друга, значит, они равны.

Свойство 5

Если числа из последовательности a₁ , a₂ , …, a_k будут взаимно простыми с каждым из чисел b₁ , b₂, …, b_m (где k и m — некоторые натуральные числа), то произведения a₁ * a₂ *…*a_k и b₁ *b₂ *…*b_m есть взаимно простые. В частности, если a₁ = a₂ =…= a_k = a и b₁ = b₂ =…= b_m = b, то a_k и b_m — взаимно простые числа.

Предыдущее свойство взаимно простых чисел поможет намзаписать ряд равенств вида:

НОД (a₁ *a₂ *…*a_k , b_m ) = НОД (a₂ *…*a_k , b_m ) =…= НОД (a_k , b_m ) = 1, где последний переход возможен, так как a_k и b_m взаимно простые по условию.

Так мы получили равенство НОД (b₁ *b₂ *…*b_m , a₁ *a₂ *…*a_k ) = 1, которое доказывает, что произведения a₁ *a₂ *…*a_k и b₁ *b₂ *…*b_m являются взаимно простыми.

Определение попарно простых чисел

Через взаимно простые числа можно дадим определение попарно простых чисел.

Попарно простые числа — это последовательность целых чисел a ₁ , a ₂ , …, a _k , где каждое число будет взаимно простым по отношению к остальным.

Приведем пример попарно простых чисел.

• 14, 9, 17, и −25 — попарно простые, так как пары чисел 14 и 9, 14 и 17, 14 и −25, 9 и 17, 9 и −25, 17 и −25 представляют из себя взаимно простые числа.

При этом, взаимно простые числа далеко не всегда могут быть попарно простыми. Подтвердим на примере. 8, 16, 5 и 15 не являются попарно простыми, так как числа 8 и 16 не взаимно простые. Однако, 8, 16, 5 и 15 — взаимно простые. Таким образом, 8, 16, 5 и 15 — взаимно простые, но не попарно простые.

Остановимся на понятии совокупности некоторого количества простых чисел. Эти числа всегда являются и взаимно простыми и попарно простыми. Например, 71, 443, 857, 991 — и попарно простые, и взаимно простые.

Когда речь идет о двух целых числах, то для них понятия «попарно простые» и «взаимно простые» совпадают.

Источник

Разложение чисел на простые множители, способы и примеры разложения

Данная статья дает ответы на вопрос о разложении числа на простыне множители. Рассмотрим общее представление о разложении с примерами. Разберем каноническую форму разложения и его алгоритм. Будут рассмотрены все альтернативные способы при помощи использования признаков делимости и таблицы умножения.

Что значит разложить число на простые множители?

Разберем понятие простые множители. Известно, что каждый простой множитель – это простое число. В произведении вида 2 · 7 · 7 · 23 имеем, что у нас 4 простых множителя в виде 2 , 7 , 7 , 23 .

Разложение на множители предполагает его представление в виде произведений простых. Если нужно произвести разложение числа 30 , тогда получим 2 , 3 , 5 . Запись примет вид 30 = 2 · 3 · 5 . Не исключено, что множители могут повторяться. Такое число как 144 имеет 144 = 2 · 2 · 2 · 2 · 3 · 3 .

Не все числа предрасположены к разложению. Числа, которые больше 1 и являются целыми можно разложить на множители. Простые числа при разложении делятся только на 1 и на самого себя, поэтому невозможно представить эти числа в виде произведения.

При z , относящемуся к целым числам, представляется в виде произведения а и b , где z делится на а и на b . Составные числа раскладывают на простые множители при помощи основной теоремы арифметики. Если число больше 1 , то его разложение на множители p 1 , p 2 , … , p n принимает вид a = p 1 , p 2 , … , p n _. Разложение предполагается в единственном варианте.

Каноническое разложение числа на простые множители

При разложении множители могут повторяться. Их запись выполняется компактно при помощи степени. Если при разложении числа а имеем множитель p 1 , который встречается s 1 раз и так далее p n – s n раз. Таким образом разложение примет вид a=p₁ s ₁· a = p 1 s 1 · p 2 s 2 · … · p n s n . Эта запись имеет название канонического разложения числа на простые множители.

При разложении числа 609840 получим, что 609 840 = 2 · 2 · 2 · 2 · 3 · 3 · 5 · 7 · 11 · 11 ,его канонический вид будет 609 840 = 2 4 · 3 2 · 5 · 7 · 11 2 . При помощи канонического разложения можно найти все делители числа и их количество.

Алгоритм разложения числа на простые множители

Чтобы правильно разложить на множители необходимо иметь представление о простых и составных числах. Смысл заключается в том, чтобы получить последовательное количество делителей вида p 1 , p 2 , … , p n чисел a , a 1 , a 2 , … , a n — 1 , это дает возможность получить a = p 1 · a 1 , где a 1 = a : p 1 , a = p 1 · a 1 = p 1 · p 2 · a 2 , где a 2 = a 1 : p 2 , … , a = p 1 · p 2 · … · p n · a n , где a n = a n — 1 : p n . При получении a n = 1 , то равенство a = p 1 · p 2 · … · p n получим искомое разложение числа а на простые множители. Заметим, что p 1 ≤ p 2 ≤ p 3 ≤ … ≤ p n .

Для нахождения наименьших общих делителей необходимо использовать таблицу простых чисел. Это выполняется на примере нахождения наименьшего простого делителя числа z . При взятии простых чисел 2 , 3 , 5 , 11 и так далее, причем на них делим число z . Так как z не является простым числом, следует учитывать, что наименьшим простым делителем не будет больше z . Видно, что не существуют делителей z , тогда понятно, что z является простым числом.

Рассмотрим на примере числа 87 . При его делении на 2 имеем, что 87 : 2 = 43 с остатком равным 1 . Отсюда следует, что 2 делителем не может являться, деление должно производиться нацело. При делении на 3 получим, что 87 : 3 = 29 . Отсюда вывод – 3 является наименьшим простым делителем числа 87 .

При разложении на простые множители необходимо пользоваться таблицей простых чисел, где a . При разложении 95 следует использовать около 10 простых чисел, а при 846653 около 1000 .

Рассмотрим алгоритм разложения на простые множители:

• нахождение наименьшего множителя при делителе p 1 числа a по формуле a 1 = a : p 1 , когда a 1 = 1 , тогда а является простым числом и включено в разложение на множители, когда не равняется 1 , тогда a = p 1 · a 1 и следуем к пункту, находящемуся ниже;
• нахождение простого делителя p 2 числа a 1 при помощи последовательного перебора простых чисел, используя a 2 = a 1 : p 2 _,когда a 2 = 1 , тогда разложение примет вид a = p 1 · p 2 _,когда a 2 = 1 , тогда a = p 1 · p 2 · a 2 _, причем производим переход к следующему шагу;
• перебор простых чисел и нахождение простого делителя p 3 числа a 2 по формуле a 3 = a 2 : p 3 , когда a 3 = 1 , тогда получим, что a = p 1 · p 2 · p 3 _, когда не равняется 1 , тогда a = p 1 · p 2 · p 3 · a 3 и производим переход к следующему шагу;
• производится нахождение простого делителя p n числа a n — 1 при помощи перебора простых чисел с p n — 1 , а также a n = a n — 1 : p n , где a n = 1 , шаг является завершающим, в итоге получаем, что a = p 1 · p 2 · … · p n _.

Результат алгоритма записывается в виде таблицы с разложенными множителями с вертикальной чертой последовательно в столбик. Рассмотрим рисунок, приведенный ниже.

Полученный алгоритм можно применять при помощи разложения чисел на простые множители.

Примеры разложения на простые множители

Во время разложения на простые множители следует придерживаться основного алгоритма.

Источник