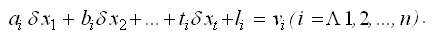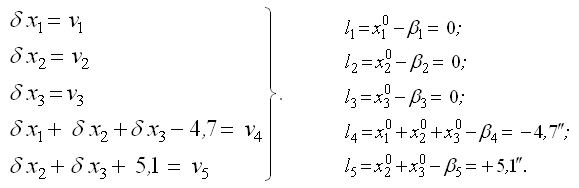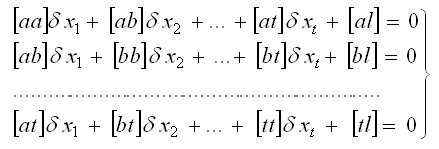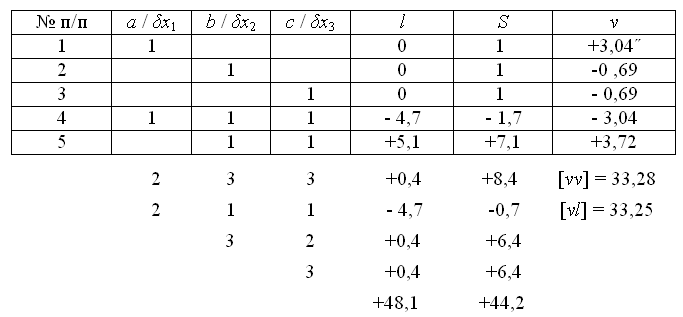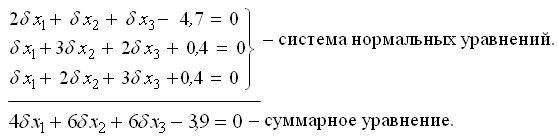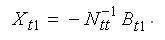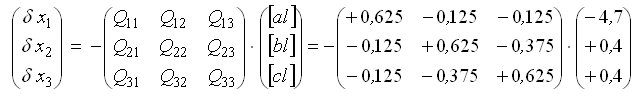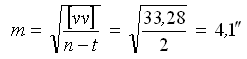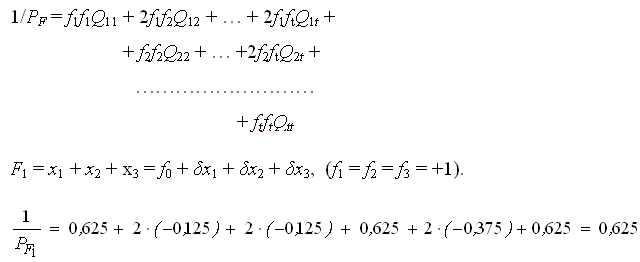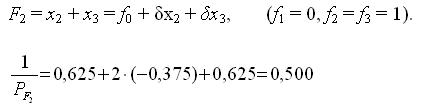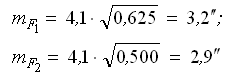Сущность параметрического способа уравнивания
При уравнивании геодезических сетей параметрическим способом первоначально выбираются так называемые параметры, через которые посредством уравнений связи выражается каждая измеренная величина. Поэтому непосредственно уравниваемыми величинами являются параметры, а затем уже по уравненным значениям параметров вычисляются уравненные значения непосредственно измеренных величин..
Пусть в геодезической сети измерено 













где 



Уравнения (7.43) называются параметрическими уравнениями связи в общем виде .
Как уже ранее отмечалось, целью уравнительных вычислений является вычисление таких поправок 



уравненные значения измеренных величин, а через

уравненные значения параметров, где 






1. Гудков В.М., Хлебников А.В. Математическая обработка маркшейдерско-геодезических измерений. Учеб. для вузов. – М.: Недра, 1990.– 335 с.
2. Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений. – М.: Недра, 1977. 387 с.
3. Смолич Б.А. Уравнительные вычисления. Учеб. для техникумов – М.: Недра, 1989. – 245 с.
4. Мазмишвили А.И. Теория ошибок и метод наименьших квадратов. – М.: Недра, 1978. 311 с.
5. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учеб. для втузов. Т.1 – М.: Недра, 1970. 456с.
6. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учеб. для втузов. Т.2 – М.: Недра, 1970. 576с.
7. Бермант А.Ф. Курс математического анализа. Часть 1. – М.: Госуд. изд-во физ-мат. литературы. 1959, 466 с.
8. Селиханович В.Г. Геодезия. Учеб. для вузов.Ч. II – М.: Недра, 1981. 544 с.
Источник
Вывод алгоритма уравнивания параметрическим способом
Необходимо найти такой вектор х , чтобы он был несмещ-ой, дост-ой и эффект-ой оценкой. Поскольку вектор х есть вектор поправок в приближенные значения координат , то и корд-ты будут несмещ-мии эффек-ми, т.е. наиболее точными. Вывод алгоритма уравнивания будем вести на основе оценки функции уравненных значений параметров х и измерен.l . Суть вывода алгоритма заключ. В том, что некоторую 
Пусть им-ся упавнения значений отметок 1,2. , то превышение как функции h=Z=H2-H1. С другой стороны этот же результат мы должны пол-ть выраж. Z=-b1*l1-b2*l2-b3*l3, где l1, l2, l3-свободн. Члены уравнения поправок для измер. превыш. h1,h2,h3. l1=H 0 1-HA-h1; l2=H 0 2-H 0 1-h2; l3=HB-H 0 2-h3, где HA,Hb – высоты исходных реперов А и В, H 0 i-приближ. значения высот опред. реперы 1 и 2.В данном случае С T =(-1 +1), X = H1 Задача заключ. в том , чтобы найти такой вектор B T , чтобы
оценка функции Z была достаточной. несмещ. и эффективной. Решение задачи в общем виде: Z= C T X, Z=-b T L, V=AX+L(урав-е поправок). 1. достат-ть: Дост-ть оц. фуккции Z в каком бы виде она не была зап. измер. налич. обр-ки всех измерений, т.е. всей системы уравнений поправок.2. несмещ-ть. Очевидно, что матем. ожидание Z : MZ = C T МX, MZ =-b T МL. Согласно условию несмещ-ти мат. ожидание вектора поправок д.б.=0, тогда будет след. выражение: MV=AМX+МL, Поск-ку MV=0, то
AМX= — МL. Введем алгебр. запись условия несмещ-ти для этого полагаем, что МL= -AМX, MZ= C T МX, MZ= -b T (-AМX) левые части этих выражений = MZ, то C T МX =b T (-AМX); C T = b T A или A T b=C. Чтобы оценка была несмещенной должно вып-ся это условие. 3. Эффектив-ть. Согласно этому свойству или условию дисперсия функции Z д.б. минимальной. Z=-b T L DZ=b T KLb=min. Min дисперсия будет наход-ся при условии несмещенности: DZ= b T KLb+2λ Т (A T b-С) =min. Поск-ку свобод. Член выч-ся по измер., то это есть корреляционная матрица измерений KL= σ 2 * P -1 (σ =стандарт вес которогопринят =1, Р- весовая матрица). Найдем вектор b в этой задаче. DZ= σ 2 b T P -1 b+2λ Т (A T b-С) =min; ∂ DZ /∂b=2 σ 2 b T P -1 +2λ Т A T =0; σ 2 b T P -1 +λ Т A T =0; σ 2 b T P -1 =- λ Т A T
Для решения этого уравнения умножим его справа на матрицу Р: σ 2 b T P -1 Р = — λ Т A T Р, σ 2 b T = — λ Т A T Р, b T = — λ Т A T Р1/ σ 2 . В этом выраж. неиз-м яв-ся λ Т . Найдем его из условия несмещ-ти. b T A- C T = 0. Подст-м это условие в b T : -1/ σ 2 λ Т A T РA- C T = 0; -1/ σ 2 λ Т N- C T = 0; -λ Т N= σ 2 C T . Для вычисления λ Т умножим это выражение на N -1 : -λ Т N N -1 = σ 2 C T N -1 , -λ Т = σ 2 C T N -1 , λ Т = -σ 2 C T N -1 . Ранее было b T =1/ σ 2 λ Т A T Р. Подст-м λ Т : b T = C T N -1 A T Р. Поск-ку мы ранее иск. Z= -C T N -1 A T РL
В частном случае, если Z=X, C T =Е, тогда X= -N -1 A T РL- это единичная несмещ, эффективн. оценка поправок в приближенные значения координат, а значит и координ-т опред-х пунктов DZ= b T KLb, KL= σ 2 * P -1 , b T = C T N -1 A T Р, DZ= C T N -1 A T Р* σ 2 * P -1 РA N -1C , Р* P -1 =Е, , DZ= σ 2 C T
N -1 A T Р A N -1C, AT Р A=N, тогда DZ= σ 2 C T N -1 N N -1C, N N -1 =Е, DZ= σ 2 C T N -1 C. В частном случае C T =Е , тогда DZ=DX= σ 2 N -1
Таким образом, алгоритм уравнивания параметрическим способом заключается в следующем:
а) составляется система уравнений поправок V=A*X+L
б) вычисляется матрица нормальных уравнений N = А T РА;
в) находится вектор параметров X=-N -1 A T РLи оценивается его точность DX= σ 2 N -1
Настоящий алгоритм можно вывести и на основе метода наименьших квадратов. Согласно этому методу должно выполняться условие: V T PV=min, V=AX+L. Неиз-н вектор Х? Ф= V T PV, ∂ Ф/∂х=2V T P∂ V/∂х=0, V=AX+L, ∂ V/∂x=A, ∂ Ф/∂х=2V T PA=0, V T PA=0, (V T PA) T =0, A T PV=0, A T P(AX+L)=0, A T PA+ A T PL=0, A T PA=N, Nx+ A T PL=0, Nx=- A T PL. Для вычисления умножим эту матрицу на N -1 слева. N -1 Nx=- N -1 A T PL, x=- N -1 A T PL
Источник
Уравнивание углов на станции параметрическим способом
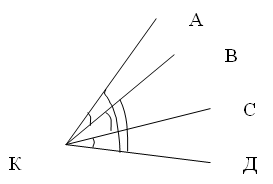
В табл. 13 даны результаты равноточных измерений углов на станции (рис. 4).
Рис. 4. Углы на станции
Результаты измерений βi
| № углов | Углы | βi | № углов | Углы | βi |
| АКВ | 20° 00′ 05,2″ | АКД | 65° 20′20,0″ | ||
| ВКС | 20° 00′ 10,1″ | ВКД | 45° 20′ 05,0″ | ||
| СКД | 25° 20′ 00,0″ |
Число всех измеренных углов n = 5; число необходимых измерений t = 3.
Выберем в качестве параметров х1, х2, х3 соответственно первый, второй, третий углы. Четвертый и пятый углы можно представить как суммы параметров.
Составим параметрические уравнения связи по формуле:
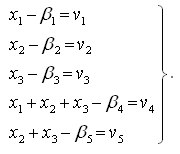
Введем приближенные значения параметров, приняв их равными измеренным значениям соответствующих углов:
Перейдем к параметрическим уравнениям поправок:
Составим нормальные уравнения:
Bычислим коэффициенты и свободные члены нормальных уравнений (табл. 14).
Таблица параметрических уравнений
Систему нормальных уравнений решим методом обращения
Элементы обратной матрицы Ntt -1 получим на ПК, используя математические функции электронных таблиц Еxсel или системы Mathсad.
Контроль вычисления неизвестных:
4·3,038 +6·(-0,688) + 6·(-0,688) — 3,9 = 0.
В табл. 14 по формуле (28) вычислим поправки к результатам измерений. Сделаем контроль решения по МНК.
Найдем уравненные значения углов 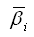
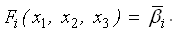
Оценим точность результатов измерений.
— средняя квадратическая ошибка результатов измерений.
Уравненные значения углов. Контроль уравнивания
| № п/п | 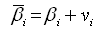 | Параметры и их функции | Fi(x1, x2, x3) |
| 20°00′ 08,24″ | x1 | 20° 00′ 08,24″ | |
| 20° 00′ 09,41″ | x2 | 20° 00′ 09,41″ | |
| 25° 19′ 59,31″ | x3 | 25° 19′ 59,31″ | |
| 65° 20′ 16,96″ | x1 + x2 +x3 | 65° 20′ 16,96″ | |
| 45° 20′ 08,72″ | x2 + x3 | 45° 20′ 08,72″ |
Оценим точность уравненных углов. Обратный вес функции найдем через элементы обратной матрицы по формуле:
— обратный вес первой функции.
— обратный вес второй функции.
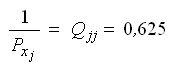
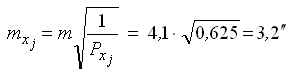
— средние квадратические ошибки весовых функций.
Источник