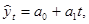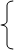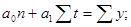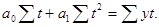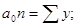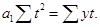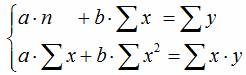Выравнивание рядов динамики



При исследовании рядов динамики одной из важнейших задач является определение основной тенденции развития явления (тренда) и сглаживание случайных колебаний. С этой целью используются следующие методы выравнивания рядов динамики:
1)метод укрупнения интервалов;
2)метод скользящей средней;
3) аналитическое выравнивание рядов динамики.
Метод укрупнения интервалов основан на том, что первоначальный ряд динамики заменяется другим, уровни которого относятся к большим по продолжительности периодам времени. Средние, исчисленные по укрупненным интервалам, позволяют выявлять направление и характер основной тенденции развития.
Суть метода скользящей средней заключается в том, что для первоначального ряда динамики формируются увеличенные интервалы, состоящие из одинакового количества уровней. Каждый последующий интервал получается смещением от начального на один уровень. В каждом укрупненном интервале скольжения рассчитывается средний уровень, который относится к середине этого интервала. В результате этого получается новый ряд из скользящих средних, позволяющий выявить тенденцию развития явления.
Смысл метода аналитического выравнивания состоит в замене фактических уровней ряда динамики сглаженными, рассчитанными по соответствующей математической функции.
Рассмотрим сущность данного метода на примере выравнивания по прямой.
Уравнение прямой имеет следующий вид:
где 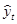
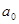
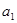
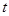
Параметры 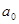
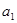
Расчет параметров прямой можно упростить, если отсчет времени 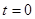
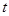
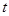
При условии, что 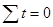
Откуда 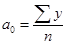
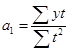
Аналитическое выравнивание может быть использовано при прогнозировании статистических показателей путем экстраполяции, т. е. нахождения уровней за пределами данного ряда динамики.
Источник
Метод аналитического выравнивания
Назначение сервиса . Сервис позволит прямо на сайте в онлайн-режиме провести аналитическое выравнивание ряда yt, проверить наличие гетероскедастичности и автокорреляции остатков тестом Дарбина-Уотсона (см. пример аналитического выравнивания по прямой).
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Чтобы привести нелинейные зависимости к линейной используют метод выравнивания (линеаризацию).
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
В общем случае при аналитическом выравнивании используется метод наименьших квадратов:
- Система нормальных уравнений для линейной зависимости:
- Система нормальных уравнений для полинома второй степени (параболы):
- Система нормальных уравнений для полинома третьей степени:
Типичное задание. Произведите аналитическое выравнивание и выразите общую тенденцию развития розничного товарооборота торгового дома соответствующим аналитическим уравнением. Вычислите аналитические (выровненные) уровни ряда динамики и нанесите их на график вместе с фактическими данными.
Пример . По УР имеются данные о вводе в действие жилых домов и общежитий, тыс. м 2 . Для анализа динамики показателя ввода в действие жилых домов и общежитий вычислите:
- абсолютные приросты, темпы роста и темпы прироста по годам и к 1998 г., абсолютное содержание одного процента прироста. Полученные показатели представьте в виде таблицы;
- среднегодовые показатели — величину уровня ряда; абсолютный прирост темп роста и прироста. Сделайте выводы.
Постройте график динамики уровня ряда за период 1998 -2006 гг., проведите аналитическое выравнивание ряда (постройте математическую модель и график), сделайте прогноз на 2007 год.
Источник
Ряды динамики в статистике
9.3. Методы анализа основной тенденции в рядах динамики
Комплексный анализ динамических рядов, как правило, включает не только расчет характеристик интенсивности изменения уровней ряда при переходе от одного момента или промежутка времени к другому (абсолютных приростов, коэффициентов и темпов роста и прироста), а также нахождение обобщенных средних характеристик (среднего уровня ряда, средних темпов роста и прироста), но и выявление основных закономерностей в развитии динамического ряда. Определение тенденции развития, построение модели, описывающей изменение явления во времени, прогнозирование явления — все это важнейшие задачи при изучении динамических рядов экономических и социальных показателей.
На формирование уровней динамического ряда влияет множество различных факторов, которые по характеру воздействия можно объединить в три группы:
- действующие долговременно и определяющие основную тенденцию развития явления;
- действующие периодически — сезонные и циклические колебания;
- вызывающие случайные колебания уровней динамического ряда.
Соответственно, для анализа закономерности изменения уровней ряда динамики во времени применяют следующую модель:
где Тt — основная тенденция ряда ( тренд );
St — циклические (в частности, сезонные) колебания;
еt — случайные колебания.
В аддитивной модели ряд динамики представлен как сумма перечисленных компонент [yt = Tt + St + et], в мультипликативной модели — как их произведение [
Тенденцией развития, или трендом, называется сформировавшееся направление развития явления во времени под воздействием постоянно действующих факторов. Судить о наличии тенденции в динамическом ряду на основе его визуального анализа можно лишь тогда, когда четко видно, что при переходе от одного момента времени к другому уровни ряда возрастают или убывают. Однако, как правило, нельзя сразу сказать, есть или нет тенденция в изменении уровней динамического ряда. Для этого применяются специальные методы.
К методам выявления основной тенденции развития динамического ряда (Тt) относятся:
- метод укрупнения интервалов;
- метод скользящей средней;
- аналитическое выравнивание динамических рядов.
Рассмотрим их подробнее.
9.3.1. Метод укрупнения интервалов
Применение метода укрупнения интервалов рассмотрим на основе данных табл. 9.13.
| Месяц | Поставка товаров, млн руб. |
|---|---|
| Январь | 80 |
| Февраль | 78 |
| Март | 75 |
| Апрель | 80 |
| Май | 82 |
| Июнь | 85 |
| Июль | 87 |
| Август | 82 |
| Сентябрь | 85 |
| Октябрь | 84 |
| Ноябрь | 86 |
| Декабрь | 88 |
Как видим, визуальный анализ данных не позволяет сделать какие-либо выводы о наличии тенденции в данном динамическом ряду: в отдельные месяцы, например, в феврале, марте, августе, октябре и декабре, поставки товаров снижались по сравнению с предыдущими месяцами, в остальные периоды — возрастали.
Применим к исходным данным метод укрупнения интервалов, образовав новый динамический ряд с более крупными временными периодами — кварталами, и рассчитаем средний месячный объем поставок в каждом квартале (табл. 9.14).
| Квартал | Среднемесячные поставки товаров, млн руб. |
|---|---|
| I | 77.7 |
| II | 82.3 |
| III | 84.0 |
| IV | 84.7 |
Итак, по новым, более крупным интервалам уже четко видно, что значения исследуемого признака во временном аспекте имеют тенденцию к возрастанию.
Применение рассмотренного метода в основном ограничивается теми ситуациями, когда исходные данные относятся к дням, неделям или месяцам года, так как значения исследуемого признака по более мелким временным интервалам больше подвержены случайным колебаниям. Если временные промежутки представляют собой годы, то укрупнение интервалов становится малоэффективным.
9.3.2. Метод скользящей средней
Следующий способ выявления тенденции в динамическом ряду основан на расчете и анализе так называемых скользящих (подвижных) средних.
Скользящими (подвижными) средними называются средние арифметические значения показателя, исчисленные по новым m-членным укрупненным интервалам. Правила построения этих интервалов следующие. Первый из интервалов включает первые m уровней ряда динамики, второй интервал образуется путем исключения первого члена укрупненного интервала и замены его последующим элементом ряда динамики, имеющим номер (m + 1) и т.д. — до включения в интервал последнего уровня ряда. По вычисленным подобным путем подвижным средним делают вывод о существовании тенденции в динамическом ряду.
Если в качестве укрупненного интервала используют период в три месяца, то первая подвижная трехчленная средняя вычисляется как средняя арифметическая из данных за январь, февраль и март, вторая — как средняя арифметическая из данных за февраль, март, апрель и т.д. Значения подвижных средних относят к конкретному временному периоду, соответствующему середине укрупненного интервала.
Проведем сглаживание ряда методом скользящей средней по трем членам (табл. 9.15).
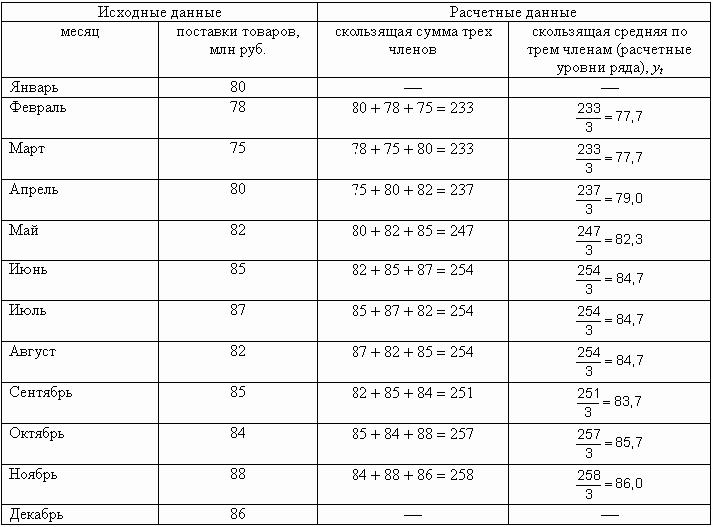 |
В нашем примере первая скользящая средняя относится к февралю, вторая — к марту и т. д.
В тех случаях, когда сглаживание проводится по четному числу уровней ряда динамики, середина временного интервала сглаживания будет находиться между двумя моментами (периодами) времени. Например, если проводить сглаживание по четырем членам, середина первого интервала будет находиться между февралем и мартом, второго интервала — между мартом и апрелем и т.д. В таких случаях возникает необходимость центрирования полученных результатов для отнесения сглаженных значений показателя к конкретным периодам или моментам времени. Расчет центрированных скользящих средних может проводиться в два этапа:
- определение скользящих сумм и нецентрированных скользящих средних по четному числу уровней ряда динамики;
- исчисление центрированных скользящих средних из двух смежных ранее исчисленных нецентрированных скользящих средних и отнесение их к соответствующим периодам или моментам времени.
Методика расчета центрированных скользящих средних показана ниже (табл. 9.16).
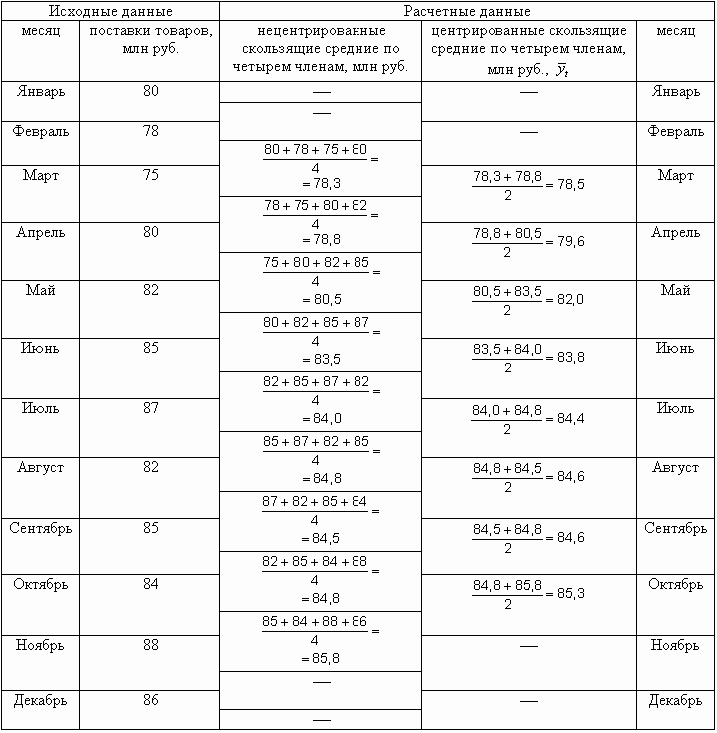 |
9.3.3. Аналитическое сглаживание (выравнивание) рядов динамики
Аналитическое выравнивание динамических рядов — это нахождение определенной модели (уравнения тренда), которая математически описывает тенденцию развития явления во времени. При этом уровни показателя рассматриваются только как функция от времени. В отличие от рассмотренных выше методов, таких, как укрупнение интервалов, скользящих средних, направленных в основном на то, чтобы ответить на вопрос: есть ли тенденция в динамическом ряду или нет, и определить ее направление, аналитическое выравнивание позволяет более точно установить характер развития явления, а главное — описать его математически, уловить все нюансы и направления развития и, что, пожалуй, наиболее интересно, использовать в дальнейшем полученную модель для прогнозирования.
Первым шагом в проведении аналитического выравнивания является выбор вида математической функции, которую предполагается использовать в качестве модели тренда. При этом можно руководствоваться формой кривой, полученной на основе отображения на графике эмпирических данных. Схема построения графика достаточно проста: по оси абсцисс откладываются временные периоды (даты), по оси ординат — значения уровней динамического ряда.
При анализе рядов динамики в качестве линии тренда чаще всего используются следующие функции:
Источник