Выполните умножение чисел способом последовательного поразрядного умножения

Способ последовательного поразрядного умножения

Скачать
презентацию Множимое умножают на круглое число >>

Способ последовательного поразрядного умножения. Этот способ применяется при умножении числа на любое однозначное число. Если нужно умножить двузначное (трех-, четырехзначное и т.д.) число на однозначное, то вначале один из сомножителей умножают на десятки другого сомножителя, потом на его единицы и полученные произведения суммируют. Пример. Найдем произведение чисел 39 и 7. Решение. 39 x 7 = (30 x 7) + (9 x 7) = 210 + 63 = 273.

Слайд 21 из презентации «Рациональный счёт». Размер архива с презентацией 1289 КБ.

Математика 5 класс

«Законы сложения» — Законы арифметических действий. Переместительный закон сложения. Сколько всего игрушек. Сочетательный закон сложения. Справедливы для умножения те же законы, что и для сложения. Маша собрала 11 яблок и 16 груш. 48+ 52. Найдите площадь прямоугольника. Учимся считать быстро. Найдите длину отрезка.

«Математика «Таблица умножения»» — Как пользоваться таблицей умножения. Таблица умножения — достойна уважения. Впервые в школьную программу таблица умножения была введена в Англии. Кто лучше знает таблицу умножения. История создания таблицы умножения. Таблица умножения на 9 на пальцах. Выводы. Для чего нужна таблица умножения. Стихотворения о таблице умножения. Главный вопрос. Цели и задачи.

«Решение дробей с одинаковыми знаменателями» — День. Сложение и вычитание дробей с одинаковыми знаменателями. Закрепление навыков сложения и вычитания дробей. Крестики — нолики. Решение уравнений. Расположите дроби в порядке возрастания. Самостоятельная работа. Логическая задача. Старик. Прогнозируемые результаты. Устный счет. Задачи со сказочным сюжетом.

«Формула площади прямоугольника» — Зачетный лист. Цели урока. Решение задач по теме. Что нужно знать, для того чтобы вычислить площадь. Выполнение упражнений устно. Свойства площадей. Устный счет. Формула площади прямоугольника. Учимся размышлять. Немного из истории. Организационный момент. Какие фигуры называются равными. Площадь.

«5 класс «Измерение углов»» — Пользуясь рисунком, ответить на вопросы. Цель. Определить градусную меру угла. Точка. Найти и вычеркнуть лишний рисунок. Мы на вершине. Оценить сумму градусных мер данных углов. Найти величину угла. Найти и вычеркнуть лишнее слово. Проверь свой глазомер. Найдите на этом рисунке острые, тупые и прямые углы. Виды углов. Исследовательская работа. Сумма трех углов. Определить градусную меру углов по рисунку.

«Задачи на движение» — Навстречу друг другу вышли два пешехода. Догонялки. Движение черепахи. Задачи на движение. Таблица. Два поезда вышли одновременно из одной станции. План урока. Встречное движение. Основные формулы. Из села вышел пешеход. Движение в разные стороны. Задачи урока. Используя формулы пути, скорости и времени найди неизвестную величину. Старинная задача. Математическая модель. Блиц- турнир. Проверь себя и оцени.

Всего в теме «Математика 5 класс» 177 презентаций

Источник

Умники и умницы

Умные дети — счастливые родители

ПНШ 3 класс. Математика. Учебник № 2, с. 17

Умножение на двузначное число

Ответы к с. 17

34. Как выполнить умножение числа 32 на число 23?
Для ответа на этот вопрос можешь воспользоваться следующей цепочкой равенств:
32 • 23 = 32 • (20 + 3) = 32 • 20 + 32 • 3
Какое правило применили в данных преобразованиях? Продолжи вычисления, выполнив умножение устно, а сложение письменно в столбик.

Правило умножения числа на сумму.
32 • (20 + 3) = 32 • 20 + 32 • 3 = 640 + 96
₊640
96
736

35. Рассмотри запись и объясни, как умножили число 412 на двузначное число 21.
412 • 21 = 412 • (20 + 1) = 412 • 20 + 412 • 1 = 8240 + 412 = 8652

Используя правило умножения числа на сумму. Представили число 21 как сумму числа 20 и числа 1, а затем на эту сумму умножили число 412. При этом получилось умножение на «круглое» двузначное число (412 • 20) и умножение на однозначное число (412 • 1).

На какие слагаемые разложили второй множитель? Почему этот способ можно назвать способом поразрядного умножения?

Второй множитель разложили на сумму чисел 20 и 1. При поразрядном умножении умножаются по отдельности разряды, а затем полученное суммируют. Этот способ применяется при умножении одного числа на любое однозначное число. При умножении на число 20 ноль записывается справа к числу 412 и это число умножается на 2.

36. Запиши произведение, значение которого вычислено способом поразрядного умножения в результате последовательного выполнения следующих двух действий умножения и одного действия сложения:
1) 35 • 5 = 175 2) 35 • 20 = 700 3) 175 + 700 = 875

35 • 25 = 35 • (5 + 20) = 35 • 5 + 35 • 20 = 175 + 700 = 875

Источник

Умники и умницы

Умные дети — счастливые родители

ПНШ 3 класс. Математика. Учебник № 2, с. 9

Умножение на однозначное число столбиком

Ответы к с. 9

5. Приведи пример поразрядного умножения четырёхзначного числа на однозначное, при выполнении которого дважды происходит переход через разряд: в разряде единиц и в разряде сотен.

6. Выпиши все трёхзначные числа, при поразрядном умножении которых на число 5 не происходит перехода через разряд.

100, 101, 110, 111. В записи этих чисел используются только цифры 0 и 1. При использовании других цифр, начиная с цифры 2, будет происходить переход через разряд.

7. Выполни умножение столбиком.

8. По данной схеме сформулируй задачу, решить которую можно с помощью двух действий сложения или одного действия сложения и одного действия умножения.
Для вычисления ответа задачи примени умножение столбиком.

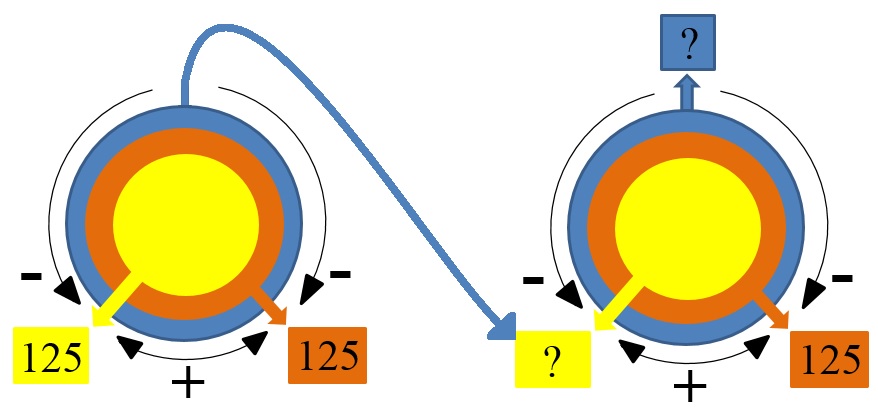
На концерт пришли 125 детей, столько же взрослых и 125 пожилых людей. Сколько всего человек пришло на концерт?
1) _×125
2
250 (ч.) — детей и взрослых
2) 250 + 125 = 375 (ч.) — пришло всего
О т в е т: всего на концерт пришло 375 человек.

Источник

Практическая работа №4 операция умножения чисел в ЭВМ

Практическая работа №4

Операция умножения чисел в ЭВМ

Целью работы является изучение умножения чисел как с фиксированной, так и с плавающей точкой в ЭВМ.

2. Теоретическая часть

2.1. Умножение чисел в двоичной системе счисления.

Наиболее просто умножение выполняется в прямом коде, независимо от того, являются ли операнды целыми или дробными числами. В ЭВМ с фиксированной точкой умножение реализуется в два этапа.

Первый этап заключается в определении знака произведения с помощью сложения знаковых цифр сомножителей по модулю два, где 0 – соответствует плюсу, а 1 – минусу (табл. 2.1.1).

Сложение по модулю два

По-другому, это эквивалентно

На втором этапе производится перемножение модулей сомножителей, затем в случае необходимости округления полученного модуля произведения, после чего к модулю результата приписывается его знак, определенный на первом этапе.

Умножение производится по обычным правилам арифметики, согласно двоичной таблицы умножения (табл. 2.1.2).

Традиционная схема умножения похожа на известную из школьного курса процедуру записи «в столбик». Вычисление произведения двух n-разрядных двоичных чисел без знака сводится к формированию частичных произведений (ЧП) по одному на каждую цифру множителя, с последующим суммированием полученных ЧП. Перед суммированием каждое частичное произведение должно быть сдвинуто на один разряд относительно предыдущего.

2.2. Умножение двоичных чисел в ЭВМ. Машинный метод.

Умножение двоичных чисел сводится к операциям сдвига на один двоичный разряд влево и повторения первого сомножителя в тех разрядах, где второй сомножитель содержит 1, и сдвига без повторения в разрядах с 0. Сдвиг всегда чередуется со сложением, поскольку для выполнения операций имеется всего два регистра (два места для записи чисел). Другими словами, реализации отдельной операции умножения в процессоре не требуется.

Как и в операции сложения, при умножении чисел с ограниченной разрядной сеткой может возникнуть переполнение.

Перемножение двух n-разрядных двоичных чисел P=A*B приводит к получению результата, содержащего 2n битов. Таким образом, алгоритм умножения предполагает последовательное выполнение двух операций – сложения и сдвига. Суммирование ЧП обычно производится не на завершающем этапе, а по мере их получения. Это позволяет избежать необходимости хранения всех ЧП, то есть сокращает аппаратурные издержки. Устройство умножения предполагает наличие регистров множимого, множителя и суммы частичных произведений, а также сумматора ЧП и, возможно, схем сдвига (если операция сдвига не реализована иным способом).

Существуют следующие алгоритмы умножения:

1. Алгоритм сдвига вправо — начиная с младших разрядов множителя, со сдвигом суммы ЧП вправо и при неподвижном множимом.

2. Алгоритм сдвига влево — начиная со старших разрядов множителя, со сдвигом суммы ЧП влево и неподвижном множимом.

Рассмотрим пример умножения двоичных чисел в ЭВМ.

Выполнить умножение чисел A = 101112 и B = 1012 в двоичной системе счисления.

Умножение выполняется в несколько этапов:

1. Впишем множимое A, допустим в 8-ми разрядный регистр, начиная с младших разрядов (нумерация разрядов начинается с нуля). В недостающие разряды записываем нули.

2. Впишем множитель В в 8-ми разрядный регистр, начиная с младших разрядов. В недостающие разряды записываем нули.

3. Подготовим (обнулим) регистр результата C удвоенной разрядности (16 бит). Произведение содержит в два раза больше разрядов чем исходные сомножители.

4. Дальше выполняется следующий цикл:

4.1. Анализируем очередной разряд множителя В (начинаем с младших), если он «1», то прибавляем множимое A к старшим разрядам регистра С, результат снова в С. Если очередной разряд множителя «0», пропускаем данный шаг.
4.2. Сдвигаем содержимое регистра С на один разряд вправо. При этом крайний левый (старший) разряд заполняется нулем. Но если перед этим была операция сложения, во время которой возник перенос из старшего разряда, то тогда крайний левый разряд заполняется единицей.

4.3. Действия, описанные в п. п. 5.1 и 5.2,повторяютсядо тех пор не будут проанализированы все разряды множителя.

В итоге процесс умножения выглядит следующим образом:

где «+А» — числоА прибавляется к регистру C; «—>»содержимое регистра C сдвигается на один разряд вправо; «=» — показывается значение частичного произведения полученного после сложения, которое заносится в регистр С.

5. Определяется знак результата. Если знаки исходных сомножителей одинаковы, то результирующее произведение положительно и наоборот. В данном случае знаки совпадают, следовательно результирующее произведение положительно.

В итоге получается ответ:

Выполнить умножений и деление чисел согласно варианту задания.

4.1. Выполнить умножение чисел A и B в двоичной системе счисления, используя ручной метод. Показать решение.

4.2. Выполнить умножение чисел A и B двоичной системе счисления, используя машинный метод. Разрядность регистров выбрать самостоятельно. Показать решение.

Источник

Конспект урока. Тема урока № 76: «Умножение на двузначное число»

1. Тема урока № 76: «Умножение на двузначное число»

2. Предмет — математика

4. Автор разработок – , учитель начальных классов

5. МОУ «Сорочинская СОШ»

6. Калачинский район

7. Краткое описание: разработаны два урока№76, 77 использована технология деятельностного подхода.

8. Тип урока — изучение нового материала

9. Форма организации — урок

10. Представление о результатах:

Личностные результаты – сформировать ценностные отношения к самостоятельному нахождению способа решения проблемной ситуации.

Метапредметные результаты – уметь ставить цель, обсуждать, доказывать свое мнение, делать вывод.

Предметные результаты — уметь умножать многозначное число на двузначное число способом поразрядного умножения.

-формировать умение выполнять умножение на двузначное число, используя правило умножения числа на сумму;

— совершенствовать вычислительные навыки;

— закреплять умение формулировать задачу по схеме;

-развивать умение рассуждать, анализировать, делать выводы;

— повышать интерес к учебе.

Организация рабочего места и эмоциональный настрой

-Здравствуйте, ребята. (Слайд 2)

-Встало солнышко давно,
Заглянуло к нам в окно.

Нас оно торопит в класс,
Математика у нас!

-Проверьте свое рабочее место. Все ли готово к уроку?

Откинули лень. Настроились на хорошую работу.

Дети проверяют, всё ли приготовили к уроку на столе.

Настраиваются на работу.

Самооценка готовности к уроку.

Повторить необходимые и достаточные знания табличных случаев умножения и правила умножения двузначного числа на однозначное. Создать проблемную ситуацию.

А) Найди лишнее число в каждом столбике: (Слайд 3)

Б) Поставь знаки, чтобы получилось верное равенство: (Слайд 4)

В) Поставь числа, чтобы получились верные равенства (несколько вариантов: ответа) (Слайд 5)

Г) Найди значения выражений: (Слайд 6)

— С какой трудностью столкнулись?

Дети выполняют задания учителя.

Предъявляют результаты выполнения:

А) 35 — не является результатом при умножении числа 4;

64 — не является результатом при умножении числа 9;

54 — не является результатом при умножении числа 8.

Г) Решение примеров различными способами:

1. Умножение столбиком;

2. Умножение числа на сумму.

Актуализированные знания таблицы умножения.

Г) Актуализированные знания правила умножения двузначного числа на однозначное.

Затруднение при нахождении значения выражения 32•23

Постановка учебной задачи

Организовать побуждающий диалог к формулировке темы, цели урока.

-С какой трудностью столкнулись?

— Почему не можете выполнить умножить?

-Кто может определить тему нашего урока? (Слайд 7)

-Что хотим получить в конце урока?

— Не можем умножить 32 на 23.

Умножение двузначного числа на двузначное.

— Должны научиться умножать на двузначное число

Выявить сознательное противоречие.

Сформулировать тему и цель урока.

Решение учебной задачи

Организовать ситуацию целенаправленного поиска

-Достаточно ли у нас знаний, чтобы решить данный пример?

-Как будем выходить из сложившейся ситуации?

-Кто может помочь решить данный пример?

Мы умеем умножать сумму на число. Попробуйте решить этот пример, используя это правило.

Объясните, какой способ решения вы нашли.

32 * (20+3) = (Слайд 8)

Дети предлагают различные варианты решения.

Хорошо будет предложен вариант использования правила умножения суммы на число.

— Нам могут помочь родители, они точно знают, как его решить.

— Могут помочь учитель.

Групповая работа учащихся по поиску решения. Можно совещаться друг с другом.

-Раскладываем второе слагаемое на сумму разрядных слагаемых. Умножаем на данное число каждое слагаемое. Полученные произведения складываем.

Полученный способ умножения на двузначное число

(поразрядный способ умножения)

«Раскладываем второе слагаемое на сумму разрядных слагаемых. Умножаем на данное число каждое слагаемое. Полученные произведения складываем».

Применение теоретических положений в условиях выполнения упражнений и решения учебных задач

Организовать ситуации оценки успеха в деятельности.

— Прочитайте задание учебника № 35 стр. 17. (Слайд 9)

Рассмотрите решение выражения:

— Правильное решение вы нашли?

— Можем ли мы себя похвалить?

-Какие числа мы можем еще умножать на двузначное число?

— На какие слагаемые разложили второй множитель?

— Почему этот способ называем способом поразрядного умножения?

Задание учебника №36 стр. 17

Запиши произведение, значение которого вычислено способом поразрядного умножения в результате последовательного выполнения следующих двух действий умножения и одного действия сложения.

Работа в тетради на печатной основе №2 стр. 12 № 23.

Найди значение выражения.

Вычисли следующие значения выражений:

Проверка ответов. Если ответы разные, ищем допущенную ошибку.

Чтение задания учениками.

-Мы можем умножать многозначные числа на двузначное число.

Разложили на сумму разрядных слагаемых и умножаем число 412 на каждое разрядное слагаемое числа 21.

Работа учащихся с подробным объяснением хода действий. 184•(3+70)= 184•3+184•70=552+12880=13432.

Дети оценивают правильность решения учебной задачи и переживают ситуацию успеха.

Самостоятельное, использование сформированных умений и навыков

Организовать самостоятельную работу.

— Все ли готовы проверить свое умение умножать на двузначное число? Прочитайте задание

учебника № 37 стр. 18.

« Вычисли значение каждого из следующих произведений способом поразрядного умножения. Для этого представь второй множитель в виде разрядных слагаемых.

658•11 443•21 322•33 1212•34

Учитель наблюдает и управляет ходом работы. По мере необходимости помогает слабым ученикам.

-Давайте проверим правильность вашего решения.

— Задания какого уровня мы выполняли?

— Сколько баллов успешности заработали?

— Какое умение отрабатывали?

Выполняют задания учителя.

Используют способ поразрядного умножения.

Отрабатывают навык умножения.

Проверяют правильность решения с доской (Слайд 10).

— Мы выполняли задания программного уровня, так как мы использовали старые знания в новой, неизвестной нам ситуации. Такие примеры мы не умели решать.

3 балла успешности — за допущенную одну ошибочку,

либо за помощь учителя.

4 балла успешности – за правильное выполнение всех примеров.

Отрабатывали умение умножения многозначного числа на двузначное.

Сформировать навык умножения многозначного числа на двузначное, путем поразрядного умножения.

— А теперь немножко отдохнем после тяжелой работы.

С неба падают снежинки,

Как на сказочной картинке.

Будем их ловить руками

И покажем дома маме.

А вокруг лежат сугробы,

Снегом замело дороги.

Не завязнуть в поле чтобы,

Поднимаем выше ноги.

Обобщение усвоенного и включение его в систему ранее усвоенных знаний, умений и навыков

Организовать деятельность учащихся по решению задач ранее изученного вида с использованием умножения на двузначное число

— Где нам может пригодиться умение умножать на двузначное число?

Давайте попробуем решить задачу Уч. № 40 стр. 18. (Слайд 12)

На складе хранилось 10 упаковок с яблочным соком и 7 упаковок с апельсиновым. В каждой упаковке было по 24 пакетика сока. Сколько всего пакетиков сока в этих упаковках?

— Умеем ли мы решать задачи данного вида?

Если задача не вызвала у вас затруднений, то можете приступать к решению. Если вы не знаете, с чего начать решение и вам требуется карточка — помощник №1 , пожалуйста, возьмите её. (Приложение 1)

Прочитайте еще раз задачу.

Стало ли вам понятно?

Если все еще не понятно, возьмите карточку помощник №2.

Решайте задачу, отвечая на вопросы карточки.

Давайте проверим решение задачи.

— Сколько действий в задачи?

— Что нашли первым действием?

— Что нашли вторым действием?

Какое записали выражение?

— Каким способом вычисления пользовались?

— Почему именно этим приемом пользовались?

Какой ответ задачи?

А теперь попробуйте составить свою задачу по схеме (Слайд13)

( + ) • =

Решите свою задачу и запишите ответ.

Те, кто раньше других справляется с заданием на любом этапе урока, получает дополнительное задание на развитие логического мышления. (Приложение 2)

(При решении задач)

Дети решают задачу.

Первым действием нашли, сколько всего упаковок с яблочным и апельсиновым соком на складе.

Вторым действием нашли, сколько пакетиков сока в этих упаковках.

— При вычислении пользовались способом поразрядного умножения.

Потому что мы не умеем 17 умножить на 24 другим способом.

408 пакетиков сока в этих упаковках.

Составление текста задачи.

Решение задачи в тетради.

Решение задачи по заданной схеме на данный способ решения. изученного ранее вида способом поразрядного умножения.

Организовать ситуацию рефлексии

-Переверните страничку и тетради и вспомните, с чего начался наш урок? (Слайд 14)

-Где возникла трудность?

-Как нашли решение?

-Какую цель ставили перед собой?

Окрасьте сегодняшний урок. У каждого есть свое сердечко.

Красный — радость Жёлтый — приятное Зелёный — спокойное Синий – грустное Фиолетовый – тревожный Оранжевый – удовлетворение Чёрный – неудовлетворение

(Дети раскрашивают сердечко) . (Слайд 15)

Можете обосновать свой выбор.

— Дети перечисляют, чем занимались.

-Мы не смогли умножить 32 на 23.

— Мы разложили второе слагаемое на сумму разрядных слагаемых. При умножении использовали поразрядное сложения.

— Научиться умножать на двузначное число.

— Да, цель достигнута.

Осознанный сформированный способ умножения на двузначное число.

-Молодцы, ребята! Вы сегодня очень хорошо потрудились. Большое вам спасибо за работу.

Домашнее задание упр. Т№2 №25 стр. 13, №27 (Слайд 16)

( + ) • =

1. Сколько всего упаковок с яблочным и апельсиновым соком хранилось на складе?

2. Полученную сумму умножь на количество пакетиков в каждой упаковке.

( + ) • =

На полке стояло несколько тарелок. Сначала взяли из всех тарелок без двух одну третью часть, затем — половину оставшихся тарелок. После этого на полке осталось 9 тарелок. Сколько тарелок было на полке?

Муха-Цокотуха купила самовар и пригласила гостей. Она испекла к чаю несколько ватрушек и 12 булочек. Пришло 16 гостей. Каждый взял либо ватрушку, либо булочку, и оказалось, что это половина приготовленных Мухой-Цокотухой выпечных изделий. Сколько ватрушек испекла Муха-Цокотуха?

Внук спросил дедушку: «Сколько тебе лет?» Он ответил так: «Если к моим годам прибавить половину прожитых лет и еще десяток, то будет 100 лет. Сколько лет дедушке?

Источник