Задача «встреча». Аналитический способ решения
Теперь решим задачу из предыдущего параграфа другим способом – аналитическим. Посмотрим на рис. 20 и вспомним, что было сделано за первые три шага решения этой задачи.
Шаг 1 . Мы ввели систему отсчета: 1) выбрали началом отсчета дерево, от которого начинал свое движение пешеход; 2) направили координатную ось вдоль дороги в направлении движения пешехода; 3) включили часы (секундомер) в момент начала движения тел.
Шаг 2 . Были определены начальные координаты пешехода (xп0 = 0) и велосипедиста (xв0= 20 м).
Шаг 3 . Используя введенную систему отсчета, мы определили значения скоростей движения пешехода (vп = 1 м/с) и велосипедиста (vв = -3 м/с).
Таким образом, первые три шага решения задачи не зависят от того, каким способом (графическим или аналитическим) мы собираемся ее решать. Но уже следующий шаг будет отличаться от того, что мы делали при графическом способе решения.
Шаг 4 (аналитический). Запишем в аналитическом виде законы движения тел, учитывая известные данные. Поскольку в задаче движутся два тела (пешеход и велосипедист), то мы получаем два закона движения:
xп = 0 + 1 · t, xв = 20 — 3 · t.
Шаг 5 (аналитический) . Представим в виде уравнения условие задачи – встречу велосипедиста и пешехода. Встреча двух тел означает, что положения тел в пространстве совпадут в некоторый момент времени t = tвстр, т. е. в этот момент времени совпадут их координаты. Поэтому условие встречи будет иметь вид:
Шаг 6 (аналитический) . Запишем вместе полученные в шагах 4 и 5 выражения, присвоив каждому из них свои номер и название.
xп = 0 + 1 · t, (1) (закон движения пешехода)
xв = 20 — 3 · t, (2) (закон движения велосипедиста)
xп = xв. (3) (условие встречи пешехода и велосипедиста)
Шаг 7 (аналитический). Решение уравнений.
Для того чтобы найти значение времени t в интересующий нас момент встречи, воспользуемся условием встречи пешехода и велосипедиста – уравнением (3). Оно предполагает равенство координат двух тел. Подставим в него выражения для xп и xв из уравнений (1) и (2):
0 + 1 · t = 20 — 3 · t
Приведем подобные слагаемые и решим уравнение:
(1+3) · t = 20, t = 20/4 = 5 (с).
Таким образом, мы установили, что встреча пешехода и велосипедиста состоится через 5 с после начала движения.
Теперь определим координату точки, в которой состоится встреча. Для этого подставим полученное значение момента встречи tвстр = 5 с в закон движения пешехода – уравнение (1):
xп = 0 + 1 · tвстр = 0 + 1 · 5 = 5 (м).
Это означает, что в момент встречи координата пешехода будет равна xп = 5. Следовательно, встреча произойдет в 5 м от начала отсчета – дерева, от которого начал движение пешеход.
Ясно, что координату места встречи можно было определить, подставив время tвстр = 5 с и в закон движения велосипедиста – уравнение (2):
xв = 20 — 3 · tвстр = 20 — 3 · 5 = 5 (м).
Естественно, мы получили то же самое значение хвстр, так как координаты пешехода и велосипедиста в момент встречи совпадают.
Итоги
При аналитическом способе решения задачи «встреча» момент встречи и координата места встречи определяются из равенства координат в законах движения тел, записанных в аналитическом виде.
1. Определите аналитическим способом время и место встречи пешехода и велосипедиста (начните с шага 3) в выбранной нами ранее системе отсчета, связанной с деревом, если:
а) значение скорости пешехода осталось прежним vп = 1 м/с, а велосипедист едет ему навстречу со скоростью |vв| = 4 м/с;
б) значение скорости пешехода vп = 3 м/с, а велосипедист едет со скоростью, значение которой vв = -7 м/с.
2. Выполните предыдущее упражнение, решая задачу графическим способом.
3. Определите аналитическим способом время и координату встречи пешехода и велосипедиста, которые движутся навстречу друг другу со скоростями |vп| = 2 м/с и |vв| = 8 м/с, если начальное расстояние между ними l = 160 м и они начинают движение одновременно. (Начните решение с шага 1.)
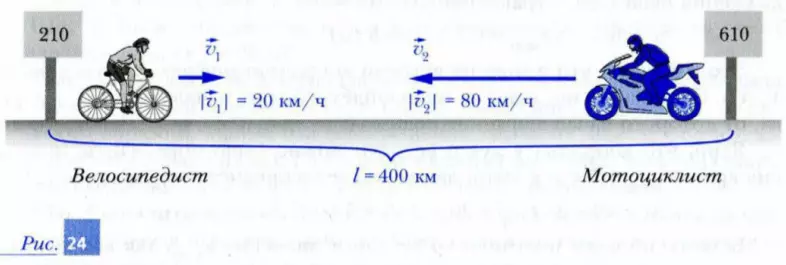
4. Сформулируйте условие и решите задачу о встрече велосипедиста и мотоциклиста, изображенных в момент времени t = 0 на рис. 24.
Источник
Страница 33. Урок 17 — Математика 2 класс. Петерсон Л.Г. Учебник часть 1
Вопрос
Задание № 1. Реши примеры 18 + 35 и 41 — 29: а) с помощью графических моделей; б) в столбик; в) прибавляя и вычитая по частям; г) дополняя до круглого числа. Какой способ ты считаешь самым удобным?
Подсказка
Повтори состав двузначного числа, а также алгоритм письменного сложения и вычитания.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 2. Вычисли и найди в каждом столбике лишний пример:
| 6 + 30 | 28 + 40 | 59 + 31 | 17 + 65 |
| 36 — 6 | 68 — 28 | 59 — 31 | 82 — 17 |
| 36 — 30 | 68 — 0 | 90 — 59 | 82 — 65 |
| 36 — 36 | 68 — 40 | 90 — 31 | 82 + 17 |
Подсказка
Повтори состав двузначного числа.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 3.
а) Составь все возможные равенства 8, 74, 82.
б) Объясни способы проверки примеров на сложение и примеров на вычитание.
Подсказка
Повтори, как называются числа при сложении и вычитании.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 4. Выполни действия:
| 16 — 9 + 23 | 74 — 24 — 8 | 56 + 14 — 45 | 39 + 53 — 28 |
Подсказка
Повтори состав многозначных чисел.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 5. В двух корзинах 50 кг яблок. В первой корзине 32 кг. На сколько килограммов яблок во второй корзине меньше, чем в первой?
Подсказка
Повтори, что такое задача.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 6. Ира с мамой и папой ходили по грибы. Когда они сосчитали собранные грибы, то оказалось, что Ира собрала 20 грибов, мама — на 18 грибов больше, чем Ира, а папа — на 7 меньше, чем мама. Сколько грибов они собрали вместе?
Источник
Выполните предыдущее упражнение решая задачу графическим способом
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
- Главная
- 9-Класс
- Алгебра
- Видеоурок «Графический способ решения текстовых задач»
Существует несколько способов решения текстовых задач: арифметический способ, алгебраический способ,геометрический способ, схематический способ играфический способ.
На этом занятии мы рассмотрим графический способ решения текстовой задачи. Этот способ заключается в решении текстовой задачи с помощью графиков в прямоугольной системе координат. Математическая модель текстовой задачи при графическом методе — это графики, построенные по данным условия задачи. Обычно такими графиками являются прямые. Ответом на главный вопрос задачи служат координаты определённых точек, или величины, связанные с ними. Например, в задачах на встречное движение координаты точек пересечения двух графиков характеризуют место встречи движущихся объектов.
Рассмотрим методику решения текстовых задач графическим способом на примерах.
Пешеход вышел из дома в 8 часов и за 1,5 часа прошёл 6 км. Сколько км пройдёт пешеход за 2 часа 15 минут? Успеет ли пешеход встретить проходящий через станцию поезд в 13 часов 30 минут, если расстояние от его дома до станции 21 км?
1. Зададим прямоугольную систему координат sOt с горизонтальной осью абсцисс Оt и вертикальной осью ординат Os, где по оси Ot будем отмечать время, выраженное в часах, а по оси Os- расстояния, соответствующие времени t.
2. Выпишем условия задачи в виде таблицы. В первой строке таблицы отметим время, во второй строке – расстояния, соответствующие указанному времени. По условию задачи пешеход вышел из дома в 8 часов, значит, начальное положение пешехода соответствует пути S равном 0 при времени t равном 8. Из следующего условия задачи пешеход за 1,5 часа прошёл 6 км следует, что при s, равном расстоянию 8 плюс 6, то есть 14-ти время t равно 1,5. Так как движение пешехода было равномерным, то графиком его движения является луч с началом в точке (8,0), проходящий через точку (1,5;14) соответственно указанным выше условиям. В третьих, выберем удобный масштаб делений для построения точек в плоскости. По оси абсцисс Ot за 1час примем 4 деления, а по оси Os- за 2км примем 1 деление. Отметив точки в координатной плоскости, проведём луч. Таким образом, графиком в виде луча мы смоделировали движение пешехода. Далее по построенному графику несложно определить, что точка с ординатой 21 имеет абсциссу 13,25. А это означает, что на станции в 21км от дома пешеход окажется в 13ч 15мин. По условию поезд должен пройти через станцию в 13 часов 30 минут, значит, пешеход успеет встретить поезд на станции. Мы ответили на неявный вопрос задачи: Успеет ли пешеход встретить проходящий через станцию поезд. Ответим на явный вопрос задачи: Сколько км пройдёт пешеход за 2 часа 15 минут? Для этого найдём точку с абсциссой 8 плюс 2,25 равной 10,25, соответствующей времени 2ч 15минут движения пешехода после выхода из дома. По графику несложно определить её ординату. Она равна 9, то есть 9км пешеход пройдёт за 2ч 15 минут. Таким образом, с помощью графика мы ответили на все главные вопросы задачи.
Рассмотрим ещё одну задачу на применение графического способа её решения.
От посёлка до станции велосипедист выехал со скоростью 10км/ч, а возвращался со скоростью 15км/ч, поэтому он затратил на обратный путь на 1ч меньше. Найдите расстояние от посёлка до станции.
1. Зададим прямоугольную систему координат sOt с горизонтальной осью абсцисс Оt и вертикальной осью ординат Os, где по оси Ot будем отмечать время, выраженное в часах, а по оси Os- расстояния, соответствующие времени t.
2. Определим ключевые точки графиков движения велосипедиста от посёлка до станции и обратно. По условию задачи от посёлка до станции велосипедист выехал со скоростью 10км/ч. Следовательно, график луча движения велосипедиста имеет начало в точке с координатами (0;0) и проходит через точку (1;10), так как скорость 10км/ч означает, что за 1час велосипедист преодолевает 10км пути. Про обратный путь от станции до посёлка сказано, что велосипедист возвращался со скоростью 15км/ч, поэтому он затратил на обратный путь на 1ч меньше. Изобразим это движение в виде луча с началом в точке с координатами (1;0), проходящим через точку (2;15), так как скорость 15км/ч означает, что за каждый час движения он изменяет свой путь на 15км. 3. Выберем удобный масштаб делений на осях координат. По оси абсцисс Ot за 1час примем 1 деление, а по оси Os- за 5км примем 1деление. Построим один луч с началом в точке (0;0), проходящий через точку (1;10), и второй луч с началом в точке (1;0), проходящий через точку (2;15). По графику несложно увидеть, что эти лучи пересеклись в точке с координатами (3;30). Абсцисса этой точки показывает время движения велосипедиста от дома до станции, а её ордината – расстояние от дома до станции. Таким образом, мы ответили на главный вопрос задачи 30км – расстояние от дома до станции.
Разберём решение задачи на движение нескольких видов транспорта.
Из Санкт-Петербурга в Москву выехала легковая машина со средней скоростью 100км/ч. Через 1час 40минут после её отправления из Москвы в направлении Санкт – Петербурга выехал мотоциклист со скоростью 60км/ч. А ещё через 20 минут после мотоциклиста выехал велосипедист из Твери в сторону Санкт-Петербурга со скоростью 10км/ч. Встретятся ли все три вида транспорта в одном месте, если город Тверь расположен на трассе Москва-Санкт-Петербург в 170км от Москвы и в 530км от Санкт-Петербурга? Если встреча произойдёт, то на каком расстоянии от Твери она состоится и сколько времени до встречи проедет мотоциклист?
1. Зададим прямоугольную систему координат sOt с горизонтальной осью абсцисс Оt и вертикальной осью ординат Os, где по оси Ot будем отмечать время, выраженное в часах, а по оси Os- расстояния, соответствующие времени t.
2. Составим таблицу данных по условию задачи. Согласно условию задачи машина начала движение из Санкт-Петербурга раньше всех видов транспорта, значит, начало её движения примем за начало отсчёта системы координат. Скорость машины была 100км/ч, значит, точкой графика её движения будет точка с координатами (1;100), так как она за 1 час проходила 100км. По условию задачи мотоциклист выехал позже на 1час 40минут из Москвы, т.е. 
расстояния от Твери до Москвы и от Твери до Санкт-Петербурга, то есть 170км + 530км. Получили расстояние 700км. Значит, началом графика движения мотоциклиста будет точка с
По условию задачи велосипедист выехал на 20минут позже мотоциклиста, значит, абсцисса начала графика его движения будет равна 
Мотоциклист выехал из Твери в 530-ти км от Санкт-Петербурга, значит, ордината точки начала графика равна 530. По условию задачи мотоциклист двигался в сторону Санкт-Петербурга со скоростью 10км/час, значит, график его движения пройдёт через точку с абсциссой 3+1 равной 4 и ординатой 530 – 10 равной 520.
3. Выберем удобный масштаб делений для построения точек на плоскости. Так как в условии задачи присутствуют доли часа 1час 40 минут, что составляет 
деление. Таким образом, луч движения машины имеет начало в точке с координатами (0;0) и проходит через точку с координатами (1;100), график движения мотоциклиста начинается в 
движения велосипедиста имеет начало в точке с координатами 3 и 530 и проходит через точку с координатами 4 и 520. Построив лучи в одной плоскости, получаем точку пересечения графиков движений с абсциссой 5 и ординатой 500. Это означает, что встреча всех трёх видов транспорта произойдёт через 5 часов после начала движения машины в 500км от Санкт-Петербурга. Несложно определить по графику, что место встречи будет в 30км от Твери, и мотоциклист пробудет в пути до встречи 3часа 20 минут. Мы ответили на главные вопросы задачи.
Таким образом, графический способ решения текстовых задач привлекает отсутствием громоздких вычислений и быстротой получения ответа на главные вопросы задачи. Но при этом методе решения важно уметь выделять числовые данные задачи и моделировать их в координаты точек графиков. Не менее важным здесь является умение выбирать правильный масштаб единиц измерения на осях координат, а также умение считывать информацию с полученной конфигурации графиков. Всё это приходит с опытом при условии частого применения этого способа в решении текстовых задач.
Источник
