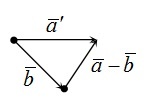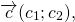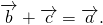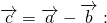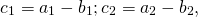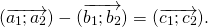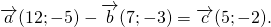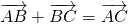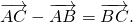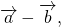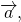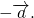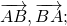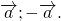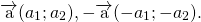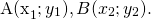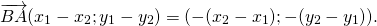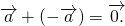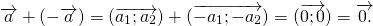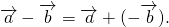Вычитание векторов способом треугольника

Умножение вектора на число

Пусть нам дан вектор \( \overrightarrow \) и действительное число \( k \) .

Определение Произведением вектора \( \overrightarrow \) на действительное число \( k \) называется вектор \( \overrightarrow \) удовлетворяющий следующим условиям:

Длина вектора \( \overrightarrow \) равна \( \left|\overrightarrow\right|=\left|k\right||\overrightarrow| \) ;

Векторы \( \overrightarrow \) и \( \overrightarrow \) сонаправлены, при \( k\ge 0 \) и противоположно направлены, если \( k\le 0 \)

Обозначение: \( \ \overrightarrow=k\overrightarrow \) .

Источник

Вычитание векторов

Как происходит вычитание векторов

Вычитание векторов — это арифметическое действие в геометрии, при котором из одного вектора отнимают другой.

Чтобы вычесть \(\overrightarrow b\) из \(\overrightarrow а\) , нужно найти такой \(\overrightarrow с\) , сложение которого с вектором \(\overrightarrow b\) составляло бы \(\overrightarrow а\) .

Таким образом, формула разности будет выглядеть так:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

\(\overrightarrow а-\overrightarrow b=\overrightarrow а+\left(-\overrightarrow b\right)\)

Если задан \(\overrightarrow а\) , то можно построить противоположный ему \(-\overrightarrow а\) , равный по длине, но противоположно направленный. Тогда происходит сведение двух противоположно направленных векторов к нулевому:

\(\overrightarrow а+\left(-\overrightarrow а\right)=0\)

Как производится вычитание векторов по координатам

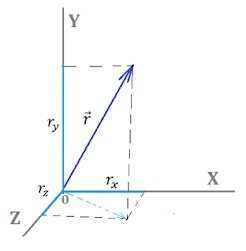
Если необходимо произвести вычитание векторов по координатам, то следует просто вычесть соответствующие точки. То есть если из \(\overrightarrow а\) отнимается \(\overrightarrow b\) , то из X₁ отнимаем X_2, из Y₁ Y₂ и из Z₁ Z₂.

Проиллюстрируем координатное пространство:

Основные правила вычисления

Для того, чтобы найти значение разности векторов, можно использовать несколько способов.

Правило треугольника

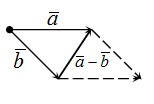
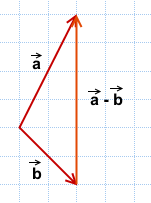
Чтобы графически продемонстрировать разность, необходимо отложить от произвольной точки вектор \(\overrightarrow а\) , из его начала \(\overrightarrow b\) . Тогда вектор, начало которого совпадает с концом \( \overrightarrow b\) , а конец — с концом \(\overrightarrow a\) , и будет искомым вектором разности \(\overrightarrow a\;-\;\overrightarrow b\) . Проиллюстрируем это:

Правило параллелограмма

Если два неколлинеарных, то есть непараллельных вектора \(\overrightarrow а\) и \(\overrightarrow b\) имеют общее начало, то их разностью является вектор, совпадающий с диагональю параллелограмма, построенного на \(\overrightarrow а\) и \(\overrightarrow b\) , причем начало этой диагонали совпадает с концом \(\overrightarrow b\) , а конец — с концом \(\overrightarrow а\) .

Если векторы \(\overrightarrow а\) и \(\overrightarrow b\) заданы в некотором промежутке:

\(\overrightarrow a=\left(а_1;а_2\right),\;\overrightarrow b=\left(b_1;b_2\right)\)

то, чтобы найти координаты их разности \(\overrightarrow a\;-\;\overrightarrow b\) , необходимо от точек \(\overrightarrow a\) отнять соответствующие точки \(\overrightarrow b\) :

\(\overrightarrow a\;-\;\overrightarrow b=\left(a_1;a_2\right)-\left(b_1;b_2\right)=\left(a_1-b_1;a_2-b_2\right)\)

Проиллюстрируем правило многоугольника:

Примеры задач на понятие разности векторов

Задача 1

Дано

\(\overrightarrow a\;=\left(2;-1\right),\;\overrightarrow b=\left(0;2\right)\)

Найти: \(\overrightarrow с=2\overrightarrow a-3\overrightarrow b\;\)

Решение

Найдем координаты \(2\overrightarrow a\) и \(3\overrightarrow b\) . Для этого умножим каждую на два и три:

\(2\overrightarrow а=2\times\left(2;-1\right)=\left(2\times2;2\times\left(-1\right)\right)=\left(4;-2\right), 3\overrightarrow b=3\times\left(0;2\right)=\left(3\times0;3\times2\right)=\left(0;6\right)\)

Тогда искомый вектор:

\(\overrightarrow с=2\overrightarrow a-3\overrightarrow b=\left(4;-2\right)-\left(0;6\right)=\left(4-0;\;-2-6\right)=\left(4;-8\right)\)

Ответ: \(\overrightarrow с=\left(4;-8\right).\)

Задача 2

Дано

Найти: координаты \(\overrightarrow-\overrightarrow.\)

Решение

Для начала найдем проекции \(\overrightarrow\) и \(\overrightarrow\) .

Для этого от координат конца вектора, то есть точек B и D, нужно отнять соответствующие проекции его начала, то есть точек А и С.

Тогда для нахождения координат разности \(\overrightarrow-\overrightarrow\) , от координат первого вычтем координаты второго:

Источник

Разность векторов

Разность векторов

— это такой вектор

который в сумме с вектором b даёт вектор a:

На основе определения находим координаты вектора

Как построить разность двух векторов?

Из равенства

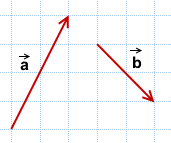
правило построения разности двух векторов

Чтобы построить вектор, равный разности векторов

надо отложить оба вектора от одной точки. Разность векторов — вектор, проведённый от конца вычитаемого b к концу уменьшаемого a.

Противоположные векторы — это противоположно направленные векторы одинаковой длины.

Вектор, противоположный вектору

Примеры противоположных векторов:

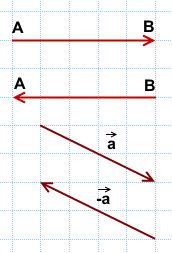
Свойства противоположных векторов:

1) Противоположные векторы имеют противоположные координаты:

Пусть даны точки

2) Сумма противоположных векторов равна нулевому вектору:

2 способ построения разности векторов

Чтобы построить разность векторов

можно к вектору a прибавить вектор, противоположный вектору b:

То есть вычитание векторов заменяем сложением уменьшаемого с вектором, противоположным вычитаемому.

Источник

Вычитание векторов

Средняя оценка: 4.6

Всего получено оценок: 140.

Средняя оценка: 4.6

Всего получено оценок: 140.

Вычитание векторов часто вызывает проблемы у учеников. Это связано с тем, что вычитание в геометрии нужно выполнять очень осторожно, чтобы не получалось отрицательных чисел. А вектор может быть отрицательным, положительным, нулевым – это вызывает много ошибок, которых можно избежать просто один раз разобравшись в вопросе.

Вектор

Вектор – одно из самых интересных явлений в математике. Это первая величина во всем школьном курсе, которая имеет две характеристики: направление и размер. Вектором называют направленный отрезок, то есть отрезок, у которого стрелкой указали направление движения.

Представьте, вы прошли километр от дома до парка. Если поставить точку в начальном положении и стрелку в конечном, то результат движениям будет являться вектором. Ведь он имеет направление: от дом до парка. При этом у результата движения есть и размер, в нашем случае это один километр.

Ученики часто пугаются отрицательных векторов, но в этом нет ничего страшного. Вектор это направление некого движения, а любое движение относительно, то есть зависит от системы отсчета.

В любую систему отчета входит точка отчета, система координат и прибор для измерения времени.

Если вектор поместить в любую систему координат, даже если это будет простой координатный луч, то вектор может быть направлен в одну сторону с системой координат, но может и в разные. Если вектор и система координат направлены в разные стороны, то вектор будет отрицательным.

Рис. 1. Вектор в системе координат.

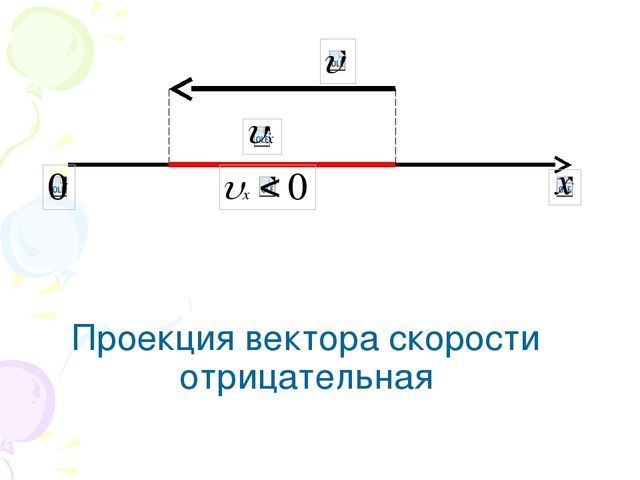
При этом противоположным направлением считается любое в половине плоскости, в другую сторону которой направлен вектор.

Особые случаи векторов

Первый вопрос, который возникает у множества учеников, это возможность существования нуля в системе векторов. Ноль у векторов есть, только это не число, а точка. Любую точку можно считать нулевым вектором. Нулевой вектор появляется в результате сложения коллинеарных разнонаправленных векторов.

Коллинеарными называют вектора, которые лежат на одной прямой. Эти векторы могут быть сонаправлены или противоположно направлены. При этом векторы, которые лежат на одной прямой так же считаются коллинеарными, так как любая прямая параллельна самой себе. Это не трудно понять, но запомнить название лучше наизусть, так как в тематике векторов, это определение встречается довольно часто.

Результат сложения или вычитания коллинеарных векторов будет коллинеарным для каждого из начальных построений. Поэтому найти результат такой операции можно арифметически, да и построить треугольник или параллелограмм из коллинеарных векторов не получится.

Вычитание векторов

Результатом вычитания векторов может быть:

• Вектор. Если вычитание производилось в системе координат, то результат может быть положительным или отрицательным
• Нулевой вектор или точка
• Никаких других результатов быть не может

Рис. 3. Вычитание векторов.

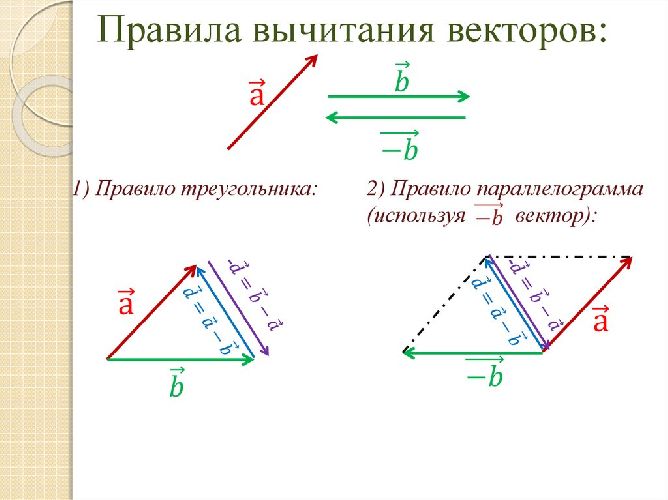
Для того, чтобы вычесть один вектор из другого, любой из векторов заменяется на противоположный и выполняется сложение по правилу треугольника или параллелограмма. Таким образом, меняется знак вектора.

В математической записи это выглядит так:

АВ-МР=АВ+РМ – в математической записи первая буква означает начало вектора, вторая – конец. Так можно без чертежа обозначить направление.

Что мы узнали?

Мы поговорили о векторах и их частных случаях. Обсудили, как правильно вычитать вектора и что может получиться в результате такого вычитания. Привели пример правильной записи вычитания 2 векторов.

Источник