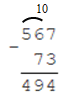Вычитание удобным способом 5 класс примеры

Вычитание натуральных чисел. Свойства вычитания.
методическая разработка по математике (5 класс)

Данная практическая работа составлена из примеров на применение различных правил вычитания, некоторые правила сопровождаются картинками, одно из заданий носит творческих характер, поскольку учащимся предлагается самим придумать примеры на все рассматриваемые правила.

Скачать:

Вложение	Размер
svoystva_vychitaniya_chisel.docx	14.25 КБ

Предварительный просмотр:

Вычитание натуральных чисел. Свойства вычитания.

№ 1. Используя свойство прибавления к уменьшаемому и вычитаемому одного и того же числа, вычислите:

№ 2. Используя правило вычитания суммы из числа, вычислите:

№ 3. Используя правило вычитания числа из суммы, вычислите:

б) (444 + 269) — 269

в) (947 + 486) – 847

№ 4. Вычислите удобным способом:

д) (386 + 139) — 286

ж) (3408 + 2891) – 791

№ 5 * . Придумайте название данным правилам, попробуйте их сформулировать. Приведите примеры.

1. а – в = (а + с) – (в + с)
2. а — в = (а — с) – (в – с)
3. а – а =0
4. а — 0 = а
5. а – ( в + с) = а – в – с
6. (а + в) – с =( а – с) + в = а + (в – с)

По теме: методические разработки, презентации и конспекты

Презентация к уроку математики в 5 классе «Буквенная запись свойств сложения и вычитания натуральных чисел».

урок систематизации и комплексного применения знаний, умений и навыков (урок повторения курса начальной школы.Основными целями ставятся:Особобщения и систематизации знаний по заданной теме, испо.

Обобщающий урок с элементами игровых технологий.

Открытый урокпо математике в 5 а классеМОУ « СОШ ст. Тарханы »по теме:« Вычитание натуральных чисели его свойства». Подготовила и провелаучитель математики первой квалифика.

Технологическая карта урокаУчитель Каргина Ирина ПетровнаПредмет математикаКласс.

Технологическая карта урокаУчитель Каргина Ирина ПетровнаПредмет математикаКласс.

Технологическая карта урокаУчитель Каргина Ирина ПетровнаПредмет математикаКласс.

Источник

Вычитание натуральных чисел

Понятие «вычитание»

Вычитание — одно из четырех арифметических действий. Вычитание записывают при помощи знака «-» минус.

Например: 34 — 13 = 21

Вычитание — действие обратное сложению.

То есть, 25 — 6 = 19 ⇔ 19 + 6 = 25

Обозначения

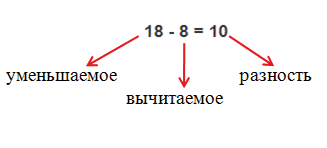
Число из которого вычитают, называется уменьшаемым. 18 — уменьшаемое.

Число, которое вычитают, называется вычитаемым. 8 — вычитаемое.

Результат вычитания, называется разностью. 10 — разность.

Свойства вычитания натуральных чисел

1) При вычитании натуральных чисел уменьшаемое всегда должно быть больше вычитаемого.

100 — 60 = 40 100 — 101 = не натуральное число

2) Разность показывает на сколько больше уменьшаемое больше вычитаемого.

34 больше, чем 7 на 17 единиц.

3) Если вычитаемое равно 0, разность равна уменьшаемому.

4) Если от любого числа вычесть 1, то получим число предшествующее данному.

5) Вычитание натурального числа из суммы натуральных чисел.

Чтобы вычесть натуральное число из суммы натуральных чисел, необходимо сначала сложить числа, а затем вычесть данное натуральное число, или первым действием вычесть данное натуральное число из любого слагаемого, а к разности прибавить оставшееся слагаемое.

(26 + 9) — 6 = 26 — 6 + 9

6) Вычитание суммы чисел из натурального числа.

Чтобы вычесть сумму чисел из натурального числа, необходимо сначала сложить два числа, после этого вычесть полученную сумму из данного числа, или вычесть из данного числа любое из слагаемых, поле этого вычесть второе.

47 — (16 + 7) = 47 — 7 — 16

Вычитание чисел с разными разрядами

Для того чтобы вычесть числа с разным разрядом, необходимо разложить числа по разрядам.

567 = 500 + 60 + 7 = 400 + 100 + 60 + 7

Из единиц вычтем единицы, из десятков десятки, из сотен сотни и т.д.

7 — 3 = 4;

Поскольку из 60 нельзя вычесть 70, разложим 500 на 400 и 100, прибавим 100 к 60

(100 + 60) — 70 = 90;

400 — 0 = 400.

Полученное число: 400 + 90 + 4 = 494.

Вычитание в столбик

Многозначные числа удобнее всего вычитать в столбик. Для того чтобы вычесть число из числа в столбик, необходимо:

1. Правильно записать числа. Первым записываем уменьшаемое, под уменьшаемым пишем вычитаемое, так чтобы каждый разряд вычитаемого находился строго под соответствующим разрядом вычитаемого. Слева поставим знак «-» под столбиком, состоящим из уменьшаемого и вычитаемого проводим черту

2. Справа налево последовательно вычитаем из разряда уменьшаемого соответствующий разряд вычитаемого. Результат запишем под чертой, это будет разность.

3 Если разряд уменьшаемого окажется меньше разряда вычитаемого занимаем 10 у разряда стоящего слева (см. рисунок).

Вычитание с помощью координатного луча

Для вычитания с помощью координатного луча, отметим точку соответствующую уменьшаемому, в нашем примере, это число 12. Для вычитания отсчитываем влево количество единичных отрезков равных вычитаемому (8). Получившаяся точка будет являться разницей (4).

Поделись с друзьями в социальных сетях:

Источник

Математика. 5 класс

Конспект урока

Перечень вопросов, рассматриваемых в теме:

— понятие разности двух чисел;

— вычитание натуральных чисел;

— проверка правильности вычитания – сложением;

— свойство прибавления к уменьшаемому и вычитаемому одного и того же числа.

Разность чисел a и b – это такое число, которое при сложении с числом b даёт число а. Число а называют уменьшаемым, число b – вычитаемым.

Чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности – второе слагаемое.

Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое. Стоит помнить, что вычитаемое должно быть не больше слагаемого, из которого его вычитают.

Если к уменьшаемому и вычитаемому одновременно прибавить одно и то же число, то разность от этого не изменится.

1. Никольский С. М. Математика: 5 класс. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2017. – 272 с.
2. Потапов М. К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.

1. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
2. Потапов М. К. Математика: дидактические материалы. 6 класс. // М. К. Потапов, А. В. Шевкин – М.: Просвещение, 2010.- 118 с.
3. Чесноков А. С. Дидактические материалы по математике 5 класс. // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.

Теоретический материал для самостоятельного изучения

Разностью чисел a и bназывают такое число, которое при сложении с числом b даёт число а. Число а называют уменьшаемым, число b – вычитаемым.

Разность чисел а и b обозначают а – b.

Таким образом, (а – b) + b = a или а – b + b = a.

Рассмотрим, как, используя числовую прямую, можно найти разность натуральных чисел а и b в случае, когда a>b.

Пусть нам надо найти разность 8 – 5. Отметим на числовом луче число 8 и отсчитаем от него влево пять делений. Получим число 3.

Мы видим, что сумма 3 и 5 равна 8.

Поэтому число 3 есть разность чисел 8 и 5, то есть 8 – 5 = 3.

Стоит отметить, что для любого числа a верны равенства:

а – 0 = а, потому что а + 0 = а

а – а = 0, потому что 0 + а = а

При действиях с натуральными числами уменьшаемое не может быть меньше вычитаемого.

Разность двух чисел показывает, на сколько первое число больше второго, иными словами, на сколько второе число меньше первого.

Рассмотрим такой пример: 12 – (3 + 4) = 12 – 3 – 4 = 5.

Чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности – второе слагаемое. Это свойство называют свойством вычитания суммы из числа.

Рассмотрим следующее выражение: (6 + 5) – 4 = 6 + 5 – 4 = 7

Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое. Стоит помнить, что вычитаемое должно быть не больше слагаемого, из которого его вычитают. Это свойство называют свойством вычитания числа из суммы.

Найдём разность двух сумм:

(7 + 2) – (4 + 2) = 9 – 6 = 3 или

(7 + 2) – (4 + 2) = 7 + 2 – 4 – 2 = 3.

Это свойство прибавления к уменьшаемому и вычитаемому одного и того же числа: если к уменьшаемому и вычитаемому одновременно прибавить одно и то же число, то разность от этого не изменится, то есть (a + n) – (b + n) = a–b.

Разбор решения заданий тренировочного модуля

№ 1.Чему равно значение выражения: 139 – 42 – 63? Выберите правильный ответ.

Варианты ответов: 34; 97; 90; 134.

Решение: чтобы решить данное выражение, надо вычесть 42 из 139, что даст 97, а затем ещё раз вычесть 63. В итоге получим 34.

№ 2. Путешественник должен пройти 56 км. В первый день он прошёл 27 км. Сколько км ему ещё осталось пройти?

Решение: чтобы узнать сколько километров осталось пройти путешественнику, необходимо из 56 вычесть 27: так получим 29 (км).

Источник

Урок 13 Бесплатно Вычитание натуральных чисел. Способы вычитания натуральных чисел

На этом уроке продолжим разговор о вычитании натуральных чисел.

Вспомним название компонентов арифметической операции вычитания и установим, по каким правилам находится каждое из них.

Познакомимся с различными способами и приемами вычитания, закрепим полученные знания на примерах.

Взаимосвязь компонентов арифметической операции вычитания

Каждый компонент арифметической операции вычитания имеет свое название.

У меня есть дополнительная информация к этой части урока!

Уменьшаемое — число, из которого вычитают.

Вычитаемое- число, которое вычитают из уменьшаемого.

Разность- результат арифметической операции вычитания (число, составляющее остаток в вычитании)

Часто приходится сталкиваться с ситуацией, когда один из компонентов операции вычитания неизвестен.

Выясним, по каким правилам можно определить каждый из компонентов вычитания.

1. Так как разность- это результат, полученный при выполнении вычитания, то очевидно, что разность находят с помощью данной арифметической операции.

На яблоне висело 12 яблок, 4 яблока упало.

Сколько яблок осталось на яблоне?

12 яблок (исходное количество яблок)- уменьшаемое.

4 яблока (часть яблок)- вычитаемое.

Разность (остаток яблок)?

Ответ: 8 яблок осталось на яблоне.

2. Известно, что уменьшаемое- это число, которое уменьшают, отняв от него некоторую часть.

Следовательно, если из целого вычитают одну часть, то остается еще одна часть, которая образуется в итоге.

Значит, из этих двух частей состоит исходное число.

Таким образом, если неизвестно уменьшаемое число, необходимо сложить два известных компонента вычитания.

Правило: чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.

Мише мама дала конфеты.

Мальчик решил конфетами угостить своего друга Сашу.

После того как Миша отдал 1 конфету, у него осталось 2.

Сколько всего конфет дала Мише мама?

1 конфета (часть конфет)- вычитаемое.

2 конфеты (оставшееся часть конфет)- разность.

Уменьшаемое (всего конфет)?

Ответ: 3 конфеты дала мама Мише.

3. Вычитаемое- это часть, которую отнимают от уменьшаемого.

Если из целого вычитают одну часть, то остается вторая часть этого целого.

Значит, из этих двух частей состоит исходное уменьшаемое число.

Таким образом, если из исходного уменьшаемого числа вычесть одну из частей, то в итоге получается вторая часть.

Правило: чтобы найти вычитаемое, нужно от уменьшаемого отнять разность.

Катя пошла в магазин за хлебом.

Мама дала Кате 25 рублей.

После того, как девочка купила хлеб, у нее осталось 5 рублей.

Сколько Катя заплатила за хлеб?

25 рублей (всего)- уменьшаемое.

5 рублей (осталось)- разность.

Вычитаемое (часть денег, которые отдала Катя за хлеб)?

Ответ: 20 рублей Катя заплатила за хлеб.

Пройти тест и получить оценку можно после входа или регистрации

Способы вычитания натуральных чисел

В современном мире очень важно уметь точно, легко и быстро осуществлять математические вычисления как устно, так и письменно.

В любой сфере человеческой деятельности применяется счет и математические вычисления.

Например, невозможно построить дом, сделать в нем ремонт, определить расстояние и время, купить, продать, приготовить еду и т.д.

Чтобы считать и делать вычисления легко и быстро, необходимо знать и уметь применять основные способы арифметических вычислений и правила счета.

Рассмотрим некоторые способы и приемы, позволяющие верно, быстро и легко вычислить разность натуральных чисел.

Все основные свойства вычитания натуральных чисел, которые нами были рассмотрены уроком ранее, используют для рационального вычисления математических выражений.

Необходимо помнить, что в выражениях, в которых есть скобки, первым делом выполняют те действия, которые находится в этих скобках.

Если в выражении нет скобок и оно содержит сложение и вычитание, то их выполняют по порядку слева направо.

1. Таблица сложения/вычитания натуральных чисел.

Таблица сложения натуральных чисел используется не только для определения суммы чисел от 1 до 10, но и позволяет найти разность чисел, т.е. найти неизвестное слагаемое по известной сумме и второму слагаемому.

Разберемся, что это за таблица и как правильно пользоваться данной таблицей для нахождения разности натуральных чисел.

Таблица представляет собой квадрат, разбитый на десять строк и десять столбцов.

По верхнему краю и по левому краю пронумерованы ячейки от 1 до 10.

Например, определим неизвестное слагаемое, если сумма равна 15, а известное слагаемое равно 9; другими словами, найдем разность чисел 15 — 9.

Уменьшаемое 15.

Вычитаемое 9.

Чтобы определить разность чисел 15 и 9, необходимо найти в первом столбце ячейку со значением 9.

В строке, к которой относится эта ячейка, надо найти ячейку со значением 15, далее необходимо двигаться от этого числа вверх по столбцу до самой верхней строки, на пересечении данного столбца и строки находится ячейка со значением 6 — это и есть разность чисел 15 и 9.

15 — 9 = 6.

Таким же образом можно найти разность 15 и 9. Если вычитаемое 9 находится в ячейке первой верхней строки, то затем в столбце, к которому эта ячейка относится, находим ячейку со значением 15, далее необходимо двигаться от найденной ячейки 15 влево по строке до первого столбца, на пересечении данной строки и столбца находится ячейка со значением 6— это искомая разность чисел 15 и 9.

15 — 9 = 6

Таблицу можно применять при вычитании многозначных чисел по разрядам.

Если условно принять, что в таблице складывается десятки с десятками или сотни с сотнями, или тысячи с тысячами и т.д.

Например, найдем разность 140-60.

Каждые 10 единиц одного разряда составляют одну единицу следующего более высокого разряда.

С помощью таблицы уже известным способом найдем разность чисел 14 и 6, ячейка со значением 8 будет являться разностью чисел 14 и 6.

Условно представим, что ячейка со значением 14— это 14 десятков, ячейка со значением 6 означает 6 десятков.

Тогда разность 14 десятков и 6 десятков равна 8 десяткам.

140 — 60 = 80

Ответ: 80.

2. Способ поразрядного вычитания натуральных чисел

Рассмотрим еще один способ определения разности чисел.

Любое натуральное число можно записать в виде суммы разрядных слагаемых.

Рассмотрим алгоритм поразрядного вычитания натуральных чисел.

1. Уменьшаемое и вычитаемое разложить на разрядные слагаемые.

2. Выполнить вычитание одноименных разрядов (из единиц единицы, из десятков десятки и т.д.)

3. Если число единиц какого-либо разряда вычитаемого больше числа единиц того же разряда уменьшаемого, то для уменьшаемого заимствуется единица высшего разряда.

Каждые 10 единиц одного разряда составляют одну единицу следующего (более высокого разряда)

Найдем разность чисел 673 и 436.

Разложим уменьшаемое и вычитаемое на разрядные слагаемые.

Уменьшаемое: 673 = 6 сотен+7 десятков+3 единицы = 600 + 70 + 3

Вычитаемое: 436 = 4 сотни+3 десятка+6 единиц = 400 + 30 + 6

Из трех единиц уменьшаемого не получится вычесть шесть единиц вычитаемого, следовательно, в разряде десятков уменьшаемого числа занимаем один десяток ( 10 ) и добавляем его в разряд единиц этого уменьшаемого.

Выполним вычитание одноименных разрядов.

673 — 436 = (600 — 400) + ((70 — 10 ) — 30) + (3 + 10 — 6) = 200 +( 60 — 30) + (13 — 6) = 200 + 30 + 7 = 237

Получаем 673 — 436 = 237.

Ответ: 237.

Рассмотренный способ поразрядного вычитания довольно громоздкий в оформлении и не очень удобный для определения разности больших чисел.

3. Способ поразрядного вычитания натуральных чисел «столбиком».

Вычитание многозначных чисел удобно производить в столбик.

Разберемся, что представляет собой данный способ вычитания натуральных чисел.

Для вычитания натуральных чисел «столбиком» необходимо:

1. Знать свойства вычитания натуральных чисел:

Вычитание нуля из натурального числа.

Вычитание из натурального числа само это число.

Вычитание суммы из натурального числа.

Вычитание из натурального числа суммы.

2. Знать и уметь определять разряды натуральных чисел.

Чтобы вычитать натуральные числа «столбиком», нужно уменьшаемое и вычитаемое расположить друг под другом в столбик так, чтобы под уменьшаемым располагалось вычитаемое.

Причем цифры одинаковых разрядов должны стоять друг под другом, т.е. самая правая цифра одного числа (разряд единиц уменьшаемого) должна располагаться под самой правой цифрой другого числа (разряд единиц вычитаемого) далее десятки под десятками, сотни под сотнями и т.д.

Слева между уменьшаемым и вычитаемым ставится знак минус «-».

Под вычитаемым проводят черту.

Разность записывают под чертой.

Итак, вычисление разности натуральных чисел «столбиком» заключается в последовательном вычитании одноименных разрядов, начиная с единиц.

Результаты промежуточных значений записываются под горизонтальной чертой, под тем разрядом, в котором выполнялось действие.

Натуральное число, которое образуется после завершения операции вычитания под чертой, является разностью исходных чисел.

Найдите разность чисел 82030649 и 940565.

82030649— уменьшаемое.

940565— вычитаемое.

Запишем данные числа в столбик.

Между числами поставим знак минус «-», под вычитаемым проведем черту.

1. Начинаем вычитание с простых единиц (самый крайний правый столбец).

9 единиц — 5 единиц = 9 — 5 = 4.

Число 4 записываем в столбик под горизонтальной прямой в разряд единиц.

2. Продолжаем вычисление.

На этом этапе вычитания «столбиком» значение разряда уменьшаемого числа меньше, чем значение одноименного разряда вычитаемого (разность найти невозможно, так как вычитание натуральных чисел справедливо лишь тогда, когда уменьшаемое больше вычитаемого).

В таком случае «занимают» десяток единиц из старших разрядов.

В нашем примере из 4 десятков необходимо вычесть 6 десятков.

Следовательно, чтобы осуществить вычитание единиц данного разряда, нужно занять одну единицу из старшего разряда.

У разряда сотен занимаем одну сотню = 10 десятков.

В таком случае над разрядом сотен в дополнительной строке ставится точка, чтобы запомнить занятую единицу.

Получаем, десять десятков, которые были заняты у соседнего разряда, складываем их с 4 десятками уменьшаемого:

10 + 4 = 14

Из этого числа вычитаем число 6, стоящее в разряде десятков вычитаемого числа.

14 — 6 = 8

Число 8 записываем как результат промежуточного значения под горизонтальной чертой в столбец разряда десятков.

3. Переходим к следующему столбцу- разряд сотен.

Над 6 стоит точка, которая означает, что от этого числа была отнята единица. Таким образом, получаем вместо 6 только 5 сотен.

Вычитаем: 5 — 5 = 0

Число 0 записываем под горизонтальной чертой в столбце соответствующего разряда (разряд сотен).

4. Вычитаем значения разряда тысяч:

0 — 0= 0

Записываем число 0 под чертой в столбик соответствующего разряда.

5. Из 3 нельзя вычесть 4, так как число 3 меньше 4.

Занимаем разрядную единицу у старшего разряда.

Но в соседнем слева разряде единиц нет, стоит нуль.

Ставим над нулем точку и занимаем единицу у следующего по порядку разряда.

Занимаем единицу в разряде миллионов, ставим над 2 точку.

Получаем, десять десятков тысяч, которые были заняты у соседнего разряда, складываем с 3 десятками тысяч уменьшаемого.

Получаем следующее: 10 + 3 = 13

Теперь из 13 легко отнять 4.

13 — 4 = 9

Полученное число записываем под горизонтальной прямой в соответствующем разряде.

6. Занятая единица седьмого разряда равна 10 единицам шестого разряда.

Взяв из них одну единицу для пятого разряда, в результате осталось только 9 единиц в шестом.

Из 9 оставшихся в уменьшаемом вычитаем 9 единиц шестого разряда вычитаемого.

9 — 9 = 0

Запомним, если при вычитании в столбик над нулем стоит точка, то нуль превращается в 9.

7. На последнем шаге вычитания заметим, что над числом 2 стоит точка, которая означает, что была занята единица, т.е. получаем 2 — 1 = 1.

Но из числа больше ничего не нужно вычитать, так как вычитаемое больше не содержит цифр в следующих разрядах.

Таким образом, записываем найденное промежуточное значение равное 1 под чертой в соответствующем разряде.

От числа 8 уменьшаемого также нечего отнимать, и не было занятых единиц, следовательно, число 8 просто сносим под черту.

Вычитание двух натуральных чисел 82030649 и 940565 завершено, разность равна 81090084.

Ответ: 81090084.

У меня есть дополнительная информация к этой части урока!

Вычитание натурального трехзначного числа из 1000.

Для того чтобы быстро и легко вычесть любое трехзначное число из 1000, можно воспользоваться таким правилом:

Все цифры вычитаемого по очереди вычесть из 9, кроме последней (крайней правой) цифры в числе.

Последнюю цифру необходимо вычесть из 10.

Найдем разность чисел 1000 и 467.

9 — 4 = 5

9 — 6 = 3

10 — 7 = 3

Получаем: 1000 — 467 = 5 3 3

Ответ: 533

4. Округления натуральных чисел при вычитании.

Округление числа применяют, когда уменьшаемое или вычитаемое близко к круглому.

Число, которое оканчивается на нуль или несколько нулей, называют круглым числом.

Известно, что круглые натуральные числа упрощают математические вычисления.

Разность не изменится, если к уменьшаемому и вычитаемому прибавить одинаковое количество единиц или отнять одно и тоже количество единиц.

Пример №1.

Найдем разность 47 и 29.

47 — 29 = ?

Число 29 (вычитаемое) близко к круглому числу, увеличим его на единицу.

Для получения верного решения заданного выражения необходимо на единицу увеличить и 47 (уменьшаемое число).

47 — 29 = (47 + 1) — (29 + 1) = 48 — 30 = (40 + 8) — 30 = (40 — 30) + 8 = 10 + 8 = 18

Ответ: 18

Пример №2.

Найдем разность 42 и 18.

42 — 18 = ?

Число 42 (уменьшаемое) близко к круглому числу, уменьшим его на 2 единицы, округлив его до 40.

Для получения верного решения заданного выражения необходимо на 2 единицы уменьшить и 18 (вычитаемое число).

42 — 18 = (42 — 2) — (18 — 2) = 40 — 16 = 40 — (10 + 6) = 40 — 10 — 6 = 30 — 6 = (20 + 10) — 6 = 20 + (10 — 6) = 24

Ответ: 24.

Пройти тест и получить оценку можно после входа или регистрации

Дополнительная информация

Умеют ли животные считать?

Выяснить, способны ли животные считать, не очень просто.

Однако существуют некоторые успешные эксперименты, и собраны доказательства, подтверждающие способность животных обучаться счету и осуществлять некоторые простые вычислительные операции.

Например, результаты исследований убедили ученых Колумбийского университета в том, что шимпанзе умеют считать до пяти.

Обезьяне, которую продолжительное время обучали считать, предложили вынуть из коробочки определенное количество палочек по требованию экспериментатора.

Исследователь попросил у обезьяны 5 палочек, а в коробке лежало всего 4 палочки.

Обезьяна, подумав некоторое время, сломала одну палочку и отдала человеку 5 штук.

Многие животные могут справиться с простейшей математической операцией сравнения небольших чисел.

Ученые из Британского университета проводили ряд экспериментов со львами и выяснили, что львы легко определяют на сколько их прайд отличается по численности от другого.

Экспериментально было определено следующее: львы нападают на «чужаков» в том случае, когда численность вражеских особей не превосходит по численности их прайд.

Подобные исследования проводились с гиенами, результаты ученые получали схожие.

Геены были способны определить как количество звуков, так и количество объектов.

Среди млекопитающих умение считать и сравнивать (определять больше-меньше) проявляли дельфины, слоны, собаки и т.д.

Благодаря множеству исследований и экспериментов ученые делали выводы, что считать могут не только животные, но и птицы, и насекомые.

Например, несколько лет в Аризонском университете (США) изучали способности африканского серого попугая по кличке Алекс.

Попугай научился считать до восьми.

Из небольшого количества кубиков красного и синего цвета Алекс мог ответить на вопрос о том, сколько синих кубиков.

Исследования с голубями подтвердили предположение о том, что они способны считать до шести.

Голубю предлагали зерна, выкладывая по одному, и после каждого шестого давали одно испорченное (непригодное в пищу).

Голубь быстро стал определять каждое седьмое зернышко, он отказывался его пробовать.

Успешные эксперименты были проведены с воронами, которые обитают в Новой Колледонии.

Птицы эти оказались очень разумными.

Немецкие ученые выяснили, что эти вороны могут считать до пяти, и у них есть область мозга, отвечающая за работу с абстрактными числами.

Некоторые птицы способны распознавать количество яиц в гнезде.

Например, если небольшой водоплавающей птице Лысухе в гнездо подкладывают чужие яйца, она выбрасывает из гнезда лишние яйца, а такое же количество своих докладывает.

Эксперименты с насекомыми показали, что некоторые математические способности есть у пчел и муравьев.

Например, исследователь Британского университета установили, что пчелы очень быстро смогли запомнить и определить сладкий сюрприз, расположенный после каждого третьего объекта.

Существует немало других интересных исследований, доказывающих удивительные математические способности окружающего нас животного мира.

Заключительный тест

Пройти тест и получить оценку можно после входа или регистрации

Источник