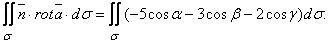Вычислить циркуляцию векторного поля вдоль контура двумя способами

&nbsp &nbsp &nbsp &nbsp Вариант 1 &nbsp &nbsp Вариант 2 &nbsp &nbsp Вариант 3 &nbsp &nbsp Вариант 4 &nbsp &nbsp Вариант 5 &nbsp &nbsp Вариант 6

&nbsp &nbsp &nbsp &nbsp Вариант 7 &nbsp &nbsp Вариант 8 &nbsp &nbsp Вариант 9 &nbsp &nbsp Вариант 10 &nbsp &nbsp Вариант 11 &nbsp &nbsp Вариант 12

&nbsp &nbsp Вариант 13 &nbsp &nbsp Вариант 14 &nbsp &nbsp Вариант 15 &nbsp &nbsp Вариант 16 &nbsp &nbsp Вариант 17 &nbsp &nbsp Вариант 18

&nbsp &nbsp Вариант 19 &nbsp &nbsp Вариант 20 &nbsp &nbsp Вариант 21 &nbsp &nbsp Вариант 22 &nbsp &nbsp Вариант 23 &nbsp &nbsp Вариант 24

&nbsp &nbsp Вариант 25 &nbsp &nbsp Вариант 26 &nbsp &nbsp Вариант 27 &nbsp &nbsp Вариант 28 &nbsp &nbsp Вариант 29 &nbsp &nbsp Вариант 30

&nbsp &nbsp &nbsp &nbsp 12.14 Найти модуль циркуляции векторного поля 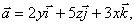&nbsp &nbsp
вдоль контура
&nbsp &nbsp

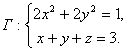
Решение

&nbsp &nbsp &nbsp &nbsp Согласно формуле Стокса:

.
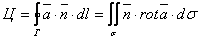
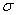
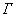
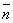
&nbsp &nbsp &nbsp &nbsp Здесь &nbsp &nbsp &nbsp &nbsp — участок поверхности, ограниченный контуром &nbsp &nbsp &nbsp &nbsp , &nbsp &nbsp &nbsp &nbsp — единичный вектор нормали к данной поверхности.

&nbsp &nbsp &nbsp &nbsp Найдём ротор векторного поля

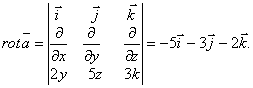
&nbsp &nbsp &nbsp &nbsp Тогда интеграл запишется

&nbsp &nbsp &nbsp &nbsp Здесь &nbsp &nbsp &nbsp &nbsp — направляющие косинусы нормали к поверхности или координаты единичного вектора нормали.
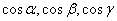
&nbsp &nbsp &nbsp &nbsp Из общего уравнения плоскости запишем координаты нормального вектора 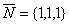&nbsp &nbsp &nbsp .
&nbsp &nbsp &nbsp &nbsp Находим длину нормального вектора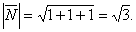
.
&nbsp &nbsp &nbsp &nbsp Тогда направляющие косинусы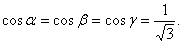
.

&nbsp &nbsp &nbsp &nbsp Элемент поверхности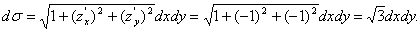
.

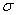
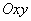
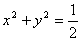
&nbsp &nbsp &nbsp &nbsp Проекцией поверхности &nbsp &nbsp &nbsp &nbsp на плоскость &nbsp &nbsp &nbsp &nbsp является круг

&nbsp &nbsp &nbsp &nbsp Этот круг имеет центр в начале координат и радиус 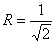&nbsp &nbsp &nbsp &nbsp.

&nbsp &nbsp &nbsp &nbsp Площадь данного круга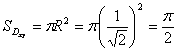
.
&nbsp &nbsp &nbsp &nbsp Переходя от поверхностного интеграла к двойному, получим

&nbsp &nbsp &nbsp &nbsp Тогда модуль циркуляции 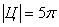&nbsp &nbsp &nbsp .
&nbsp &nbsp &nbsp &nbsp Ответ: Модуль циркуляции равен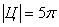&nbsp &nbsp &nbsp .

Источник

Примеры решений задач по теории поля

В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):

Примеры: базовые понятия теории поля

Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.

Задача 2. Найти дивергенцию и ротор векторного поля $\overline=(3x-y) \overline+(6z+5x) \overline$

Задача 4. Вычислить потенциальную функцию векторного поля

Поток поля через поверхность

Циркуляция векторного поля

с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).

Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$. $$ \overline = (3x-1) \overline+ (y-x+z)\overline+4z \overline, $$ $L$ — контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.

Работа векторного поля

Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.

Задача 14. Вычислить работу векторного поля силы $\overline = xz \overline -\overline+y \overline$ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y \ge 0)$ от точки $M(\sqrt(3);0;1)$ до точки $N(-\sqrt(3);0;1)$.

Типовой расчет по теории поля

Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.

$$ \overline = z \overline+ (x+y)\overline+y \overline, \quad (p): 2x+y+2z=2. $$

Помощь с решением заданий

Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей , оформление производится в Word, срок от 1 дня.

Источник

Типовой расчет по математике Векторный анализ

Опр. Циркуляцией векторного поля. (M) = вдоль замкнутой кривой L наз. криволинейный интеграл от скалярного произведения вектора поля и дифференциала радиус-вектора перемещающегося вдоль кривой

Ц L = = ( 32 )

Физический смысл циркуляции — работа по перемещению тела в поле переменных сил по произвольной замкнутой траектории, т.к. работа есть скалярное произведения вектора силы и вектора смещения.

Пусть в векторном поле замкнутый контур L проходит через точки А, B, C, D. Линией АС разделим его на два контура L1, L2 . Тогда циркуляцию вдоль L можно представить как сумму

циркуляций вдоль малых контуров при одинаковом направлении прохождения. Действительно,

Ц1 + Ц2 = + + + = + = Ц L

т.к. общую границу АС проходим дважды в противоположных направлениях. Т.о., циркуляция по контуру L является аддитивной величиной и может быть представлена как сумма циркуляций по малым контурам, полученным путем наложения сетки линий на контур L. В пределе малым участком может оказаться отдельная точка. Тогда циркуляция по контуру сведется к сумме циркуляций вокруг всех точек охваченных контуром L.

Читайте также: Побелка клеевая способ применения
Пр. Найти циркуляцию векторного поля = yi – x j + z k вдоль окружности

x = r cos t , y = r sin t , z = 1 в положительном направлении, т.е. 0 Непрерывность ФНП

Пусть U=f(M) определена D и в предельной т. M0

Функции U=f(M) называется непрерывной в точке Mo, если выполняются условия:

1) U=f(M) определена в т.M0 и некоторой ее окрестности

2)

3)

18) Свойства ФНП, непрерывной в точке (без док.) (×)

Функции нескольких переменных на замкнутых множествах обладают свойствами аналогичными свойствам функций одной переменной на отрезке.

Свойства непрерывных функций.

Сумма, разность и произведение двух непрерывных функций является непрерывной функцией.

(сумма, разность, произведение непрерывных функций есть непрерывные функции)

2. , ,

-(частное непрерывная функция есть непрерывная фу-я если )

3. -непрерывная функция

4. Основные функции нескольких переменных являются непрерывными всюду на своей области определения.

5. Все функции нескольких переменных являются непрерывными в своей области определения.

Источник

Примеры решения задач по математике

Пример 5. Вычислить циркуляцию векторного поля по контуру l, образованному пересечением поверхностей и . Проверить результат с помощью формулы Стокса.

▲ Пересечением указанных поверхностей (см. пример 4) является окружность . Направление обхода контура выбираем так, чтобы ограниченная им область G (круг) оставалась слева. Запишем параметрические уравнения контура (окружности) . По формулам (9.20) и (9.15) получаем

Применим теперь формулу Стокса (9.21). При возрастании параметра t от 0 до 2 p движение по окружности происходит против часовой стрелки относительно единичного вектора . Ротор данного векторного поля находим по формуле (9.18)

Скалярное произведение вектора на вектор

Поэтому искомая циркуляция (9.21)

что совпадает со значением циркуляции, полученным непосредственным вычислением.

Вопросы для самопроверки

1. Что такое интегральная сумма?

2. Что называется двойным интегралом от функции по области X? Укажите его геометрический смысл.

3. Сформулируйте теоремы о двойном интеграле от суммы и вынесении постоянного множителя за знак двойного интеграла.

4. Напишите формулы, выражающие линейность и аддитивность двойных интегралов.

5. Сформулируйте теорему о формуле среднего значения для двойного интеграла, аналогичную теореме для определенного интеграла.

6. Что называется повторным интегралом от функции по области X? Как он вычисляется?

7. Сведите двойной интеграл к повторному интегралу двумя способами, если G − круг, ограниченный окружностью

8. Что называется тройным интегралом от функции по пространственной области ?

9. Что называется трехкратным интегралом от функции по области V? Как он вычисляется?

10. Напишите формулы, выражающие линейность и аддитивность тройных интегралов.

11. Сформулируйте теорему о среднем для тройного интеграла.

12. Сформулируйте определения: а) интегральных сумм для криволинейного интеграла 1-го рода; б) предела интегральных сумм.

13. Что называется криволинейным интегралом по координатам? Сформулируйте известные вам свойства криволинейного интеграла.

14. Сформулируйте определения: а) интегральных сумм для криволинейного интеграла 2-го рода; б) предела интегральных сумм.

Читайте также: Top secret биокератиновый гель для волос способ применения
15. Что называется криволинейным интегралом по длине дуги плоской кривой?

16. Как вычисляется криволинейный интеграл по кривой, заданной уравнением ?

17. Какое направление обхода замкнутой кривой принимают за положительное направление?

18. Каков смысл обозначения ?

19. Сформулируйте теорему о связи между криволинейными интегралами 1-го и 2-го рода.

20. Сформулируйте свойства линейности и аддитивности криволинейных интегралов 2-го рода.

21. Напишите формулу Грина и сформулируйте условия, при которых она верна.

22. Выведите формулу для вычисления площади плоской фигуры с помощью криволинейного интеграла.

23. Что означает утверждение: «Криволинейный интеграл не зависит от пути интегрирования»?

24. Что означает утверждение: «Выражение является полным дифференциалом в области G?

25. Дайте определение односвязной области на плоскости.

26. Что называется поверхностным интегралом? Напишите формулы для его вычисления.

27. Сформулируйте понятие векторного поля.

28. Дайте определение поверхности: а) двусторонней; б) односторонней; в) ориентированной.

29. Каким характеристическим свойством обладает, двустороння поверхность; односторонняя поверхность?

30. Зависят ли от ориентации поверхности: а) поверхностный интеграл 1-го рода и его интегральные суммы; б) поверхностный интеграл 2-го рода?

31. Как вводится положительное направление обхода контура, согласованное с ориентацией поверхности, ограниченной этим контуром?

32. Напишите формулу Стокса и сформулируйте условия, при которых эта формула верна.

33. Напишите формулу Остроградского-Гаусса и сформулируйте условия, при которых эта формула справедлива.

34. Дайте определение скалярного и векторного полей и приведите примеры физических полей.

35. Что такое поверхности уровня?

36. Что такое векторные линии?

37. Дайте определение производной по направлению для скалярного и векторного полей. Как связана производная по направлению с частными производными?

38. Найдите производную скалярного поля в точке по направлению: а) оси Ox; б) оси Oy; в) вектора l = <1; 1; 1>.

39. Дайте определение градиента скалярного поля. Как связана производная по направлению l с градиентом скалярного поля в данной точке?

40. Какое векторное поле называется потенциальным?

41. Дайте определение дивергенции векторного поля. Каков физический смысл дивергенции?

42. Что называется потоком векторного поля?

43. Дайте определение ротора векторного поля. Каков физический смысл ротора?

44. Какое векторное поле называется безвихревым?

45. Какое векторное поле называется соленоидальным?

46. Что такое оператор Гамильтона?

47. Запишите с помощью оператора Гамильтона: а) градиент скалярного поля; б) дивергенцию векторного поля; в) ротор векторного поля; г) формулу для производной скалярного поля по направлению l.

48. Используя правила вычислений с оператором Гамильтона, докажите, что .

49. Что такое полная производная; локальная производная? Что они характеризуют и каким соотношением связаны?

После изучения тем ”Общая схема построения интегралов. Теория поля“ выполните контрольную работу 9.

Источник