- Определитель матрицы: алгоритм и примеры вычисления определителя матрицы
- Определитель матрицы 3-го порядка: правило треугольника
- Правило Саррюса
- Методы разложения по элементам строки и столбца
- Свойства определителя
- Онлайн калькулятор. Определитель матрицы. Детерминант матрицы.
- Найти определитель (детерминант) матрицы
- Ввод данных в калькулятор для вычисления определителя (детерминанта) матриц
- Дополнительные возможности калькулятора для вычисления определителя (детерминанта) матриц
- Теория. Определитель (детерминант) матрицы.
- Вычисление определителя матрицы 2×2
- Правило треугольника для вычисления определителя матрицы 3×3
- Вычисление определителя матрицы произвольного размера
- Методы вычисления определителей
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Приведение определителя к треугольному виду
- Теорема Лапласа
- Определитель матрицы онлайн
- Предупреждение
- Примеры вычисления определителя матрицы
Определитель матрицы: алгоритм и примеры вычисления определителя матрицы
Определитель (детерминант) матрицы — некоторое число, с которым можно сопоставить любую квадратную матрицу А = ( a i j ) n × n .
|А|, ∆ , det A — символы, которыми обозначают определитель матрицы.
Способ вычисления определителя выбирают в зависимости от порядка матрицы.
Определитель матрицы 2-го порядка вычисляют по формуле:
d e t A = 1 — 2 3 1 = 1 × 1 — 3 × ( — 2 ) = 1 + 6 = 7
Определитель матрицы 3-го порядка: правило треугольника
Чтобы найти определитель матрицы 3-го порядка, необходимо одно из правил:
- правило треугольника;
- правило Саррюса.
Как найти определитель матрицы 3-го порядка по методу треугольника?
а 11 а 12 а 13 а 21 а 22 а 23 а 31 а 32 а 33 = a 11 × a 22 × a 33 + a 31 × a 12 × a 23 + a 21 × a 32 × a 13 — a 31 × a 22 × a 13 — a 21 × a 12 × a 33 — a 11 × a 23 × a 32
А = 1 3 4 0 2 1 1 5 — 1
d e t A = 1 3 4 0 2 1 1 5 — 1 = 1 × 2 × ( — 2 ) + 1 × 3 × 1 + 4 × 0 × 5 — 1 × 2 × 4 — 0 × 3 × ( — 1 ) — 5 × 1 × 1 = ( — 2 ) + 3 + 0 — 8 — 0 — 5 = — 12
Правило Саррюса
Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:
- дописать слева от определителя два первых столбца;
- перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
- перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».
а 11 а 12 а 13 а 21 а 22 а 23 а 31 а 32 а 33 = a 11 × a 22 × a 33 + a 31 × a 12 × a 23 + a 21 × a 32 × a 13 — a 31 × a 22 × a 13 — a 21 × a 12 × a 33 — a 11 × a 23 × a 32
А = 1 3 4 0 2 1 — 2 5 — 1 1 3 0 2 — 2 5 = 1 × 2 × ( — 1 ) + 3 × 1 × ( — 2 ) + 4 × 0 × 5 — 4 × 2 × ( — 2 ) — 1 × 1 × 5 — 3 × 0 × ( — 1 ) = — 2 — 6 + 0 + 16 — 5 — 0 = 3
Методы разложения по элементам строки и столбца
Чтобы вычислить определитель матрицу 4-го порядка, можно воспользоваться одним из 2-х способов:
- разложением по элементам строки;
- разложением по элементам столбца.
Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.
Разложение матрицы по элементам строки:
d e t A = a i 1 × A i 1 + a i 2 × A i 2 + . . . + а i n × А i n
Разложение матрицы по элементам столбца:
d e t A = а 1 i × А 1 i + а 2 i × А 2 i + . . . + а n i × А n i
Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.
А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0
- раскладываем по 2-ой строке:
А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0 = 2 × ( — 1 ) 3 × 1 — 1 3 — 2 5 1 3 1 0 = — 2 × 1 — 1 3 4 5 1 2 1 0 + 1 × 0 — 1 3 — 2 5 1 3 1 0
- раскладываем по 4-му столбцу:
А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0 = 3 × ( — 1 ) 5 × 2 1 0 — 2 4 5 3 2 1 + 1 × ( — 1 ) 7 × 0 1 — 1 2 1 0 3 2 1 = — 3 × 2 1 0 — 2 4 5 3 2 1 — 1 × 0 1 — 1 2 1 0 3 2 1
Свойства определителя
- если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
- если поменять местами строки и столбцы, то знак поменяется на противоположный;
- определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.
Пример 6
А = 1 3 4 0 2 1 0 0 5
d e t А = 1 3 4 0 2 1 0 0 5 = 1 × 5 × 2 = 10
Определитель матрицы, который содержит нулевой столбец, равняется нулю.
Источник
Онлайн калькулятор. Определитель матрицы. Детерминант матрицы.
Используя этот онлайн калькулятор для вычисления определителя (детерминанта) матриц, вы сможете очень просто и быстро найти определитель (детерминант) матрицы.
Воспользовавшись онлайн калькулятором для вычисления определителя (детерминанта) матриц, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на транспонирование матриц, а также закрепить пройденный материал.
Найти определитель (детерминант) матрицы
Введите значения Матрицы:
Ввод данных в калькулятор для вычисления определителя (детерминанта) матриц
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления определителя (детерминанта) матриц
- Между полями для ввода можно перемещаться нажимая клавиши , , и на клавиатуре.
Теория. Определитель (детерминант) матрицы.
Вычисление определителя матрицы 2×2
Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:
| ∆ = |
| = a 11· a 22 — a 12· a 21 |
Правило треугольника для вычисления определителя матрицы 3×3
Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
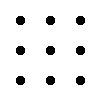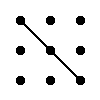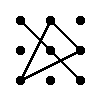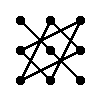 | 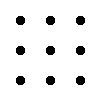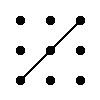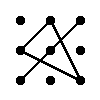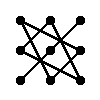 |
| + | – |
| ∆ = |
| = |
Вычисление определителя матрицы произвольного размера
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Источник
Методы вычисления определителей
В общем случае правило вычисления определителей $n$-го порядка является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы 
Задание. Вычислить определитель второго порядка $\left| \begin
Решение. $\left| \begin
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
Методы вычисления определителей не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Вычислить определитель $\left| \begin
Решение. $\left| \begin
$$+3 \cdot 3 \cdot 1-(-1) \cdot 1 \cdot 1-3 \cdot(-2) \cdot 3-4 \cdot 3 \cdot(-2)=54$$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:
Задание. Вычислить определитель $\left| \begin
Решение.
$$+(-1) \cdot 4 \cdot(-2)-(-1) \cdot 1 \cdot 1-3 \cdot 3 \cdot(-2)-3 \cdot 4 \cdot(-2)=54$$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Задание. Разложив по первой строке, вычислить определитель $\left| \begin
Решение. $\left| \begin
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Задание. Вычислить определитель $\left| \begin
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Задание. Вычислить определитель $\left| \begin
Решение. Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих, от второй — пять третьих и от четвертой — три третьих строки, получаем:
Полученный определитель разложим по элементам первого столбца:
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
$$=4 \cdot(2 \cdot 8-4 \cdot 4)=0$$
Последний и предпоследний определители можно было бы и не вычислять, а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.
Задание. Вычислить определитель $\Delta=\left| \begin
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент $a_<11>$ будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
Далее получим нули в первом столбце, кроме элемента $a_<11>$ , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен $\pm 1$ , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:
Ответ. $\Delta=-80$
Теорема Лапласа
Пусть $\Delta$ — определитель $n$-го порядка. Выберем в нем произвольные $k$ строк (или столбцов), причем $k \leq n-1$ . Тогда сумма произведений всех миноров $k$-го порядка, которые содержатся в выбранных $k$ строках (столбцах), на их алгебраические дополнения равна определителю.
Задание. Используя теорему Лапласа, вычислить определитель $\left| \begin
Решение. Выберем в данном определителе пятого порядка две строки — вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
Источник
Определитель матрицы онлайн
Данный онлайн калькулятор вычисляет определитель матрицы. Дается подробное решение. Для вычисления определителя матрицы выбирайте порядок (размер) квадратной матрицы. Введите данные в ячейки. Выберите метод решения и нажмите на кнопку «Вычислить». Теоретическую часть смотрите на странице определитель матрицы.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Примеры вычисления определителя матрицы
Пример 1. Найти определитель матрицы
 . . |
Для вычисления определителя матрицы, приведем матрицу к верхнему треугольному виду.
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого меняем местами строки 1 и 2. При этом меняется знак определителя на «−»:
 . . |
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/78,-2/78 соответственно:
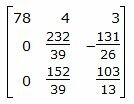 . . |
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -5928/9048:
 . . |
Мы привели матрицу к верхнему треугольному виду. Определитель матрицы равен произведению всех элементов главной диагонали (учитывая знак определителя):
 . . |
Пример 2. Найти определитель матрицы A, разложением определителя по первой строке:
 . . |
Для вычисления определителя матрицы методом разложения по первой строке, вычисляем произведение каждого элемента первой строки на соответствующее алгебраическое дополнение и суммируем полученные результаты:
Источник







