Вычислить двумя способами интеграл задачи 3822

Берман Г.Н. — Сборник задач по курсу математического анализа, страница 40

Описание файла

Просмотр DJVU-файла онлайн

Распознанный текст из DJVU-файла, 40 — страница

(4,4, 41 3820. к44х+У4ГР+ххх вдоль прямой линии. О,1, П р’х4+у4+х4 — х — у+2х 3821. )у’4(х+гз4(у+х*4(г, где 4.— линия пересечения сферы ха+уз+ЕЕ=)тз и цилиндра хз+уз=)тх ()т )О, г

О), обходимая при интегрировании против часовой стрелки, если смотреть нз начала координат. Формула Грина В задачах 3822 †38 криволинейные интегралы по замкнутым контурам Ь, взятые в положительном направлении, преобразовать в двойные интегралы по областям, ограниченным этими контурами. 3822.

(1 — х’) у 4(х+ х (1+ у’) 4(у. 3623. ) (Ехт+ 2х соз у) 4(х+ (ехх — хх ып у) 4(у. 3624. Вычислить двумя способами интеграл задачи 3822, если контуром интегрирования А. служит окружность хх+уз=я’: 1) непосредственно, 2) с помощью формулы Грина. 3823. Вычислить )(ху+х+у)4(х+(ху+х — у) 4(у, где А’.: 1) эллипс —, + —, = 1; 2) окружность х’+ уз = ах. Интегрирование ведется в положительном направлении.

(Вычисление провести двумя способами: 1) непосредственно, 2) с помощью формулы Грина.) гл. хнп квиволинаиныа интагвалы 3626. Доказать, что интеграл ) (ух’+ ет) Их+ (ху’+ хех — 2у) с1у равен нулю. если Š— замкнутая линия, симметричная относительно начала координат. 3827. С помощью формулы Грина вычислить разность между интегралами 1

(х+ у)’ бх — (х — у)’ Иу АмВ ,(2 — ) (х+ у)й гЬ вЂ” (х — у)3 бу, Алв где Ат — отрезок прямой, соединяющей точки А (О, О) и В (1, 1), а А В — дуга параболы у = х’. 3828, Показать, что интеграл ) (хсоз(М, х)+уз(п(У, х)) бз, с где (М, х) — угол между внешней нормалью к линии и положительным направлением оси абсцисс, взятый по замкнутому контуру Е в положительном направлении, равен удвоенной площади фигуры, ограниченной контуром В.

3829. Доказать, что величина интеграла ) (2ху — у

цх+х’ду, с где 1. — замкнутый контур„равна площади области, ограниченной этим контуром. 3830. Доказать, что интеграл

р (у) Их+(хр’ (у)+х'») ду равен с утроенному моменту инерции однородной плоской фигуры, ограниченной контуром 1., относительно оси ординат. Независимость интеграла от контура интегрирования. Отыскание пер во образной В задачах 3831 — 3835 проверить, что интегралы, взятые по замкнутым контурам, равны нулю независимо от вида функций, входящих в подынтегральное выражение. 3831.

(х — у))сЬ+(1(х+у) — 1(х — у))пу. 4 2. КЕИВОЛИНВИНЫВ Интатвалы по Кооелинатам 24! 3835.

(ха+уа+ха) (х ды, составленной плоскостями х=О, д=О, х=О и х+д+ -(-г=1. 3893.

))дг«(х»(д+хг«(дпг+хд»(хдх, где 5 — внешняя сторона поверхности, расположенной в первом октанте и составленной из цилиндра х»+д»=Я» и плоскостей х=О д=О, а=О и г=Н. 3893.

д»гдх«(д+хгдд«(г+х»ддхйг, где 3 — внешняя сторона поверхности, расположенной в первом октанте и составленной пз параболоида вращения г= х’+ д’, цилиндра х’+д’= 1 и координатных плос- а костей (рис. 68). Формула Стокса 3894. Интеграл ) (д’+ а»)«(х+ (х’+ У ь -1-г») с(д+(х»+д») дг, взятый по некоторому замкнутому контуру, преобразовать с помощью формулы Стокса в интеграл по Рис. 68 поверхности, «натянутой» на этот контур. 3895. Вычислить интеграл

х»д»дх+«(д+п(г, где контур Ь вЂ” окружность х’+ д’ = И’, г = О: а) непосредственно н б) используя формулу Стокса, взяв в качестве поверхности полусферу г = +

Интегрирование по окружности в плоскости хОд ведется в положительном направлении. Формула Остроградского 3896. Поверхностный интеграл по замкнутой поверхности преобразовать с помощью формулы Остроградского в тройной гитсграл по обьему тела, ограниченного этой поверхностью;

Источник

Решение двойных интегралов

Калькулятор поможет вычислить двойной интеграл онлайн.
Двойной интеграл представляет собой обобщение понятия определенного интеграла на двумерный случай. Двойным интегралом функции f(x,y) по области D называется предел интегральной суммы lim S (d→0), если он существует. В геометрическом смысле двойной интеграл численно равен объему вертикального цилиндрического тела, построенного на основании и ограниченного сверху соответствующим куском поверхности.

Для получения решения двойных интегралов, нужно ввести необходимые исходные данные в соответствующие ячейки.

Калькулятор поможет решить двойной интеграл онлайн.

• : x^a

• : Sqrt[x]
• : x^(1/n)
• : a^x
• : Log[a, x]
• : Log[x]
• : cos[x] или Cos[x]
• : sin[x] или Sin[x]
• : tan[x] или Tan[x]
• : cot[x] или Cot[x]
• : sec[x] или Sec[x]
• : csc[x] или Csc[x]
• : ArcCos[x]
• : ArcSin[x]
• : ArcTan[x]
• : ArcCot[x]
• : ArcSec[x]
• : ArcCsc[x]
• : cosh[x] или Cosh[x]
• : sinh[x] или Sinh[x]
• : tanh[x] или Tanh[x]
• : coth[x] или Coth[x]
• : sech[x] или Sech[x]
• : csch[x] или Csch[е]
• : ArcCosh[x]
• : ArcSinh[x]
• : ArcTanh[x]
• : ArcCoth[x]
• : ArcSech[x]
• : ArcCsch[x]
• [19.67] =19: integral part of (19.67) — выделяет целую часть числа (integerPart)

Интегралы

Для того, чтобы найти неопределенный интеграл от функции нужно написать в строке: f[x], x. Найти определенный интеграл так же просто: f[x], либо e f(x), x=a..b.

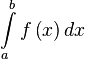
Важно подчеркнуть, что калькулятор выдает пошаговое нахождение интеграла при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.

Источник

Примеры решений двойных интегралов

В этом разделе вы найдете подробные решения заданий с использованием двойных интегралов разной сложности. Для удобства использования примеры разбиты по подразделам:

Порядок интегрирования: примеры решений

Задача 1. Изменить порядок интегрирования.

$$ \int_0^1 dy \int_<-\sqrt>^0 fdx +\int_1^e dy \int_<-1>^<\ln> fdx $$

Задача 2. Свести к однократному интегралу

Задача 3. Изменить порядок интегрирования. Нарисовать область интегрирования и вычислить двойной интеграл двумя способами.

Трудности с задачами? МатБюро поможет с интегралами.

Двойной интеграл по области: примеры решений

Задача 4. Вычислить двойной интеграл по области $D$

Задача 5. Вычислить двойной интеграл от функции $z=x^3+y^3-3xy$ по области D, заданной системой неравенств $0 \le x \le 2$, $y \le \sqrt$. Область D изобразить на рисунке.

Задача 6. Вычислить с помощью перехода к полярным координатам двойной интеграл по указанной области $D$.

Площади: примеры решений

Задача 7. Вычислить площадь области D: $y=-2x^2+2, y \ge -6$.

Задача 8. Найти площадь области $x^2-2x+y^2=0$, $x^2-4x+y^2=0$, $y=0$, $y=\sqrt<3>x$.

Задача 9. С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями (неравенствами) $y=x^2,x=2y^2$

Задача 10. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной заданными линиями.

Задача 11. Вычислить площадь области, заданной неравенствами $(x-r)^2+y^2 \le r^2, y \ge 0, -2x+2r \ge y$, перейдя предварительно к полярным координатам.

Если вам нужна помощь в нахождении интегралов, выполнении домашней работы или типовика по интегральному исчислению, будем рады принять ваш заказ на решение. Стоимость от 60 рублей, срок от нескольких часов.

Объемы: примеры решений

Задача 12. Найти объем тела, заданного ограничивающими его поверхностями.

$$ x^2+y^2=2y, \quad x^2+y^2=5y, \quad z=\sqrt, \quad z=0. $$

Задача 13. С помощью двойного интеграла вычислить объем тела, ограниченного поверхностями

$$ a^2 \le x^2+y^2 \le b^2, \quad x^2-y^2-z^2 \ge 0, x\ge 0$$

Задача 14. Вычислить объем тела, ограниченного поверхностями, с помощью двойного и тройного интеграла $x^2+y^2=4x,x^2+y^2+z^2=16$

Масса, центр тяжести, момент: примеры решений

Задача 15. Пластина $D$ задана уравнениями $x=1$, $y \ge 0$, $y^2=4x$ с плотностью $\mu = 6x+3y^2$. Найти массу пластины.

Задача 16. Найти координаты центра тяжести однородной пластины, ограниченной кривой

$$ x=a(t-\sin t), y=a(1-\cos t), \quad 0 \le t \le 2\pi; y=0. $$

Задача 17. Найти центр тяжести плоской пластины, ограниченной кривой $(x+y)^4=xy$, имеющей плотность

Задача 18. Используя двойной интеграл, вычислить статический момент относительно оси $Ox$ тонкой однородной пластинки, имеющей форму области $D$, ограниченной заданными линиями. Построить чертеж области интегрирования

Задача 19. Найти массу круглой пластины $D: x^2+y^2 \le 1$ с поверхностной плотностью $\rho(x,y)=3-x-y$.

Задача 20. Найти момент инерции относительно оси $Ox$ однородной фигуры, ограниченной двумя кривыми $y^2=8x+4$, $y^2=-8x+4$.

Источник

Неопределенный интеграл

Неопределенный интеграл онлайн

В школе говорят, интеграл – это значок ∫, а вычисление интеграла, то есть процесс интегрирования, – это операция обратная дифференцированию. Согласитесь скучно!

Разумеется, у школьников возникает резонный вопрос: а нафиг он нам нужен?

Но если бы учитель уделил несколько минут на вводную про интегралы, такой вопрос всё равно бы возник, но уже не у всех!

Вводная к интегралам

В далеком 17 веке были на тот момент нерешенные насущные проблемы, а именно изучались закономерности движения тел. Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.

Допустим, мы знаем закон изменения скорости тела – это некая функция. Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.

В этом заключается один из физических смыслов интеграла.

Как вы уже поняли, геометрический смысл интеграла – это площадь криволинейной трапеции. Соответственно с помощью кратного интеграла вычисляется объем тела.

Лейбниц и Ньютон заложили основы дифференциального и интегрального исчисления. В последующие десятилетия было много великих открытий, связанных с вычислением интегралов.

Поскольку подынтегральная функция может принимать различные виды, естественно это привело к разделению интегралов на свои типы, а главное были отрыты многочисленные методы решения интегралов.

Но не все так безоблачно. На практике часто происходит так, что в аналитическом виде вычислить интегралы невозможно, то есть используя какой-либо известный метод. Конечно, получить аналитическое решение это здорово, но, с другой стороны, главное ведь вычислить точное значение интеграла. В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.

Калькулятор решения интегралов

Теперь самое интересное. Еще каких-то 15 лет назад школьник и помыслить не мог, что под рукой будут такие калькуляторы интегралов, как, например, наш. Это безусловно облегчает процесс обучения. Можно проверять свои решения, находить допущенные ошибки и лучше усваивать образовательный курс.

И тут в который раз повторяем, калькулятор решения интегралов – это только ваш безотказный помощник, к которому можете обратиться в любое время. Но никак не подмена вашей головы. Старайтесь самостоятельно решать задачи, только так можно развивать мышление, а компьютер будет в помощь.

Источник

Примеры решений криволинейных интегралов

В этом разделе вы найдете подробные решения криволинейных интегралов первого и второго рода (непосредственное вычисление, по разным путям, по формуле Грина), а также применение к вычислению моментов инерции, массы, работы, силы притяжения и т.п.

Криволинейные интегралы 1-го рода: примеры решений

Задача 1. Вычислить криволинейный интеграл первого рода по указанной кривой $L$:

Задача 2. Вычислить криволинейный интеграл I рода $\int_L y^2 dl$, $L$ — арка циклоиды $x=(t-\sin t)/2$, $y=(1-\cos t)/2$, $0 \le t \le \pi$.

Задача 3. Вычислить криволинейный интеграл $\int_L y^2 dl$, где $L$ – дуга параболы $y^2=2x$ от точки $(0;0)$ до точки $(1;\sqrt<2>)$.

Если вам нужна помощь в нахождении интегралов, выполнении домашней работы, будем рады принять ваш заказ на решение. Стоимость от 100 рублей, срок от нескольких часов.

Криволинейные интегралы 2-го рода: примеры решений

Задача 4. Вычислить криволинейный интеграл второго рода, взятый вдоль ориентированной кривой $L$: $\int_L x^2 dy -xydx$, где $L$ — часть кривой $x^4-y^4=6x^2y$ от точки $A=(-4\sqrt<2>;4)$ до точки $B=(0;0)$

Задача 5. Вычислить интеграл $$\int_L z^2x dx +(z+x+y)dy +y^2zdz,$$ где $L$ — кривая $a^2+y^2=ax, x^+y^2=z^2$ положительно ориентированная на внешней стороне цилиндра.

Задача 6. Вычислить криволинейный интеграл $\int_ (y^2+x)dx+2x/y dy$ вдоль кривой $y=e^x$ от точки $A(0;1)$ до точки $B(1;e)$.

Задача 7. Проверить, что криволинейный интеграл не зависит от пути интегрирования и найти его значение.

Задача 8. Проверить криволинейный интеграл, который не зависит от пути интегрирования, и найти его значение (двумя способами – непосредственно и с помощью потенциала).

Задача 9. Вычислить криволинейный интеграл по замкнутому контуру в положительном направлении, используя формулу Грина

$$\int_l (x-y^2)dy + (x^3+3y)dx, \quad l: x=y, y=x^2.$$

Трудности с задачами? МатБюро поможет с интегралами.

Моменты инерции: примеры решений

Задача 10. Найти моменты инерции относительно осей однородных дуг $L$ плотности $\rho$.

Задача 11. Вычислить момент инерции верхней половины окружности $x^2+y^2=a^2$ относительно оси $Oy$, если плотность $\delta=1$.

Другие задания: примеры решений

Задача 12. Найти координаты силы притяжения дугой астроиды $x=a \cos^3 t$, $y=a \sin^3 t$, $0 \le t \le \pi/2$ единичной массы, помещенной в начале координат, если плотность астроиды в каждой ее точке равна кубу расстояния этой точки от начала координат.

Задача 13. Вычислить работу силы $F(z,-x,y)$ вдоль дуги винтовой линии $z=2\cos t$, $y=3\sin t$, $z=4t$, $0 \le t \le 2\pi$.

Задача 14. Доказать, что данное выражение $P(x,y)dx+Q(x,y)dy$ является полным дифференциалом функции $Ф(x,y)$ и найти ее с помощью криволинейного интеграла.

Задача 15. Вычислить работу силы $\overline$ при перемещении точки приложения силы вдоль заданной кривой $L$ от точки $B$ до точки $C$, если значения параметра $t$ в точках $B$ и $C$ заданы.

$$ \overline=-x \overline+2y^2\overline, \quad x=2\cos t, y=\sint, \quad t_B=0, t_C=\pi/6. $$

Задача 16. Вычислить массу кривой $y=x^2/2$, где $x\in (\sqrt<3>, 2\sqrt<2>)$, если линейная плотность задана функцией $f(x,y)=6y/x$.

Источник