Вычисление объема пирамиды разными способами

Нахождение объема пирамиды: формула и задачи

В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.

Формула вычисления объема пирамиды

1. Общая формула

Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.

• ABCD – основание;
• E – вершина;
• h – высота, перпендикулярная основанию.

2. Объем правильной треугольной пирамиды

Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):

Подставляем данное выражение в формулу расчета объема фигуры и получаем:

3. Объем правильной четырехугольной пирамиды

Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a 2 , где а – длина его стороны.

Следовательно, формулу объема можно представить в виде:

4. Объем правильной шестиугольной пирамиды

Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):

С учетом этого, объем фигуры считается так:

Примеры задач

Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:

Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.

Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см 2 (3 см ⋅ 3 см). Следовательно, объем равен:

Источник

Объемы фигур. Объем пирамиды.

Пирамида — это многогранник, у которого одна грань — основание пирамиды — произвольный многоугольник, а остальные — боковые грани — треугольники с общей вершиной, называемой вершиной пирамиды.

По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д. Пирамида является частным случаем конуса.

Воспользуйтесь онлайн калькулятором для расчета объема пирамиды: объем пирамиды, онлайн расчет.

Для расчета объемов других тел воспользуйтесь этим калькулятором: калькулятор объемов фигур.

Элементы пирамиды.

• апофема — высота боковой грани правильной пирамиды, проведённая из её вершины (также апофемой называют длину перпендикуляра, опущенного из середины правильного многоугольника на одну из его сторон);
• боковые грани — треугольники, сходящиеся в вершине;
• боковые ребра — общие стороны боковых граней;

• вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;

• высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра);
• диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;
• основание — многоугольник, которому не принадлежит вершина пирамиды.

Вспомогательные формулы.

1. Боковая поверхность — это сумма площадей боковых граней:

2. Полная поверхность — это сумма площади боковой поверхности и площади основания:

3. Боковая поверхность — это сумма площадей боковых граней:

P — периметр основания,

n — число сторон основания,

b — боковое ребро,

α — плоский угол при вершине пирамиды.

Общая формула, по которой можно найти объем пирамиды.

Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS)

, где

S – площадь основания пирамиды,

h – высота пирамиды

— объём параллелепипеда;

Правильная пирамида.

Правильная пирамида — пирамида, в основании, которой лежит правильный многоугольник, а высота проходит через центр вписанной окружности в основание.

Формула для вычисления объема правильной пирамиды:

h — высота пирамиды

a — сторона основания пирамиды

n — количество сторон многоугольника в основании

Правильная треугольная пирамида.

Правильная треугольная пирамида — пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.

Формула для нахождения объема правильной треугольной пирамиды:

h — высота пирамиды

a — сторона основания пирамиды

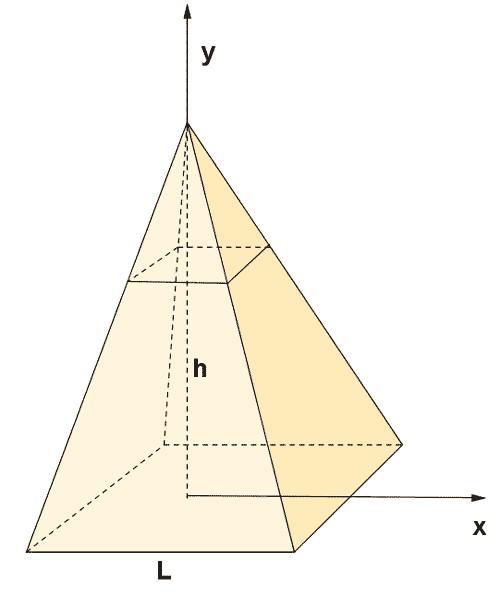
Правильная четырехугольная пирамида.

Правильная четырехугольная пирамида — пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.

Формула для определения объема правильной четырехугольной пирамиды:

h — высота пирамиды

a — сторона основания пирамиды

Тетраэдр.

Тетраэдр — пирамида, у которой все грани — равносторонние треугольники.

Формулы для вычисления объема тетраэдра:

a — ребро тетраэдра

— скрещивающиеся рёбра, — расстояние между a₁ и a₂, — угол между a₁ и a₂;

Усеченная пирамида.

Сечение параллельное основанию пирамиды делит пирамиду на две части. Часть пирамиды между ее основанием и этим сечением — это усеченная пирамида.

Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S₁ (abcde), нижнего основания усеченной пирамиды S₂ (ABCDE) и средней пропорциональной между ними.

S₁ — площадь верхнего основания усеченной пирамиды,

S₂ — площадь нижнего основания усеченной пирамиды,

Источник

Формулы объема пирамиды полной и усеченной. Объем пирамиды Хеопса

Умение вычислять объем пространственных фигур является важным при решение ряда практических задач по геометрии. Одной из распространенных фигур является пирамида. В данной статье рассмотрим формулы объема пирамиды как полной, так и усеченной.

Пирамида как объемная фигура

Каждый знает о египетских пирамидах, поэтому хорошо представляет, о какой фигуре пойдет речь. Тем не менее египетские каменные сооружения являются лишь частным случаем огромного класса пирамид.

Рассматриваемый геометрический объект в общем случае представляет собой многоугольное основание, каждая вершина которого соединена с некоторой точкой в пространстве, не принадлежащей плоскости основания. Данное определение приводит к фигуре, состоящей из одного n-угольника и n треугольников.

Вам будет интересно: Балбес – это кто? Сказка и реальность

Любая пирамида состоит из n+1 граней, 2*n ребер и n+1 вершины. Поскольку рассматриваемая фигура является совершенным полиэдром, то числа отмеченных элементов подчиняются равенству Эйлера:

Многоугольник, находящийся в основании, дает название пирамиды, например, треугольная, пятиугольная и так далее. Набор пирамид с разными основаниями приведен на фото ниже.

Точка, в которой n треугольников фигуры соединяются, называется вершиной пирамиды. Если из нее опустить на основание перпендикуляр и он пересечет его в геометрическом центре, тогда такая фигура будет называться прямой. Если это условие не выполняется, то имеет место наклонная пирамида.

Прямая фигура, основание которой образовано равносторонним (равноугольным) n-угольником, называется правильной.

Формула объема пирамиды

Для вычисления объема пирамиды воспользуемся интегральным исчислением. Для этого разобьем фигуру параллельными основанию секущими плоскостями на бесконечное число тонких слоев. Рисунок ниже показывает четырехугольную пирамиду высотой h и длиной стороны L, в которой четырехугольником отмечен тонкий слой сечения.

Площадь каждого такого слоя можно вычислить по формуле:

Здесь A0 — площадь основания, z — значение вертикальной координаты. Видно, что если z = 0, то формула дает значение A0.

Чтобы получить формулу объема пирамиды, следует вычислить интеграл по всей высоте фигуры, то есть:

Подставляя зависимость A(z) и вычисляя первообразную, приходим к выражению:

V = -A0*(h-z)3/(3*h2)|h0 = 1/3*A0*h.

Мы получили формулу объема пирамиды. Чтобы найти величину V, достаточно умножить высоту фигуры на площадь основания, а затем результат поделить на три.

Заметим, что полученное выражение справедливо для вычисления объема пирамиды произвольного типа. То есть она может быть наклонной, а ее основание представлять собой произвольный n-угольник.

Правильная пирамида и ее объем

Полученную в пункте выше общую формулу для объема можно уточнить в случае пирамиды с правильным основанием. Площадь такого основания вычисляется по следующей формуле:

Здесь L является длиной стороны правильного многоугольника с n вершинами. Символ pi — это число пи.

Подставляя выражение для A0 в общую формулу, получаем объем правильной пирамиды:

Vn = 1/3*n/4*L2*h*ctg(pi/n) = n/12*L2*h*ctg(pi/n).

Например, для треугольной пирамиды эта формула приводит к следующему выражению:

V3 = 3/12*L2*h*ctg(60o) = √3/12*L2*h.

Для правильной четырехугольной пирамиды формула объема приобретает вид:

V4 = 4/12*L2*h*ctg(45o) = 1/3*L2*h.

Определение объемов правильных пирамид требует знания стороны их основания и высоты фигуры.

Пирамида усеченная

Предположим, что мы взяли произвольную пирамиду и отсекли у нее часть боковой поверхности, содержащей вершину. Оставшаяся фигура называется усеченной пирамидой. Она состоит уже из двух n-угольных оснований и n трапеций, которые их соединяют. Если секущая плоскость была параллельна основанию фигуры, тогда образуется усеченная пирамида с параллельными подобными основаниями. То есть длины сторон одного из них можно получить, умножая длины другого на некоторый коэффициент k.

Рисунок выше демонстрирует усеченную правильную шестиугольную пирамиду. Видно, что верхнее основание ее так же, как и нижнее, образовано правильным шестиугольником.

Формула объема усеченной пирамиды, которую можно вывести, используя подобное приведенному интегральное исчисление, имеет вид:

V = 1/3*h*(A0 + A1 + √(A0*A1)).

Где A0 и A1 — площади нижнего (большого) и верхнего (маленького) оснований соответственно. Переменной h обозначается высота усеченной пирамиды.

Объем пирамиды Хеопса

Любопытно решить задачу на определение объема, который заключает внутри себя самая большая египетская пирамида.

В 1984 году британские египтологи Марк Легнер (Mark Lehner) и Джон Гудман (Jon Goodman) установили точные размеры пирамиды Хеопса. Ее первоначальная высота равнялась 146,50 метра (в настоящее время около 137 метров). Средняя длина каждой из четырех сторон сооружения составила 230,363 метра. Основание пирамиды с высокой точностью является квадратным.

Воспользуемся приведенными цифрами для определения объема этого каменного гиганта. Поскольку пирамида является правильной четырехугольной, тогда для нее справедлива формула:

Подставляем цифры, получаем:

V4 = 1/3*(230,363)2*146,5 ≈ 2591444 м3.

Объем пирамиды Хеопса равен практически 2,6 млн м3. Для сравнения отметим, что олимпийский бассейн имеет объем 2,5 тыс. м3. То есть для заполнения всей пирамиды Хеопса понадобится больше 1000 таких бассейнов!

Источник