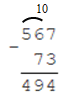Вычесть удобным способом 5 класс

Основные правила и свойства вычитания для 5 класса

Учащиеся средних образовательных школ изучают в 5 классе свойства вычитания и сложения. Они применяются для решения примеров, ускорения вычислений в устной форме и т. д. В высших учебных заведениях правила используются для упрощения выражений, нахождения корней дифференциальных уравнений и пределов, а также для выполнения других операций.

Общая информация

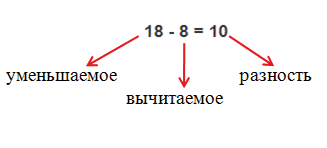
Вычитание — операция уменьшения числа на определенное значение. Для примера следует записать следующее выражение: p — t = v. Первая величина называется уменьшаемым, вторая — вычитаемым, а результат вычитания — разность. Очень часто в литературе с физико-математическим уклоном можно встретить связку «разность двух чисел», которая является синонимом вычитания.

Сложение — математическая операция, применяемая для увеличения числа на некоторое значение. Коэффициенты имеют такие названия (p + t = v):

1. p — первое слагаемое.
2. t — второе слагаемое.
3. v — сумма.

Формулировка сочетательного закона сложения следующая: чтобы прибавить к сумме двух чисел, сгруппированных в скобках, третью величину, необходимо осуществить операцию сложения первого и третьего, а затем к результату прибавить второе слагаемое. В буквенном виде он записывается в таком виде: (t + v) + s = (t + s) + v. Справедлива будет и такая запись: (t + v) + s = (v + s) + t. Переместительный и сочетательный законы позволяют группировать слагаемые в любой последовательности.

Методы вычитания

Для выполнения операции разности чисел нужно придерживаться определенных свойств вычитания. В 5 классе изучаются все необходимые формулы и утверждения, к которым можно отнести следующие:

1. При вычитании 0 из числа получается искомое число: t — 0 = t.
2. Если из нулевого значения вычесть число, результат будет эквивалентен величине, взятой со знаком «- «: т. е. 0 — t = -t.
3. Разность двух чисел, эквивалентных между собой, соответствует нулевой величине: t — t = 0.
4. Для вычитания суммы двух слагаемых из числа нужно из последнего вычесть первое слагаемое, а затем второе: t — (s + v) = t — s — v.
5. Чтобы вычислить разность суммы двух слагаемых и вычитаемого, нужно отнять из первого слагаемого вычитаемое, а затем к результату прибавить II слагаемое: (t + s) — v = t — v + s.
6. Если одним из слагаемых является разность двух чисел (составное), необходимо к первому значению прибавить уменьшаемое, а затем из результата вычесть вычитаемое: t + (s — v) = t + s — v.

В шестом законе вычитания для 5 класса требуется просто раскрыть скобки без изменения знаков величин. Специалисты рекомендуют записать все правила в специальные таблицы-тренажеры, которые должны всегда быть под рукой.

Таким образом, для выполнения арифметических операций сложения и вычитания нужно знать все основные свойства и формулы, позволяющие оптимизировать вычисления.

Источник

Вычитание натуральных чисел

Понятие «вычитание»

Вычитание — одно из четырех арифметических действий. Вычитание записывают при помощи знака «-» минус.

Например: 34 — 13 = 21

Вычитание — действие обратное сложению.

То есть, 25 — 6 = 19 ⇔ 19 + 6 = 25

Обозначения

Число из которого вычитают, называется уменьшаемым. 18 — уменьшаемое.

Число, которое вычитают, называется вычитаемым. 8 — вычитаемое.

Результат вычитания, называется разностью. 10 — разность.

Свойства вычитания натуральных чисел

1) При вычитании натуральных чисел уменьшаемое всегда должно быть больше вычитаемого.

100 — 60 = 40 100 — 101 = не натуральное число

2) Разность показывает на сколько больше уменьшаемое больше вычитаемого.

34 больше, чем 7 на 17 единиц.

3) Если вычитаемое равно 0, разность равна уменьшаемому.

4) Если от любого числа вычесть 1, то получим число предшествующее данному.

5) Вычитание натурального числа из суммы натуральных чисел.

Чтобы вычесть натуральное число из суммы натуральных чисел, необходимо сначала сложить числа, а затем вычесть данное натуральное число, или первым действием вычесть данное натуральное число из любого слагаемого, а к разности прибавить оставшееся слагаемое.

(26 + 9) — 6 = 26 — 6 + 9

6) Вычитание суммы чисел из натурального числа.

Чтобы вычесть сумму чисел из натурального числа, необходимо сначала сложить два числа, после этого вычесть полученную сумму из данного числа, или вычесть из данного числа любое из слагаемых, поле этого вычесть второе.

47 — (16 + 7) = 47 — 7 — 16

Вычитание чисел с разными разрядами

Для того чтобы вычесть числа с разным разрядом, необходимо разложить числа по разрядам.

567 = 500 + 60 + 7 = 400 + 100 + 60 + 7

Из единиц вычтем единицы, из десятков десятки, из сотен сотни и т.д.

7 — 3 = 4;

Поскольку из 60 нельзя вычесть 70, разложим 500 на 400 и 100, прибавим 100 к 60

(100 + 60) — 70 = 90;

400 — 0 = 400.

Полученное число: 400 + 90 + 4 = 494.

Вычитание в столбик

Многозначные числа удобнее всего вычитать в столбик. Для того чтобы вычесть число из числа в столбик, необходимо:

1. Правильно записать числа. Первым записываем уменьшаемое, под уменьшаемым пишем вычитаемое, так чтобы каждый разряд вычитаемого находился строго под соответствующим разрядом вычитаемого. Слева поставим знак «-» под столбиком, состоящим из уменьшаемого и вычитаемого проводим черту

2. Справа налево последовательно вычитаем из разряда уменьшаемого соответствующий разряд вычитаемого. Результат запишем под чертой, это будет разность.

3 Если разряд уменьшаемого окажется меньше разряда вычитаемого занимаем 10 у разряда стоящего слева (см. рисунок).

Вычитание с помощью координатного луча

Для вычитания с помощью координатного луча, отметим точку соответствующую уменьшаемому, в нашем примере, это число 12. Для вычитания отсчитываем влево количество единичных отрезков равных вычитаемому (8). Получившаяся точка будет являться разницей (4).

Поделись с друзьями в социальных сетях:

Источник

Математика. 5 класс

Конспект урока

Перечень вопросов, рассматриваемых в теме:

— понятие разности двух чисел;

— вычитание натуральных чисел;

— проверка правильности вычитания – сложением;

— свойство прибавления к уменьшаемому и вычитаемому одного и того же числа.

Разность чисел a и b – это такое число, которое при сложении с числом b даёт число а. Число а называют уменьшаемым, число b – вычитаемым.

Чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности – второе слагаемое.

Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое. Стоит помнить, что вычитаемое должно быть не больше слагаемого, из которого его вычитают.

Если к уменьшаемому и вычитаемому одновременно прибавить одно и то же число, то разность от этого не изменится.

1. Никольский С. М. Математика: 5 класс. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2017. – 272 с.
2. Потапов М. К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.

1. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
2. Потапов М. К. Математика: дидактические материалы. 6 класс. // М. К. Потапов, А. В. Шевкин – М.: Просвещение, 2010.- 118 с.
3. Чесноков А. С. Дидактические материалы по математике 5 класс. // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.

Теоретический материал для самостоятельного изучения

Разностью чисел a и bназывают такое число, которое при сложении с числом b даёт число а. Число а называют уменьшаемым, число b – вычитаемым.

Разность чисел а и b обозначают а – b.

Таким образом, (а – b) + b = a или а – b + b = a.

Рассмотрим, как, используя числовую прямую, можно найти разность натуральных чисел а и b в случае, когда a>b.

Пусть нам надо найти разность 8 – 5. Отметим на числовом луче число 8 и отсчитаем от него влево пять делений. Получим число 3.

Мы видим, что сумма 3 и 5 равна 8.

Поэтому число 3 есть разность чисел 8 и 5, то есть 8 – 5 = 3.

Стоит отметить, что для любого числа a верны равенства:

а – 0 = а, потому что а + 0 = а

а – а = 0, потому что 0 + а = а

При действиях с натуральными числами уменьшаемое не может быть меньше вычитаемого.

Разность двух чисел показывает, на сколько первое число больше второго, иными словами, на сколько второе число меньше первого.

Рассмотрим такой пример: 12 – (3 + 4) = 12 – 3 – 4 = 5.

Чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности – второе слагаемое. Это свойство называют свойством вычитания суммы из числа.

Рассмотрим следующее выражение: (6 + 5) – 4 = 6 + 5 – 4 = 7

Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое. Стоит помнить, что вычитаемое должно быть не больше слагаемого, из которого его вычитают. Это свойство называют свойством вычитания числа из суммы.

Найдём разность двух сумм:

(7 + 2) – (4 + 2) = 9 – 6 = 3 или

(7 + 2) – (4 + 2) = 7 + 2 – 4 – 2 = 3.

Это свойство прибавления к уменьшаемому и вычитаемому одного и того же числа: если к уменьшаемому и вычитаемому одновременно прибавить одно и то же число, то разность от этого не изменится, то есть (a + n) – (b + n) = a–b.

Разбор решения заданий тренировочного модуля

№ 1.Чему равно значение выражения: 139 – 42 – 63? Выберите правильный ответ.

Варианты ответов: 34; 97; 90; 134.

Решение: чтобы решить данное выражение, надо вычесть 42 из 139, что даст 97, а затем ещё раз вычесть 63. В итоге получим 34.

№ 2. Путешественник должен пройти 56 км. В первый день он прошёл 27 км. Сколько км ему ещё осталось пройти?

Решение: чтобы узнать сколько километров осталось пройти путешественнику, необходимо из 56 вычесть 27: так получим 29 (км).

Источник

Свойства сложения и вычитания

О чем эта статья:

Свойства сложения

Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число

Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.

Слагаемые — это числа, единицы которых складываются.

Сумма — это число, которое получается в результате сложения.

Рассмотрим пример 2 + 5 = 7, в котором:

• 2 — это первое слагаемое,
• 5 — второе слагаемое,
• 7 — это сумма.

При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.

Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.

1. Переместительное свойство сложения
   От перестановки мест слагаемых сумма не меняется.
   a + b = b + a
2. Сочетательное свойство сложения
   Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.
   (a + b) + c = a + (b + c)
3. Свойство нуля при сложении
   Если к числу прибавить нуль, получится само число.
   a + 0 = 0 + a = a

Свойства вычитания

Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.

Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.

Уменьшаемое — это число, из которого вычитают.

Вычитаемое — это число, которое вычитают.

Разность — это число, которое получается в результате вычитания.

Рассмотрим пример 9 — 4 = 5, в котором:

9 — это уменьшаемое,

4 — вычитаемое,

5 — разность.

При этом саму запись (9 — 4) тоже можно назвать разностью.

1. Свойство нуля при вычитании
   Если из числа вычесть нуль, получится само число.
   a — 0 = a
   Если из числа вычесть само число, то получится нуль.
   a — a = 0
2. Свойство вычитания суммы из числа
   Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое.
   a — (b + c) = a — b — c
3. Свойство вычитания числа из суммы
   Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
   (a + b) — c = (a — c) + b (если a > c или а = с)
   (a + b) — c = (b — c) + a (если b > c или b = с)

Примеры использования свойств сложения и вычитания

Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:

Пример 1

Вычислить сумму слагаемых с использованием разных свойств:

а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15

б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22

в) 30 + 0 + 13 = 30 + 13 = 43

Пример 2

Применить разные свойства при вычислении разности:

а) 25 — 0 — 2 = 25 — 2 = 23

б) 18 — (1 + 4) = 18 — 1 — 4 = 17 — 4 = 13

Пример 3

Найти значение выражения удобным способом:

а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32

б) 16 — (4 + 3) + 7 = 16 — 4 — 3 + 7 = (16 — 4) — 3 + 7 = 12 — 3 + 7 = 9 + 7 = 16

Источник