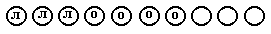Выбрать способ решения задачи

2) 90 — 10 = 50 (к.) на 3 полке.

1) Сколько книг на первой и второй полках вместе?

2) Сколько книг на третьей полке?

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:

90 — (28 + 12) = 50 (к.)

Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.

Например, рассмотренную выше задачу можно решить другим арифметическим способом:

1) 90 — 28 = 62 (к.) на 2 и3 полках.

2) 62 — 12 = 50 (к.) на 3 полке.

В качестве арифметического способа можно рассматривать и такое решение данной задачи:

1) 90 — 12 = 78 (к.) на 2 и 3 полках.

2) 78 -28 = 50 (к.) на З полке.

В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.

Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?

Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:

Ответ: 27 машин было в гараже

Решение задачи можно оформить так:

48 : 3 = 16 (л.) Ответ: 16 листов

[../../../_private/navbar1.htm]

Источник

Как решать логические и математические задачи

Решение задач на логику — отличная гимнастика для ума детей и взрослых на каждый день. На ЛогикЛайк более 3500 заданий с ответами и пояснениями, полноценный учебный комплекс для развития логики и способностей к математике.

Решаем логические задачи

Чтобы научиться решать типовые логические задачи, простые и нестандартные математические задачи, важно знать основные приемы и методы их решения. Ведь решить одну и ту же задачу и прийти к правильному ответу во многих случаях можно разными способами.

Знание и понимание различных методов решения поможет определить, какой способ подойдет лучше в каждом конкретном случае, чтобы выбрать наиболее быстрый и простой путь получения ответа.

К «классическим» логическим задачам относятся текстовые задачи, цель решения которых состоит в распознавании объектов или расположении их в определенном порядке в соответствии с заданными условиями.

Более сложными и увлекательными типами заданий являются задачи, в которых отдельные утверждения являются истинными, а другие ложными. Задачи на перемещение, перекладывание, взвешивание, переливание — самые яркие примеры широкого ряда нестандартных задач на логику.

Основные методы решения логических задач

• метод рассуждений;
• с помощью таблиц истинности;
• метод блок-схем;
• средствами алгебры логики (алгебры высказываний);
• графический (в том числе, «дерево логических условий», метод кругов Эйлера);
• метод математического бильярда.

Давайте рассмотрим подробнее с примерами три популярных способа решения логических задач, которые мы рекомендуем использовать в начальной школе (детям 6-12 лет):

• метод последовательных рассуждений;
• разновидность метода рассуждений — «с конца»;
• табличный способ.

Метод последовательных рассуждений

Самый простой способ решения несложных задач заключается в последовательных рассуждениях с использованием всех известных условий. Выводы из утверждений, являющихся условиями задачи, постепенно приводят к ответу на поставленный вопрос.

На столе лежат Голубой , Зеленый , Коричневый и Оранжевый карандаши.

Третьим лежит карандаш, в имени которого больше всего букв. Голубой карандаш лежит между Коричневым и Оранжевым .

Разложи карандаши в описанном порядке.

Рассуждаем. Последовательно используем условия задачи для формулирования выводов о позиции, на которой должен лежать каждый следующий карандаш.

• Больше всего букв в слове «коричневый», значит, он лежит третьим.
• Известно, что голубой карандаш лежит между коричневым и оранжевым. Справа от коричневого есть только одна позиция, значит, расположить голубой между коричневым и другим карандашом возможно только слева от коричневого.
• Следующий вывод на основе предыдущего: голубой карандаш лежит на второй позиции, а оранжевый — на первой.
• Для зеленого карандаша осталась последняя позиция — он лежит четвертым.

Метод «с конца»

Такой способ решения является разновидностью метода рассуждений и отлично подходит для задач, в которых нам известен результат совершения определенных действий, а вопрос состоит в восстановлении первоначальной картины.

Бабушка испекла для троих внуков рогалики и оставила их на столе. Коля забежал перекусить первым. Сосчитал все рогалики, взял свою долю и убежал.
Аня зашла в дом позже. Она не знала, что Коля уже взял рогалики, сосчитала их и, разделив на троих, взяла свою долю.
Третьим пришел Гена, который тоже разделил остаток выпечки на троих и взял свою долю.
На столе осталось 8 рогаликов.

Сколько рогаликов из восьми оставшихся должен съесть каждый, чтобы в результате все съели поровну?

Начинаем рассуждение «с конца».
Гена оставил для Ани и Коли 8 рогаликов (каждому по 4). Получается, и сам он съел 4 рогалика: 8 + 4 = 12.
Аня оставила для братьев 12 рогаликов (каждому по 6). Значит, и сама она съела 6 штук: 12 + 6 = 18.
Коля оставил ребятам 18 рогаликов. Значит, сам съел 9: 18 + 9 = 27.

Бабушка положила на стол 27 рогаликов, рассчитывая, что каждому достанется по 9 штук. Поскольку Коля уже съел свою долю, Аня должна съесть 3, а Гена — 5 рогаликов.

Решение логических задач с помощью таблиц истинности

Суть метода состоит в фиксации условий задачи и полученных результатов рассуждений в специально составленных под задачу таблицах. В зависимости от того, является высказывание истинным или ложным, соответствующие ячейки таблицы заполняются знаками «+» и «-» либо «1» и «0».

Три спортсмена ( красный , синий и зеленый ) играли в баскетбол.
Когда мяч оказался в корзине, красный воскликнул: «Мяч забросил синий».
Синий возразил: «Мяч забросил зеленый».
Зеленый сказал: «Я не забрасывал».

Кто забросил мяч, если только один из троих сказал неправду?

Сначала таблицу составляют: слева записывают все утверждения, которые содержатся в условии, а сверху — возможные варианты ответа.

Затем таблицу последовательно заполняют: верные утверждения отмечают знаком «+», а ложные утверждения — знаком «-«.

Рассмотрим первый вариант ответа («мяч забросил красный «), проанализируем утверждения, записанные слева, и заполним первый столбик.
Исходя из нашего предположения («мяч забросил красный «), утверждение «мяч забросил синий» — ложь. Ставим в ячейке «-«.
Утверждение «мяч забросил зеленый» также ложь. Заполняем ячейку знаком «-«.
Утверждение зеленого «Я не забрасывал» – истина. Ставим в ячейке «+».

Рассмотрим второй вариант ответа (предположим, что мяч забросил зеленый ) и заполним второй столбик.
Утверждение «мяч забросил Синий» — ложь. Ставим в ячейке «-«.
Утверждение «мяч забросил зеленый « — истина. Заполняем ячейку знаком «+».
Утверждение зеленого «Я не забрасывал» – ложь. Ставим в ячейке «-«.

И, наконец, третий вариант: предположим, что «мяч забросил синий «.
Тогда утверждение «мяч забросил синий « — истина. Ставим в ячейке «+».
Утверждение «мяч забросил зеленый» — ложь. Заполняем ячейку знаком «-«. Утверждение зеленого «Я не забрасывал» – истина. Ставим в ячейке «+».

Так как по условию лишь один из троих ребят сказал неправду, в заполненной таблице выбираем такой вариант ответа, где будет только одно ложное утверждение (в столбце один знак «-«). Подходит третий столбец.

Значит, правильный ответ – мяч забросил синий.

Метод блок-схем

Метод блок-схем считается оптимальным вариантом для решения задач на взвешивание и на переливание жидкостей. Альтернативный способ решения этого типа задач — метод перебора вариантов — не всегда является оптимальным, да и назвать его системным довольно сложно.

• графически (блок-схемой) описываем последовательность выполнения операций;
• определяем порядок их выполнения;
• в таблице фиксируем текущие состояния.

Подробнее об этом и других способах решения логических задач с примерами и описанием хода решения мы рассказываем в полном Курсе ЛогикЛайк по развитию логического мышления.

Отгадывайте самые интересные загадки на логику, собранные специально для постоянных читателей нашего блога и учеников LogicLike, решайте логические задачи онлайн вместе с тысячами детей и взрослых!

Учим детей 5-12 лет решать любые логические и математические задачи. Более 3500 занимательных заданий с ответами и пояснениями.

Источник

От сложного к простому: алгоритм гарантированного решения любой задачи

Достаточно часто люди ставят перед собой задачи, но при этом не знают, как их решить. Каждый человек пытается самостоятельно найти решение данной проблемы. Программист Дэвид Макайвер делится своими методами решения сложных задач.

По мнению Макайвера, его система позволяет освоить то, что на первый взгляд является сложным. Для того чтобы добиться успеха в чем-либо Дэвид часто использует свою систему, но не всегда придерживается всех правил. Его система является беспроигрышной в любом случае, но время на выполнение задачи зависит от многих факторов. Суть данной системы заключается в том, что вы в любом случае получите определенную выгоду, даже если не достигнете конечной цели.

Система с одинарной петлей

Эта система подойдет тем, кто знает, что такое успех, но на данный момент он его не достиг. Как это работает:

1. Найдите легкую задачу, которая на первый взгляд кажется трудной.
2. Найдите что-то общее между легкой и трудной схожей задачей.
3. Продолжайте видоизменять задачу до тех пор, пока она не станет максимально простой.
4. Если вам не удалось превратить сложную задачу в простую, постарайтесь рассмотреть ее под другим углом. Также можно воспользоваться советом специалиста в определенной отрасли.
5. Если вам не удалось достичь желаемого, просто вернитесь ко второму пункту.

Данная система прекрасно работает благодаря отличному видению всего процесса обратной связи. Для того, чтобы становиться лучше в каком-то деле, необходимо сосредоточиться на одном аспекте, откинув все остальное. Обращая внимание сразу на несколько аспектов, вы упускаете возможность достичь успеха.

Петля двойная

В случае невозможности представления окончательного результата придется копнуть несколько глубже и провести двойную работу:

1. Сразу вам нужно воспользоваться предыдущей системой, чтобы лучше понять суть проблемы.
2. Примените одну петлю по отношению к проблеме, воспользовавшись своим чувством вкуса.
3. Обязательно получите отзыв со стороны о вашей проделанной работе.

Определение сложных точек

Часто понять то, что нужно улучшить, просто, однако, бывают ситуации, когда человек не может разобраться в данном вопросе. Чтобы лучше сориентироваться и увидеть очевидное, вам потребуется:

1. Максимально приложить усилия, чтобы выполнить задачу наилучшим образом. Не переживайте, если вас настигнет неудача, так как подобное явление бывает часто во многих начинаниях. В решении данного вопроса вам поможет список, где вы сможете указать, что сделали хорошо и плохо. Если вы не можете решить проблему, значит вам надо ознакомиться со списком и понять, где именно вы совершили ошибку.
2. Не пренебрегайте упражнениями в той области, которую вы начали изучать. Обратите внимание на то, что вам дается очень сложно.
3. Обратитесь за помощью к специалисту, который поможет вам разобраться с тем, в чем следует потренироваться.
4. Не стоит тратить время на простые задачи, лучше выбирайте сложные и старайтесь максимально их облегчить. Не бойтесь мыслить от простого к сложному и наоборот.

Пример решения задачи в написании

Научиться хорошо писать сложно, ведь этот процесс подразумевает множество пунктов, среди которых:

• процесс написания;
• поиск своего собственного стиля;
• невозможность начать из-за боязни насмешек со стороны окружающих;
• редактирование написанного.

Уже после упоминания этих основных моментов можно подумать и о менее важных. Что вам нужно:

• научиться печатать вслепую;
• использовать свой собственный голос, например, для записи текста на диктофон;
• не ожидать изначально от своих тестов высочайшего качества;
• не стараться отредактировать текст в целом, а лучше обращать внимание на конкретные вещи.

Существует немало примеров того, что следует попробовать, однако, для начала вам нужно выбрать исходную точку и следовать к своим целям. Четко поставленные цели и осознание необходимости их достижения – залог решения даже самых сложных задач. Курс Викиум «Целеполагание» как раз эффективно обучает постановке целей.

Источник