Выберите способы преобразования соответствующие рисункам

Способы преобразования чертежа

Способы преобразования чертежа служат для решения метрических задач по определению натуральной величины геометрических объектов (отрезка прямой или плоскости), либо кратчайшего расстояния между геометрическими объектами.

Суть этих способов заключается в том, что необходимо преобразовать комплексный чертеж так, чтобы рассматриваемый геометрический объект занял положение параллельное какой-либо плоскости проекций. Тогда на нее он, очевидно, спроецируется в натуральную величину.

Такое преобразование комплексного чертежа может быть осуществлено двумя основными способами:

1. Способом вращения, при котором оставляют неизменной систему плоскостей проекций, а меняют положение заданного геометрического объекта путем его вращения вокруг одной или последовательно вокруг двух подходящим образом выбранных осей так, чтобы интересующие нас прямые или плоскости оказались параллельными одной из плоскостей проекций. В качестве оси вращения обычно выбирают прямую, перпендикулярную одной из плоскостей проекций.

2. Способом замены плоскостей проекций, при котором оставляют неизменным положение в пространстве геометрического объекта, а заменяют одну или последовательно обе плоскости проекций так, чтобы интересующие нас прямые или плоскости оказались параллельными одной из новых плоскостей проекций.

Этими способами также можно решать задачи на приведение геометрических объектов в проецирующее положение.

Способ вращения вокруг проецирующей оси

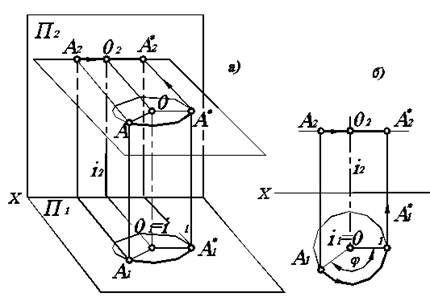
Рассмотрим вращение точки А вокруг оси i, перпендикулярной горизонтальной плоскости проекций П₁ (рис. 4.1). Ось вращения проецируется на плоскость П₁ в точку, а на плоскость П₂ — в прямую, перпендикулярную оси ОХ. Траекторией движения точки А будет окружность, лежащая в плоскости вращения, параллельной плоскости П₁, с центром вращения в точке О, лежащей на оси, и с радиусом вращения ОА (рис. 4.1, а).

Траектория движения точки проецируется на плоскость П₁ в натуральную величину, а на плоскость П₂ — в виде прямой, параллельной оси ОХ. Радиус окружности проецируется на плоскость П₁ в натуральную величину. Таким образом, горизонтальная проекция А₁ точки А движется по окружности, а фронтальная проекция А₂ — по прямой, параллельной оси ОХ.

Для того, чтобы повернуть точку А на угол j, откладывают этот угол на горизонтальной проекции (рис. 4.1, б) и получают горизонтальную проекцию А₁ точки А в новом положении А₁*. Фронтальную проекцию А₂* этой точки находят с помощью линии проекционной связи, которую проводят из точки А₁* до пересечения с прямой, проведенной из точки А₂ параллельно оси ОХ.

Рис. 4.1. Вращение точки вокруг горизонтально-проецирующей оси

Способ плоскопараллельного перемещения

Способ плоскопараллельного перемещения является частным случаем способа вращения вокруг проецирующей оси, с той лишь разницей, что геометрический объект можно не только вращать, но и перемещать вдоль плоскости, параллельной одной из плоскостей проекций.

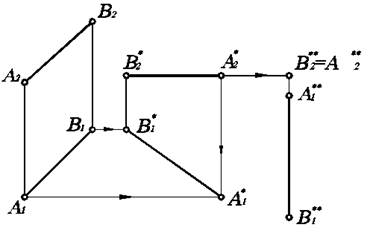
При перемещении отрезка прямой в новое положение таким образом, что его крайние точки движутся параллельно какой-либо плоскости проекций, длина проекции отрезка на эту плоскость остается неизменной (рис. 4.2).

Рис. 4.2. Плоскопараллельное перемещение отрезка прямой.

Преобразуем последовательно отрезок прямой линии общего положения АВ в положение горизонтали, затем фронтально-проецирующее положение. Для этого расположим фронтальную проекцию А₂В₂ отрезка АВ параллельно оси ОХ (А₂*В₂* параллелен ОХ) в любом месте чертежа. При этом точки А₁ и В₁ перемещаются в новое положение по прямым, параллельным оси ОХ, и будут лежать на линиях связи с А₂*, В₂* соответственно.

Тогда новая горизонтальная проекция займет положение А₁*В₁*. Очевидно, что А₁*В₁*- натуральная величина отрезка АВ, т.к. А*В* является горизонталью. Затем А₁*В₁* переместим в новое положение, чтобы А₁**В₁** была перпендикулярна оси ОХ. Тогда А₂** = В₂**, т.е. АВ займет положение проецирующей прямой. Следует заметить, что при определение натуральной величины АВ, которой является А₁*В₁*, удаленность проекции А₂*В₂* от оси ОХ не играет роли. Важно лишь выполнение двух требований: А₂*В₂* должна быть равна А₂В₂ и параллельна оси ОХ.

Способ замены плоскостей проекций

Способ замены плоскостей проекций состоит в том, что одна из основных плоскостей проекций П₁ или П₂ заменяется новой плоскостью проекций П₄, подходящим образом расположенной относительно изображаемого геометрического объекта, но перпендикулярной незаменяемой плоскости проекций.

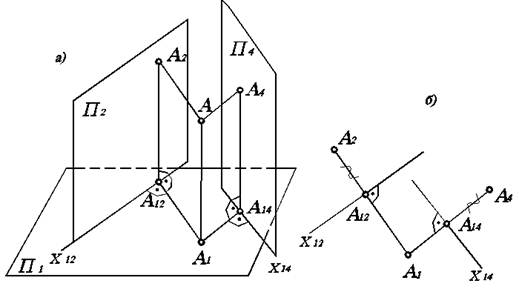
В результате замены одной из основных плоскостей на плоскость проекций П₄ получаем вместо старой системы плоскостей проекций П₁/П₂ новую систему П₁/П₄ (рис. 4.3), если заменялась плоскость П₂, и систему П₂/П₄, если заменялась плоскость П₁.

Рис. 4.3. Интерпретация способа замены плоскостей проекций

Например, на рис. 4.3а плоскость П₄ может выступать в роли фронтальной плоскости проекций П₂. На рисунке 4.3б, фигурными скобками отмечены расстояния от точки А до горизонтальной плоскости проекций П₁. Естественно, как видно на рис. 4.3а, эти расстояния равны А₂А₁₂ = А₄А₁₄, так как высота точки А над плоскостью П₁ проецируется как на П₂, так и на П₄ в виде одинаковых отрезков. Расстояние же до П₂ и П₄ от точки А могут быть различными, поэтому А₁А₁₂¹А₁А₁₄.

Способ замены плоскостей проекций рационально применять при решении следующих задач:

— определение натуральной величины отрезка прямой линии;

— определение натуральной величины плоской фигуры;

— определение натуральной величины двугранного угла;

— определение кратчайшего расстояния от точки до прямой линии или до плоскости;

— определение кратчайшего расстояния между двумя параллельными или двумя скрещивающимися прямыми.

Решение задач данным способом рассмотрим на нескольких примерах.

Определение длины отрезка общего положения

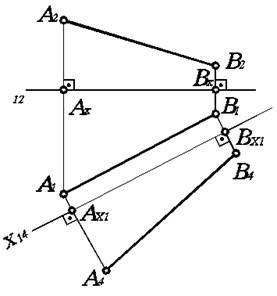
Для определения натуральной величины (длины) отрезка АВ прямой линии необходимо сделать этот отрезок прямой линии общего положения в новой системе плоскостей проекций линией уровня. Чтобы отрезок АВ стал линией уровня относительно новой плоскости проекций, заменим плоскость П₂ на плоскость П₄, параллельную АВ, и перейдем от системы П₁/П₂ к системе П₁/П₄. Новую ось проекций X₁₄, выбираем параллельно А₁В₁ (рис. 4.4). Для построения новой проекции отрезка АВ проводим новые линии проекционной связи перпендикулярно оси Х₁₄, и отмечаем на них новые проекции А₄, В₄ точек А и В. Для этого откладываем А_х1А₄ = А₂А_х, В_х1В₄ = В₂В_х.

Рис. 4.4. Преобразование прямой общего положения в прямую уровня.

Соединяя найденные точки А₄, В₄, получаем новую проекцию А₄В₄ отрезка АВ. Как видим, отрезок АВ в новой системе плоскостей проекций П₁/П₄ является линией уровня, так как А₁В₁ параллельна X₁₄, а следовательно, АВ параллельна П₄. Тогда, очевидно, что А₄В₄ является натуральной величиной отрезка АВ.

Определение натуральной величины плоской фигуры

Для определения натуральной величины плоской фигуры необходимо дополнительную плоскость построить так, чтобы она была параллельна рассматриваемой фигуре, и тогда на эту плоскость проекций плоская фигура спроецируется в натуральную величину. Если в качестве плоской фигуры выбрать треугольник, тогда задача формулируется следующим образом: преобразовать плоскость треугольника общего положения в новой системе плоскостей проекций в плоскость уровня.

Одной заменой плоскостей проекций эту задачу решить невозможно, так как необходимо соблюдать условие: новая плоскость должна быть перпендикулярна незаменяемой. Поэтому решим эту задачу двумя заменами: первой заменой введем плоскость, которая перпендикулярна треугольнику АВС, второй заменой – плоскость, параллельную треугольнику АВС.

Для того, чтобы построить плоскость П₄, перпендикулярную треугольнику АВС, необходимо расположить ее так, чтобы она была перпендикулярна фронтали либо горизонтали треугольника АВС.

Пусть П₄ перпендикулярна горизонтали, тогда новая ось Х₁₄ должна быть перпендикулярна h₁ (рис. 4.5).

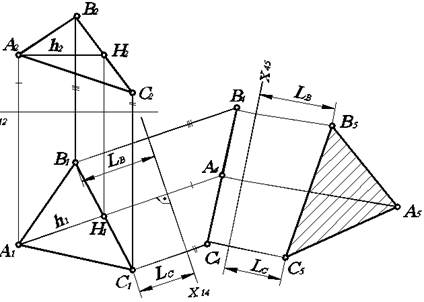
Рис. 4.5. Преобразование плоскости общего положения в плоскость уровня.

Построим ее на произвольном расстоянии от треугольника А₁В₁С₁. Затем из точек А₁, В₁, С₁ проведем линии связи перпендикулярно Х₁₄. На каждой из них от оси Х₁₄ отложим отрезок, равный расстоянию от фронтальной проекции соответствующей точки до оси Х₁₂. В результате получаем новую проекцию В₄А₄С₄ треугольника АВС, которая представляет собой прямую, поскольку плоскость треугольника АВС перпендикулярна плоскости П₄.

Второй заменой вводим вместо П₁ плоскость П₅, параллельную плоскости треугольника АВС. Тогда получается система плоскостей проекций П₄/П₅, ось Х₄₅ которой параллельна В₄А₄С₄. Она может быть расположена на произвольном расстоянии от В₄А₄С₄. Далее из точек В₄ А₄ С₄ проводим линии связи перпендикулярно Х₄₅, и на каждой из них от оси Х₄₅ откладываем отрезок, равный расстоянию от горизонтальной проекции соответствующей точки до оси Х₁₄. Получим точки А₅, В₅, С₅, соединив которые имеем треугольник А₅В₅С₅, который и является натуральной величиной треугольника АВС, поскольку в новой системе плоскостей проекций треугольник АВС параллелен плоскости П₅.

Вопросы для самоконтроля

1. С какой целью осуществляется преобразование комплексного чертежа?

2. В чем заключается способ вращения вокруг проецирующей оси?

3. Назовите основные способы преобразования комплексного чертежа?

4. В чем сущность способа плоскопараллельного перемещения.

5. В чем заключается способ замены плоскостей проекций?

Источник

Урок для 10 кл по предмету «Графика и проектирование» по теме «Преобразование формы предмета»

Раздел: Преобразование формы

ФИО учителя: Шаяхметова Л.А.

Тема : Преобразования формы предмет а

Учебные цели для достижения на этом уроке (ссылка на учебную программу)

10.5.1.1- Выполнять преобразование формы предмета методом выдавливания и удаления частей

Освоить способы сечения многогранников и тел вращения плоскостью различного положения, с последующим выполнением комплексного чертежа вновь полученной детали

Развивать пространственное воображение уч-ся

Продолжить формирование умений и навыков выполнения чертежа детали

Учащиеся освоят приемы и способы преобразования формы предмета путем удаления части предмета

Научатся построению комплексного чертежа преобразованного предмета

Уч-ся используют в речи ключевые термины и понятия по теме «Преобразования формы предмета» для развития языковых компетенций активно используют терминологию на трех языках

Ученик достиг цели если:

— организовал учебное сотрудничество с учителем и одноклассниками

— представляет процесс преобразования детали

— может выполнять практическую работу самостоятельно

— оценивает собственную работу и работу других

Общенациональная идея «Мәңгілік ел» Трудовое общество общее для всех

реализуется на операционном этапе при выполнении групповой работы.

Проявление уважения к другой точке зрения реализуется при обсуждении материала.

— проекции геометрических тел

Организационный момент, создание атмосферы в классе.

Выведение уч-ся на тему урока.

На учительском столе стоят геометрические тела. Необходимо их назвать.

Затем на стол поставить усеченные геометрические тела, со срезом, с вырезом.

Вопрос: — каким способом получены данные геометрические тела?

При конструировании часто возникает необходимость выполнять чертеж предмета, преобразовав, т.е. изменив его заданную форму. Преобразование формы предмета может осуществляться посредством удаления ее частей (вырез, срез), изменения их положения, наращивания, поворота и т.д.

Подведение итогов опроса и определение темы урока.

Сегодня мы рассмотрим преобразования, связанные с удалением частей предмета.

1.Построение чертежей предметов со срезами .

В практике часто встречаются детали, форма которых представляет собой геометрическое тело с плоскими срезами или с наклонными гранями (рис.) Срез — это результат сечения поверхности многогранника или тела вращения какой-либо плоскостью.

Фигура, полученная в результате сечения многогранника, — многоугольник. В сечении тела вращения плоскостью получаются фигуры, ограниченные кривыми или прямыми линиями в зависимости от того, как расположена в пространстве секущая плоскость относительно поверхности тела или плоскости проекций

Рассмотрим пример Слайд 2:

Очевидно, что призма такой формы получится в результате пересечения ее боковой поверхности плоскостью а», перпендикулярной фронтальной плоскости проекций.

Рассмотрим пример построения проекций фигуры сечения (рис. б.) Фронтальная проекция фигуры сечения совпадает с фронтальной проекцией секущей плоскости (линия 1″-2″-3″), горизонтальная — с горизонтальной проекцией основания призмы (1′-2’—3′).

Профильную проекцию фигуры сечения находим, исходя из свойств принадлежности точек фигуры сечения ребрам призмы (1″-2′»-3′» ). Их проекции строят с помощью линий связи.

В сечении цилиндра плоскостью могут получаться следующие фигуры: прямоугольник, круг, эллипс (Слайд 3). В первом случае секущая плоскость должна быть параллельна оси вращения цилиндра (рис. а), во втором — направлена перпендикулярно ей (рис. б), в третьем — наклонена к оси вращения под любым углом, не равным 90° (рис. в).

Какие фигуры получаются в результате сечения многогранника плоскостью?

Какие фигуры получаются в результате сечения цилиндра плоскостью?

Задание Слайд 8:. Постройте чертежи призмы, пирамиды, цилиндра и конуса, форма которых изменена в результате сечения плоскостями, перпендикулярными фронтальной плоскости проекций.

Чертежи должны содержать два или три вида (по заданию учителя). Лишние линии удалите.

Построение вырезов на геометрических телах Слайд 4.

В практике встречается много деталей и других предметов, геометрическая форма которых изменена различными вырезами. Чтобы выполнить или прочитать чертеж такого предмета, нужно представить его первоначальную форму и форму выреза.

Рассмотрим пример Слайд 5.

На рисунке а дан чертеж пробки. Изучив его, устанавливаем, что деталь изготовлена из заготовки цилиндрической формы, в которой сделан вырез прямоугольной формы (рис.).

Чтобы построить вид сверху детали, сначала изображают прямоугольник — вид цилиндра сверху, являющийся исходной формой детали. Затем строят проекцию выреза. Обозначим некоторые характерные точки (А», B» и А'» = B'»), которые определяют проекции выреза, и по ним с помощью линий связи построим горизонтальные проекции А’, B’ этих точек и им симметричных (рис.).

Установив форму выреза, легко решить, какие линии на виде сверху надо обводить сплошными толстыми основными, какие — штриховыми линиями, а какие — удалить.

Задание Слайд 9. Постройте чертежи призмы и цилиндра, форма которых изменена вырезами. Чертеж должен содержать три вида (рис. а и б).

Задание Слайд 10. Работа в парах.

Нарисуйте части детали (рис.), удаленные посредством вырезов. Сколько их? Постройте вид сверху детали.

Учитель анализирует работу учащихся, и дает комментарии по поводу их работы на уроке.

Особое внимание обращается на то, как работали учащиеся в парах.

Презентация «Преобразование формы предмета методом сечения плоскостью и срезом»

— что узнали нового?

— в чем заключались трудности при построении чертежа преобразованной детали?

Используя стратегию «Две звезды, одно пожелание» получить обратную связь от учащихся.

Домашнее задание: повторить изученный материал, дочертить задание.

Источник