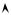Вторым способом задания закона распределения случайной величины является
1. Формирование представление о случайной величине, дискретных и непрерывных случайных величинах.
2. Знакомство с законом распределения дискретной случайной величины, функцией распределения и плотностью распределения непрерывной случайной величины, числовых характеристиках случайных величин.
1. Виды случайных величин.
2. Закон распределения дискретной случайной величины.
3. Функция распределения вероятностей случайной величины.
4. Плотность распределения вероятностей непрерывной случайной величины.
5. Математическое ожидание.
6. Дисперсия и среднеквадратическое отклонение.
1. Виды случайных величин.
Случайной величиной называется такая величина, которая случайно принимает какое-то значение из множества возможных значений.
Случайные величины обозначаются: X , Y , Z . Значения, которые они принимают: x , y , z .
По множеству возможных значений различают дискретные и непрерывные случайные величины.
Дискретными называются случайные величины, значениями которых являются только отдельные точки числовой оси. (Число их может быть как конечно, так и бесконечно).
Пример: Число родившихся девочек среди ста новорожденных за последний месяц- это дискретная случайная величина, которая может принимать значения 1,2,3,…
Непрерывными называются случайные величины, которые могут принимать все значения из некоторого числового промежутка.
Пример: Расстояние, которое пролетит снаряд при выстреле- это непрерывная случайная величина, значения которой принадлежат некоторому промежутку [а; в].
2. Закон распределения дискретной случайной величины.
Дискретную случайную величину Х можно характеризовать законом распределения .
Закон распределения дискретной случайной величины— это соответствие между возможными значениями случайной величины и их вероятностями.
Закон распределения можно задать таблично, аналитически, графически.
При задании закона распределения таблично, в первую строку таблицы вносятся возможные значения случайно величины, а во вторую- их вероятности.
Пример: Монету подбросили 3 раза. Запишите закон распределения числа выпадения «герба».
Возможные значения данной случайной величины: 0, 1, 2, 3.
Найдем вероятность того, что «герб» не появится (0 раз).
Найдем вероятность того, что «герб» появится 1 раз.
Найдем вероятность того, что «герб» появится 2 раза.
Найдем вероятность того, что «герб» появится 3 раза.
Тогда закон распределения данной дискретной случайной величины можно представить таблицей:
Для наглядности закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки с координатами (xi ; pi), а затем соединяют их отрезками прямых. Полученная фигура называется многоугольником распределения.
Однако, такой способ задания (перечисление всех возможных значений случайной величины и их вероятностей) не подходит для непрерывных случайных величин. Составить перечень их возможных значений невозможно.
3. Функция распределения вероятностей случайной величины.
Дадим новый способ задания любых типов случайных величин. С этой целью введем функцию распределения вероятностей случайной величины.
Функцией распределения случайной величины называют функцию F ( x ), определяющую вероятность того, что случайная величина Х в результате испытания примет значение меньшее х, т.е. F ( x ) P ( X x ).
Геометрически это равенство можно истолковать так: F ( x ) –есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Иногда вместо термина «функция распределения» используется термин «интегральная функция».
Свойства функции распределения:
Свойство 1: Значения функции распределения принадлежат интервалу [0; 1]: .
Свойство 2: F ( x )- неубывающая функция, т.е. при .
Следствие 1: Вероятность того, что случайная величина примет значение, заключенное в интервале (а; b ), равна приращению функции распределения на этом интервале:
Пример: Случайная величина Х задана функцией распределения:
Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0; 2).
Свойство 3: Если возможные значения случайной величины принадлежат интервалу ( a ; b ), то F ( x )=0 при (т.к. ; F ( x )=1 при (т.к. — достоверное событие.
Следствие: Если возможные значения непрерывной случайной величины распределены на всей числовой оси, то справедливы следующие предельные соотношения:
Рассмотренные выше свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.
График расположен в полосе, ограниченной прямыми у=0, у=1 (1 свойство).
4. При возрастании значения х в интервале ( a ; b ), в котором заключены все возможные значения случайной величины, график растет вверх (2 свойство).
5. При ординаты графика равны 0, при ординаты графика равны 1 (3 свойство).
Замечание: График функции распределения дискретной случайной величины имеет ступенчатый вид.
Пример: Дискретная случайная величина Х задана таблицей распределения:
Найдите функцию распределения и постройте ее график.
Решение: Если , то F ( x )=0 по 3 свойству. Если , то F ( x )= P ( X Если , то F ( x )= P ( X Если х>8, то F ( x )=1. Действительно, событие Х
Итак, функция распределения имеет следующий вид:
4. Плотность распределения вероятностей непрерывной случайной величины.
Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (дифференциальной функцией).
Плотность распределения вероятностей непрерывной случайной величины Х называют функцию f ( x )- первую производную от функции распределения F ( x ).
Теорема: Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу ( a ; b ), равна определенному интегралу от плотности распределения, взятому в пределах от а до b .
Пример: Задана плотность вероятностей случайной величины Х.
Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).
Свойства плотности распределения вероятностей:
Свойство 1: Плотность распределения- неотрицательная функция: f ( x ) > 0.
Свойство 2: Несобственный интеграл от плотности распределения в пределах от равен 1: .
Геометрический смысл этого свойства заключается в следующем: площадь криволинейной трапеции, ограниченной осью ОХ и кривой распределения, равна 1. В частности, если все возможные значения случайной величины принадлежат интервалу ( a ; b ), то .
Часто, для того чтобы характеризовать случайную величину используют числа, которые описывают случайную величину суммарно. Такие числа называются числовыми характеристиками случайной величины. К числу важнейших числовых характеристик относятся математическое ожидание и дисперсия.
5. Математическое ожидание.
Математическое ожидание приближенно равно среднему значению случайной величины. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и следовательно стреляет лучше.
Математическое ожидание дискретной случайной величины Х- это величина , где xi— значения случайной величины, pi— их вероятности, n — число возможных значений случайной величины.
Пример: Найдите математическое ожидание, зная закон распределения дискретной случайной величины.
Источник
2.2 Закон распределения случайной величины
Очевидно, что для полного описания исследуемого вероятностного эксперимента (то есть для исчерпывающего задания характеризующей его случайной величины) недостаточно задать только пространство элементарных событий Ω . К этому необходимо добавить также:
а) для дискретной случайной величины — правило, сопоставляющее каждому возможному значению случайной величины х i вероятность того, что случайная величина X примет в результате эксперимента это значение:
б) для непрерывной случайной величины – правило, позволяющее поставить в соответствие любой измеримой области ∆ X возможных значений случайной величины X вероятность попадания значения случайной величины в эту область:
Дадим общее определение: законом распределения случайной величины X называется любое соотношение, устанавливающее связь между возможными значениями этой случайной величины и соответствующими им вероятностями.
2.2.1 Ряд распределения
Пусть X – дискретная случайная величина, а x 1 , x 2 , x 3 ,… – ее значения. Совокупность всех элементарных событий, на которых X принимает фиксированное значение x i , образует событие X = x i .
Простейшим способом задания закона распределения дискретной случайной величины является ряд распределения . Это таблица, в первой строке которой указаны возможные значения случайной величины x 1 , x 2 , x 3 , …, а во второй – соответствующие им вероятности p 1 , p 2 , p 3 ,…, где p i = P ( X = x i ) –
вероятность того, что в результате эксперимента случайная величина X примет значение x i :
Так как события ( X = x 1 ), ( X = x 2 ),… – несовместны, и их объединение
представляет собой все пространство элементарных событий, то сумма веро-
ятностей р i равна 1:
∑ P ( X = x i ) = ∑ p i = 1.
Эта единица как-то распределена между различными значениями случайной величины. Отсюда и термин «распределение».
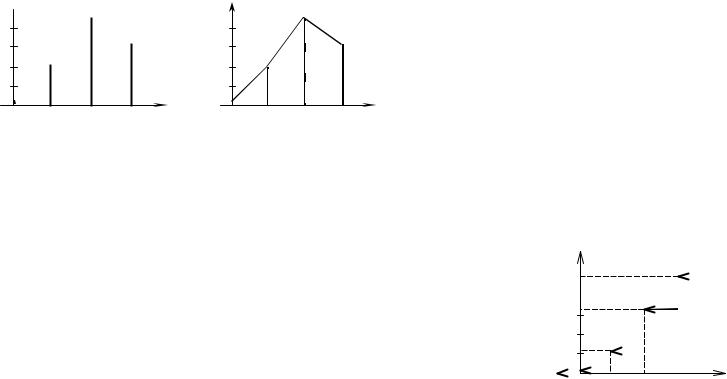
Графическое изображение ряда распределения может быть представ-
лено одним из двух способов: в виде столбцовой диаграммы и в виде многоугольника распределения.
Столбцовая диаграмма строится следующим образом: для каждого возможного значения случайной величины восстанавливается перпендикуляр к оси абсцисс, на котором откладывается вероятность данного значения.
При построении многоугольника распределения по оси абсцисс откладываются возможные значения случайной величины, по оси ординат – соответствующие им вероятности, и полученные соседние точки соединяются отрезками.
Пример 14. Рассматривается работа трех функционирующих независимо друг от друга технических устройств (ТУ). Вероятности безотказной работы в течение заданного интервала времени t для каждого из ТУ соответственно равны: 0,6, 0,7 и 0,75. Рассматривается случайная величина X – число ТУ, проработавших безотказно в течение времени t . Построить ряд распределения этой случайной величины.
Решение. Возможные значения данной случайной величины: 0, 1, 2, 3. Запишем их в верхней строке ряда распределения. Для определения вероятностей возможных значений данной случайной величины введем в рассмотрение события: A i – <безотказная работа в течение времени t i -го устройства>, i = 1, 2, 3. B j – <безотказная работа j устройств в течение времени t >, j = 0, 1, 2, 3. События B j можно представить в виде
B 0 = A 1 ∩ A 2 ∩ A 3 ;
B 1 = A 1 ∩ A 2 ∩ A 3 A 1 ∩ A 2 ∩ A 3 A 1 ∩ A 2 ∩ A 3 ;
B 2 = A 1 ∩ A 2 ∩ A 3 A 1 ∩ A 2 ∩ A 3 A 1 ∩ A 2 ∩ A 3 ; B 3 = A 1 ∩ A 2 ∩ A 3 .
Применяя теорему сложения вероятностей несовместных событий и теорему умножения вероятностей независимых событий, вычисляем:
P ( X = 0) = P ( B 0 ) = P ( Ā 1 ) P ( Ā 2 ) P ( Ā 3 ) = 0,4 0,3 0,25 = 0,03;
P ( X = 1) = P ( B 1 ) = P ( A 1 ) P ( Ā 2 ) P ( Ā 3 ) + P ( Ā 1 ) P ( A 2 ) P ( Ā 3 ) + P ( Ā 1 ) P ( Ā 2 ) P ( A 3 ) = = 0,6 0,3 0,25 + 0,4 0,7 0,25 + 0,4 0,3 0,75 = 0,205;
P ( X = 2) = P ( B 2 ) = P ( A 1 ) P ( A 2 ) P ( Ā 3 ) + P ( A 1 ) P ( Ā 2 ) P ( A 3 ) + P ( Ā 1 ) P ( A 2 ) P ( А 3 ) = = 0,6 0,7 0,25 + 0,6 0,3 0,75 + 0,4 0,7 0,75 = 0,45;
P ( X = 3) = P ( B 3 ) = P ( A 1 ) P ( A 2 ) P ( A 3 ) = 0,6 0,7 0,75 = 0,315.
Таким образом, ряд распределения случайной величины X имеет вид
Убедимся, что ∑ p i = ∑ P ( X = x i ) = 1.
Столбцовая диаграмма и многоугольник распределения, представляющие ряд распределения этой случайной величины, изображены, соответственно, на рисунках 3 и 4.
P i
2.2.2 Функция распределения
Универсальным способом задания закона распределения, пригодным как для дискретных, так и для непрерывных случайных величин, является функция распределения.
Функцией распределения случайной величины X называется функция
F ( x ), определяющая для каждого значения x вероятность того, что случайная величина X примет значение меньшее, чем x , то есть
Основные свойства функции распределения F ( x ) :
1. Так как по определению F ( x ) равна вероятности события, все возможные значения функции распределения принадлежат отрезку [0; 1]:
2. F ( x ) – неубывающая функция своего аргумента.
3. Вероятность того, что случайная величина примет значение, принад-
лежащее полуинтервалу [ a , b ), равна приращению функции распределения на этом интервале
P ( a ≤ X b ) = F ( b ) – F ( a ).
4. Если все возможные значения случайной величины принадлежат отрезку [ a , b ], то
F ( x ) = 0, при x ≤ a ; F ( x ) = 1, при x > b .
Функция распределения дискретных случайных величин может быть определена по формуле
F ( x ) = ∑ P ( X = x i ) .
Если известен ряд распределения дискретной случайной величины, легко построить ее функцию распределения. Продемонстрируем, как это делается на примере 14.
Пример 14. Ряд распределения случайной величины X , обозначающей число устройств, проработавших безотказно в течение времени t , имеет вид
Определим значения функции F ( x ) = P ( X x ) для всех возможных значений x : при x (– ∞ , 0] нет ни одного значения случайной величины X , меньшего данных
значений x , то есть нет ни одного слагаемого в сумме (6): F ( x ) = 0;
при x (0; 1] только одно возможное значение ( X = 0) меньше рассматриваемых значений x . То есть при x (0; 1] F ( x ) = P ( X = 0) = 0,03;
при x (1, 2] два значения ( X = 0 и X = 1) меньше данных значений x , следователь-
но, F ( x ) = P ( X = 0) + P ( X = 1) = 0,03 + 0,205 = 0,235;
при x (2, 3] F ( x ) = P ( X = 0) + P ( X = 1) + P ( X = 2) = 0,03 + 0,205 + 0,45 = 0,685 ;
при x (3, ∞ ) все возможные значения случайной величины X будут меньше дан-
и F ( x ) = P ( X = 0) + P ( X = 1) + P ( X = 2) + P ( X = 3) = 0,03 + 0,205 +
График функции F ( x ) изображен на ри-
В общем случае, функция распределения F ( x ) дискретной случайной величины X есть разрывная ступенчатая функция, непрерывная слева, скачки которой происходят в точках, соответствующих возможным значениям х 1 , х 2 , … случайной величины X и равны вероятностям p 1, p 2, … этих значений.
Функция распределения непрерывных случайных величин. Теперь можно дать более точное определение непрерывных случайных величин: случайная величина X называется непрерывной , если ее функция распределения F ( x ) при всех значениях x непрерывна и, кроме того, имеет производную F ′ ( x ) всюду, за исключением, может быть, отдельных точек.
(На рисунках 13, 15 и 17 (разд. 2.4) изображены графики функций распределения непрерывных случайных величин, подчиняющихся равномерному, показательному и нормальному законам).
Из непрерывности функции F ( x ) следует, что вероятность каждого от-
дельного значения непрерывной случайной величины равна нулю .
Из равенства нулю вероятности P ( X = x 1 ) не следует, что событие ( X = х 1 ) невозможно. В результате испытания случайная величина обязательно примет одно из своих возможных значений. В частности, это значение может оказаться равным х 1 .
Аксиому сложения вероятностей несовместных событий ввели только для конечного и счетного множеств событий; для несчетного множества она попросту несправедлива. Вероятность попадания случайной величины на участок от a до b равна сумме вероятностей попадания на элементарные участки, образующие его, как бы малы эти участки ни были, но не равна сумме вероятностей попадания в отдельные точки.
Представление о событии, имеющем отличную от нуля вероятность, но складывающемся из событий с нулевой вероятностью, не более парадоксально, чем, например, представление о фигуре, имеющей определенную площадь, в то время как ни одна точка внутри фигуры, отличной от нуля площадью не обладает; или представление о массе некоторого тела, состоящего из материальных точек, каждая из которых обладает нулевой массой.
Так как вероятность каждого отдельного значения непрерывной случайной величины равна 0, свойство 3 функции распределения для непрерывной случайной величины будет иметь вид
P ( a ≤ X b ) = P ( a ≤ X ≤ b ) = P ( a X ≤ b ) = P ( a X b ) = F ( b ) – F ( a ).
Пример 15. Производится выстрел по мишени, имеющей форму круга радиуса R . Случайная величина X – расстояние от точки попадания до центра мишени. Определить закон распределения этой случайной величины. Найти вероятность попадания в центральный круг мишени радиуса R /3.
Решение. Все возможные значения случайной величины X принадлежат отрезку [0; R ]. Следовательно, при x (– ∞ , 0) нет ни одного значения случайной величины X , меньшего данных значений x , то есть F ( x ) = 0. При x ( R , ∞ ) все значения случайной величины будут меньше данных значений x , следовательно, F ( x ) = 1. Для определения F ( x ) = P ( X x ) при x [0; R ] обратимся к рисунку 6.
Вероятность события ( X x ) равна вероятности попадания в круг радиуса x , при
условии, что попадание в круг радиуса R (то есть попадание в мишень) – достоверное
событие. Используя геометрический метод определения вероятности, вероятность
попадания в круг радиуса x можно определить как отноше-
ние площади круга радиуса x к площади круга радиуса R .
x [0; R ]: F ( x ) = P ( X x ) = ( π x 2 )/( π R 2 ) = x 2 / R 2 .
Источник